2023-2024学年人教版初中数学九年级下册 28.2 解直角三角形及其应用同步分层训练基础题

试卷更新日期：2024-03-20 类型：同步测试

进入出卷网下载

一、选择题

1. 在等腰△ABC中，AB=AC=4，BC=6，那么cosB的值是

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
2. 如图，商用手扶梯 $A B$ 的坡比为 $1 ： \sqrt{3}$ ，已知扶梯的长 $A B$ 为12米，则小明乘坐扶梯从 $B$ 处到 $A$ 处上升的高度 $A C$ 为（）

A、6米 B、 $6 \sqrt{3}$ 米 C、12米 D、 $12 \sqrt{3}$ 米

查看试题解析
3. 小明从学校出发，步行去少年宫（如图），行走路线正确的是（）

A、向南偏东300行走600米 B、向南偏西50°行走600米 C、向南偏东600行走600米 D、向南偏西40行走600米

查看试题解析
4. 某中学九年级数学兴趣小组的同学准备测量校内旗杆 $A B$ 的高度，他们在 $C$ 点测得旗杆顶端 $A$ 的仰角 $∠ B C A = 30 °$ ，向前走了30米到达 $D$ 点，在 $D$ 点测得旗杆顶端A的仰角 $∠ B D A = 60 °$ ，则旗杆 $A B$ 的高为多少米？（）

A、15米 B、 $15 \sqrt{3}$ 米 C、 $15 \sqrt{2}$ 米 D、 $15 \sqrt{5}$ 米

查看试题解析
5. 在种植树木时，负责人员要求株距（相邻两树间的水平距离）为4m.如图，若在坡比为1∶2的山坡上种树，那么相邻两树间的坡面距离为（）

A、2 $\sqrt{5}$ m B、4m C、8m D、4 $\sqrt{5}$ m

查看试题解析
6. 如图，一只正方体箱子沿着斜面CD向上运动，∠C=α，箱高AB=1米.当BC=2米时，点A离地面CE的距离是多少米？（）

A、 $\frac{1}{c o s α} + \frac{2}{s i n α}$ B、 $\frac{1}{c o s α} + \frac{1}{2 s i n α}$ C、 $c o s α + 2 s i n α$ D、 $2 c o s α + s i n α$

查看试题解析
7. 如图，一艘轮船航行至O点时，测得某灯塔A位于它的北偏东40°方向，且它与灯塔A相距13海里，继续沿正东方向航行，航行至点B处时，测得灯塔A恰好在它的正北方向，则 $A B$ 的距离可表示为（）

A、 $13 c o s 40 °$ 海里 B、 $13 s i n 40 °$ 海里 C、 $\frac{13}{s i n 50 °}$ 海里 D、 $\frac{13}{c o s 50 °}$ 海里

查看试题解析
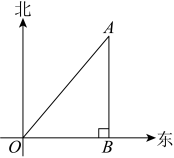8. 如图是某商场自动扶梯的示意图，自动扶梯 $A B$ 的坡角（ $∠ B A C$ ）为 $30.5 °$ ，乘客从扶梯底端升到顶端上升的高度 $B C$ 为5米，则自动扶梯 $A B$ 的长为（）

A、 $5 t a n 30.5 °$ 米 B、 $5 s i n 30.5 °$ 米 C、 $\frac{5}{s i n 30.5 °}$ 米 D、 $\frac{5}{c o s 30.5 °}$ 米

查看试题解析

二、填空题

9. 如图，某地修建的一座建筑物的截面图的高 $B C = 5 m$ ，坡面AB的坡度为 $1 ： \sqrt{3}$ ，则AB的长度为。

查看试题解析
10. 如图，飞机在目标B的正上方A处，飞行员测得地面目标C的俯角α=30°，如果地面目标B、C之间的距离为6千米，那么飞机离地面的高度AB等于千米．（结果保留根号）

查看试题解析
11. 如图，桔棒是一种原始的汲水工具，它是在一根竖立的架子上加上一根细长的杠杆，末端悬挂一重物，前端悬挂水桶.当人把水桶放入水中打满水以后，由于杠杆末端的重力作用，便能轻易把水提升至所需处，若已知：杠杆AB=6m，AO：OB=2∶1，支架OM⊥EF，OM=3m，AB可以绕着点О自由旋转，当点A旋转到如图所示位置时，∠AOM=45°，此时点B到水平地面EF的距离为m（结果保留根号）.

查看试题解析
12. 如图，小明将测倾器安放在与旗杆 $A B$ 底部相距 $6 m$ 的 $C$ 处，量出测倾器的高度 $C D = 1 m$ ，测得旗杆顶端 $B$ 的仰角 $α = 60 °$ ，则旗杆 $A B$ 的高度为m.（结果保留根号）

查看试题解析
13. 如图，△ABC是面积为的等边三角形，△ADE∽△ABC，AB=2AD，∠BAD=45°，AC与DE相交于点F，则△AEF的面积是.

查看试题解析

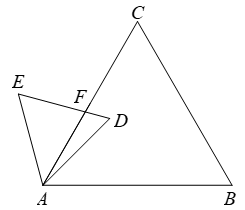
三、解答题

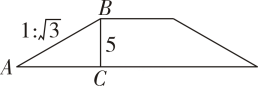
14. 如图，扶梯 AB的坡比为1： $\sqrt{3}$ ，滑梯CD的坡比为1：2，BE⊥AD于点E，CF⊥AD于点F，BE=CF.若FD=4m，BC=2m，某人从扶梯上去，经过顶部 BC，再沿滑梯滑下，他共经过多少路程(结果精确到 $0.1 m \sqrt{2} \approx 1.41 \sqrt{3} \approx 1.73 ， \sqrt{5} \approx 2.24) ?$

查看试题解析
15. 如图1，某款线上教学设备由底座，支撑臂 $A B$ ，连杆 $B C$ ，悬臂 $C D$ 和安装在 $D$ 处的摄像头组成．如图2是该款设备放置在水平桌面上的示意图，已知支撑臂 $A B ⊥ l$ ， $A B = 18 c m ， B C = 40 c m ， C D = 44 c m$ ，固定 $∠ A B C = 14 8^{°}$ ，可通过调试悬臂 $C D$ 与连杆 $B C$ 的夹角提高拍摄效果．

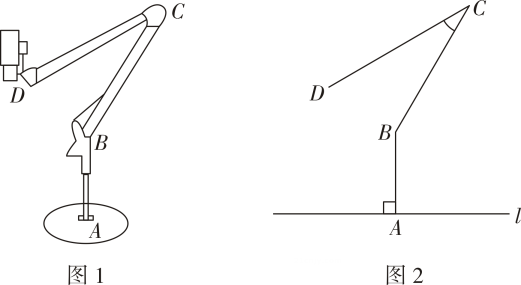(1)、当悬臂 $C D$ 与桌面 $l$ 平行时， $∠ B C D$ ＝°

(2)、问悬臂端点 $C$ 到桌面 $l$ 的距离约为多少?

(3)、已知摄像头点 $D$ 到桌面 $l$ 的距离为30cm时拍摄效果较好，那么此时悬臂 $C D$ 与连杆 $B C$ 的夹角 $∠ B C D$ 的度数约为多少?（参考数据： $s i n 5 8^{°} \approx 0.85 ， c o s 5 8^{°} \approx 0.53 ， t a n 5 8^{°} \approx 1.60$ ）

查看试题解析

四、综合题

16. 每年的11月9日是我国的“全国消防安全教育宣传日”，为了提升全民防灾减灾意识，某消防大队进行了消防演习．如图1，架在消防车上的云梯AB可伸缩（最长可伸至20m），且可绕点B转动，其底部B离地面的距离BC为2m，当云梯顶端A在建筑物EF所在直线上时，底部B到EF的距离BD为9m．

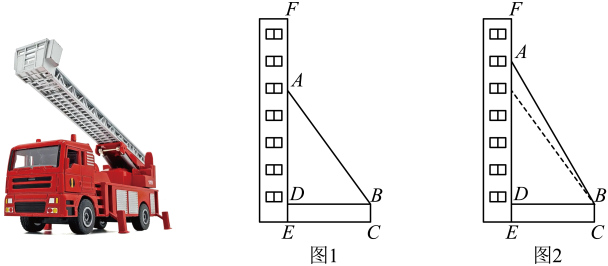(1)、若∠ABD=53°，求此时云梯AB的长．

(2)、如图2，若在建筑物底部E的正上方19m处突发险情，请问在该消防车不移动位置的前提下，云梯能否伸到险情处？请说明理由．（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3）

查看试题解析
17. $2022$ 年 $11$ 月 $9$ 日是我国第 $31$ 个“全国消防宣传日”，该年“ $119$ 消防宣传月”活动的主题是“落实消防责任，防范安全风险”．为落实该主题，济南市消防大队到建东小区进行消防演习．已知，图1是一辆登高云梯消防车的实物图，图2是其工作示意图，起重臂 $A C$ 可伸缩（ $15 m \leq A C \leq 26 m$ ），且起重臂 $A C$ 可绕点A在一定范围内转动，张角为 $∠ C A E$ （ $90 ° \leq ∠ C A E \geq 150 °$ ），转动点A距离地面 $B D$ 的高度 $A E$ 为 $3 m$ ．

(1)、当起重臂 $A C$ 长度为 $20 m$ ，张角 $∠ C A E = 127 °$ ，求云梯消防车最高点C距离地面 $B D$
的高度 $C F$ ；

(2)、已知该小区层高为 $2.8 m$ ，若某居民家突发险情，请问该消防车有效救援能达到几层？请说明理由．（结果精确到 $0.1 m$ ，参考数据： $s i n 37 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析

2023-2024学年人教版初中数学九年级下册 28.2 解直角三角形及其应用同步分层训练 基础题

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年人教版初中数学九年级下册 28.2 解直角三角形及其应用同步分层训练基础题