人教版数学九年级下册 28.1 锐角三角函数同步分层训练 培优题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 已知在中, , , , 则等于( )A、6 B、16 C、12 D、4
-
2. 在锐角中,=0,则( )A、 B、 C、 D、
-
3. 如图,在等腰中,于点 , 则的值( )
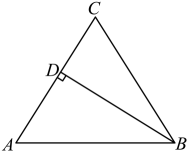 A、 B、 C、 D、
A、 B、 C、 D、 -
4. 正方形网格中,∠AOB如图放置,则sin∠AOB的值为( )
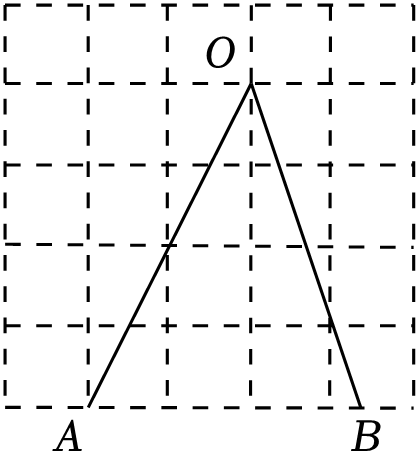 A、 B、 C、1 D、
A、 B、 C、1 D、 -
5. 如图,在中, , 是斜边上的中线, , , 则的值是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6. 如图,在△ABC中,∠ACB=90°,D是AB的中点,若CD=5,AC=8,则tanA=( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )
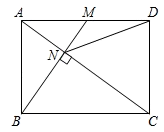 A、①②③④ B、①②③ C、①②④ D、②③④
A、①②③④ B、①②③ C、①②④ D、②③④ -
8. 如图,在矩形中, , , 将沿射线平移a个单位长度()得到 , 连接 , , 则当是直角三角形时,a的值为( )
 A、或 B、2或 C、或 D、或3
A、或 B、2或 C、或 D、或3
二、填空题
-
9. 在中,的对边分别为a、b、c,且满足 , 则的值为 .
-
10. 如图,在中, , 是的中点, , 交于 , 若 , 则.

-
11. 已知抛物线与直线只有一个交点,则锐角度.
-
12. 如图,在中, , 的中垂线交于点D , 交于点E , 若 , , 则的正切值为 .

-
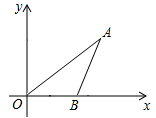
13. 如图,已知点坐标为 , 为轴正半轴上一动点,则度数为 , 在点运动的过程中的最小值为 .
三、解答题
-
14. 如图,是的直径,点在上,点为的中点,过点作的切线,交延长线于点 , 连接交于点 .
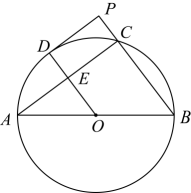 (1)、求证:四边形是矩形;(2)、作射线交的延长线于点F , 若 , , 求的长.
(1)、求证:四边形是矩形;(2)、作射线交的延长线于点F , 若 , , 求的长. -
15. 在中,是钝角,交BC的延长线于点D,E,分别为AC,AB的中点,.连结DF,EF,设DF与EC交于点.
 (1)、求证:.(2)、若时,求AC的长.
(1)、求证:.(2)、若时,求AC的长.
四、综合题
-
16. 如图,在中, , , .点D和点E分别为AC和BC的中点,连接DE.点P从点A出发,以每秒3个单位长度的速度沿AB向终点B运动,过点P作 , 交折线AC-CB于点F , 以PF为一边向PF的右侧作正方形PFGH.设点P的运动时间为t秒.
 (1)、DE的长为;(2)、当点F在AC边上,且时,求t的值;(3)、当点E落在正方形PFGH的内部时,求t的取值范围;(4)、当线段DE将正方形PFGH的边PF分成两部分的比为时,直接写出t的值.
(1)、DE的长为;(2)、当点F在AC边上,且时,求t的值;(3)、当点E落在正方形PFGH的内部时,求t的取值范围;(4)、当线段DE将正方形PFGH的边PF分成两部分的比为时,直接写出t的值. -
17. 如图,在矩形ABCD中,AB=2,BC=4,点E在直线AB上,连结DE,过点A作AF⊥DE交直线BC于点F,以AE、AF为邻边作平行四边形AEGF.直线DG交直线AB于点H.
 (1)、当点E在线段AB上时,求证:△ABF ∽△DAE.(2)、当AE=2时,求EH的长.(3)、在点E的运动过程中,是否存在某一位置,使得△EGH为等腰三角形.若存在,求AE的长.
(1)、当点E在线段AB上时,求证:△ABF ∽△DAE.(2)、当AE=2时,求EH的长.(3)、在点E的运动过程中,是否存在某一位置,使得△EGH为等腰三角形.若存在,求AE的长.
