人教版数学九年级下册 28.1 锐角三角函数同步分层训练 提升题
试卷更新日期:2024-03-20 类型:同步测试
一、选择题
-
1. 如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值为( )
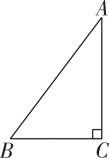 A、 B、 C、 D、2. 已知α为锐角,且 , 则α等于( )A、70° B、60° C、40° D、30°3. 等腰三角形的底边长为 , 周长为 , 则底角的正切值是( )A、 B、 C、 D、无法确定4. 如图,在 , , 延长到点 , 使 , 连接 , 若 , 则的值是( )
A、 B、 C、 D、2. 已知α为锐角,且 , 则α等于( )A、70° B、60° C、40° D、30°3. 等腰三角形的底边长为 , 周长为 , 则底角的正切值是( )A、 B、 C、 D、无法确定4. 如图,在 , , 延长到点 , 使 , 连接 , 若 , 则的值是( ) A、 B、1 C、 D、5. 如图,的顶点是正方形方格的格点,则的值为( )
A、 B、1 C、 D、5. 如图,的顶点是正方形方格的格点,则的值为( ) A、 B、3 C、 D、6. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC, , BC=44cm,则高AD约为( )(参考数据: , , )
A、 B、3 C、 D、6. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC, , BC=44cm,则高AD约为( )(参考数据: , , )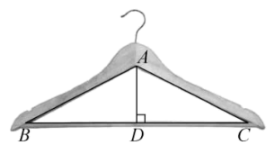 A、9.90cm B、11.22cm C、19.58cm D、22.44cm7. 在中,若 , 则的度数是( )A、 B、 C、 D、8. 如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )。
A、9.90cm B、11.22cm C、19.58cm D、22.44cm7. 在中,若 , 则的度数是( )A、 B、 C、 D、8. 如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )。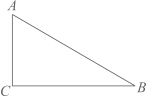 A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB
A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB二、填空题
-
9. 在中, , , , 则的面积为.10. 在中,若 , 满足 , 则 .11. 如图,在△ABC中,∠C=90°,AC=6,BC=3,边AB的垂直平分线交AC边于点D,交AB边于点E,连接DB,那么∠的值是 .
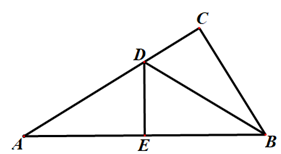 12. 如图,在平面直角坐标系内有一点 , 那么与轴正半轴的夹角的正弦值 .
12. 如图,在平面直角坐标系内有一点 , 那么与轴正半轴的夹角的正弦值 . 13. 如图,在中, , 分别以和为边向外作正方形和正方形 , 过点作的延长线的垂线,垂足为点 . 连接 , 交的延长线于点 . 下列说法:①;②若 , , 则;③;④;⑤若 , , 则的面积为 , 正确的有 . (填序号)
13. 如图,在中, , 分别以和为边向外作正方形和正方形 , 过点作的延长线的垂线,垂足为点 . 连接 , 交的延长线于点 . 下列说法:①;②若 , , 则;③;④;⑤若 , , 则的面积为 , 正确的有 . (填序号)
三、解答题
-
14. 如图,在中, , , .求的值.
 15. 如图,在平面直角坐标系中,点在双曲线上,点B在双曲线上,且满足 , 连接 .
15. 如图,在平面直角坐标系中,点在双曲线上,点B在双曲线上,且满足 , 连接 .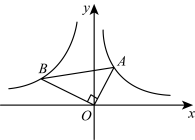 (1)、求双曲线的表达式;(2)、若 , 求的值.
(1)、求双曲线的表达式;(2)、若 , 求的值.四、综合题
-
16. 如图,是的直径,点是圆上的一点,于点 , 交于点 , 连接 , 若平分 , 过点作于点交于点 .
 (1)、求证:是的切线;
(1)、求证:是的切线;
(2)、延长和交于点 , 若 , 求的值;
(3)、在的条件下,求的值.17. 如图,已知二次函数的图像交轴于点 , , 交轴于点 . (1)、求这个二次函数的表达式;(2)、如图 , 点从点出发,以每秒个单位长度的速度沿线段向点运动,点从点出发,以每秒个单位长度的速度沿线段向点运动,点 , 同时出发.设运动时间为秒().当为何值时,的面积最大?最大面积是多少?(3)、已知是抛物线上一点,在直线上是否存在点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,直接写出点坐标;若不存在,请说明理由.
(1)、求这个二次函数的表达式;(2)、如图 , 点从点出发,以每秒个单位长度的速度沿线段向点运动,点从点出发,以每秒个单位长度的速度沿线段向点运动,点 , 同时出发.设运动时间为秒().当为何值时,的面积最大?最大面积是多少?(3)、已知是抛物线上一点,在直线上是否存在点 , 使以 , , , 为顶点的四边形是平行四边形?若存在,直接写出点坐标;若不存在,请说明理由.