2024年河北省初中毕业生升学文化课模拟考试数学试卷(五)(三年内高频考点)
试卷更新日期:2024-03-19 类型:中考模拟
一、选择题
-
1. 如图是小周同学在校运会上投掷实心球的场景,当投掷完毕时,测量员选取AB的长度作为小周的成绩,其依据是( ).
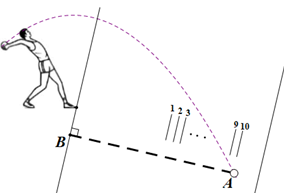 A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、过一点有且只有一条直线与已知直线垂直2. 教材中“整式的加减”一章的知识结构如图所示,则M和N分别代表的是( )
A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、过一点有且只有一条直线与已知直线垂直2. 教材中“整式的加减”一章的知识结构如图所示,则M和N分别代表的是( ) A、多项式,次数 B、单项式,合并同类项 C、系数,次数 D、多项式,合并同类项3. 若 , 则下列式子中,不正确的是( )A、 B、 C、 D、4. 已知 , , 则用表示为( )A、 B、 C、 D、5. 某同学在解方程时,把“( )”处的数看成了它的相反数,解得 , 则该方程的正确解应为( )A、 B、 C、 D、6. 如图是一正方体的表面展开图.将其折叠成正方体后,与顶点K距离最远的顶点是( )
A、多项式,次数 B、单项式,合并同类项 C、系数,次数 D、多项式,合并同类项3. 若 , 则下列式子中,不正确的是( )A、 B、 C、 D、4. 已知 , , 则用表示为( )A、 B、 C、 D、5. 某同学在解方程时,把“( )”处的数看成了它的相反数,解得 , 则该方程的正确解应为( )A、 B、 C、 D、6. 如图是一正方体的表面展开图.将其折叠成正方体后,与顶点K距离最远的顶点是( )
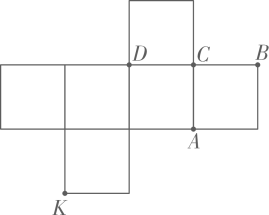 A、A点 B、B点 C、C点 D、D点7. 如图,在四边形中, , 以点为圆心,以任意长为半径作弧,分别交 , 于点 , , 分别以 , 为圆心,以大于长为半径作弧,两弧在内交于点 , 作射线 , 交于点 , 交的延长线于点若 , , 则的长为( )
A、A点 B、B点 C、C点 D、D点7. 如图,在四边形中, , 以点为圆心,以任意长为半径作弧,分别交 , 于点 , , 分别以 , 为圆心,以大于长为半径作弧,两弧在内交于点 , 作射线 , 交于点 , 交的延长线于点若 , , 则的长为( )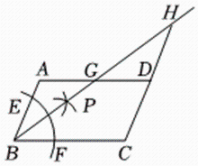 A、 B、 C、 D、8. 如图,在正方形ABCD中,AB=4,AC与 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交 于点N′,则PN-MN′的值为( )
A、 B、 C、 D、8. 如图,在正方形ABCD中,AB=4,AC与 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交 于点N′,则PN-MN′的值为( )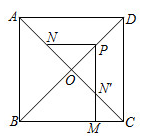 A、 B、 C、 D、9. 已知三角形的三边长分别为a,b,c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式 , 其中;我国南宋时期数学家秦九韶(约1202—1261)曾提出利用三角形的三边求其面积的秦九韶公式 , 若一个三角形的三边长分别为2,3,4,则其面积是( )A、 B、 C、 D、10. 剪纸艺术是我国的非物质文化遗产,如图是以正八边形为背景图形设计成的剪纸作品,记正八边形的面积为 , 图中阴影部分面积 , 则的值为( )
A、 B、 C、 D、9. 已知三角形的三边长分别为a,b,c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式 , 其中;我国南宋时期数学家秦九韶(约1202—1261)曾提出利用三角形的三边求其面积的秦九韶公式 , 若一个三角形的三边长分别为2,3,4,则其面积是( )A、 B、 C、 D、10. 剪纸艺术是我国的非物质文化遗产,如图是以正八边形为背景图形设计成的剪纸作品,记正八边形的面积为 , 图中阴影部分面积 , 则的值为( ) A、 B、 C、 D、11. 数轴上A,B,C三点所代表的数分别是a、b、2,且 .下列四个选项中,有( )个能表示A,B,C三点在数轴上的位置关系.
A、 B、 C、 D、11. 数轴上A,B,C三点所代表的数分别是a、b、2,且 .下列四个选项中,有( )个能表示A,B,C三点在数轴上的位置关系.①
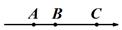 ②
② 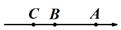 ③
③ 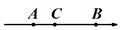 ④
④ 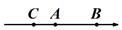 A、1个 B、2个 C、3个 D、4个12. 如图, 是 的八等分点. 若 , 四边形 的周长分别为 a, b,则下列判断正确的是( )
A、1个 B、2个 C、3个 D、4个12. 如图, 是 的八等分点. 若 , 四边形 的周长分别为 a, b,则下列判断正确的是( )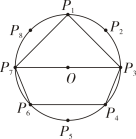 A、a<b B、a=b C、a>b D、a,b大小无法比较13. 已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:
A、a<b B、a=b C、a>b D、a,b大小无法比较13. 已知△ABC中,AB=AC,求证:∠B<90°,下面写出运用反证法证明这个命题的四个步骤:①∴∠A+∠B+∠C> 180°,这与三角形内角和为180°矛盾.
②因此假设不成立,∠B<90°.
③假设在△ABC中,∠B≥90°.
④由AB=AC,得∠B=∠C≥90° ,即∠B+∠C≥180°.
这四个步骤正确的顺序应是( )
A、④③①② B、③④②① C、①②③④ D、③④①②14. 汽车的“燃油效率”是指汽车每消耗 1L汽油最多可行驶的公里数,如图描述了A,B 两辆汽车在不同速度下的燃油效率情况.根据图中信息,下面4个推断中,合理的是 ( )①消耗 1L汽油,A车最多可行驶5km;
②B车以40km/h的速度行驶 1h,最少消耗 4L 汽油;
③对于A车而言,行驶速度越快越省油;
④某城市机动车最高限速80km/h,相同条件下,在该市驾驶 B车比驾驶A 车更省油.
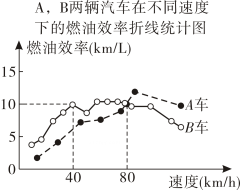 A、①④ B、②③ C、②④ D、①③④15. 若二次根式 有意义,且关于x的分式方程 +2= 有正数解,则符合条件的整数m的和是( )A、﹣7 B、﹣6 C、﹣5 D、﹣416. 如图,分别是半圆O的直径和弦, , , D是上的一个动点,连接AD.过点C作于E,连接 , 则的最小值是( )
A、①④ B、②③ C、②④ D、①③④15. 若二次根式 有意义,且关于x的分式方程 +2= 有正数解,则符合条件的整数m的和是( )A、﹣7 B、﹣6 C、﹣5 D、﹣416. 如图,分别是半圆O的直径和弦, , , D是上的一个动点,连接AD.过点C作于E,连接 , 则的最小值是( )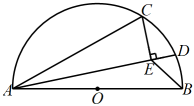 A、 B、 C、2 D、3
A、 B、 C、2 D、3二、填空题
-
17. 如图,小山的东侧炼A处有一个热气球,由于受西风的影响,以30(米/分)的速度沿与地面成75°角的方向飞行,20分后到达点C处,此时热气球上的人测得小山西侧点B处的俯角为30°,则小山东西两侧A,B两点间的距离为米(结果保留根号).
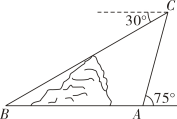 18. 如图所示,将一张长为 , 宽为的长方形纸片沿虚线剪成个直角三角形,拼成如图的正方形(相邻纸片之间不重叠,无缝隙),若正方形的面积为 , 中间空白处的正方形的面积为 , 则:
18. 如图所示,将一张长为 , 宽为的长方形纸片沿虚线剪成个直角三角形,拼成如图的正方形(相邻纸片之间不重叠,无缝隙),若正方形的面积为 , 中间空白处的正方形的面积为 , 则: (1)、m+n;(2)、原长方形纸片的周长是(用m表示).19. 如图,在中, , , , 的顶点在轴的正半轴上,点 , 点在第一象限,且直角边平行于轴,反比例函数且的图象经过点和边的中点 , 则的值为 .
(1)、m+n;(2)、原长方形纸片的周长是(用m表示).19. 如图,在中, , , , 的顶点在轴的正半轴上,点 , 点在第一象限,且直角边平行于轴,反比例函数且的图象经过点和边的中点 , 则的值为 .
三、解答题
-
20. 求证:当是整数时,两个连续奇数的平方差是这两个奇数的和的倍.21. 随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.(1)、求这两个月中该景区游客人数的月平均增长率;(2)、预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?22. 某水果公司新进了千克柑橘,销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在下表中:
柑橘总质量(/千克)
损坏柑橘质量(/千克)
柑橘损坏的频率()
(1)、写出 ▲ ▲ ▲ (精确到).(2)、估计这批柑橘的损坏概率为 ▲ (精确到).(3)、该水果公司以元每千克的成本进的这批柑橘,公司希望这批柑橘能够获得利润元,那么在出售柑橘(已去掉损坏的柑橘)时,求出每千克大约定价为多少元时比较合适(精确到).23. 已知与成正比例,且时, .(1)、求与的函数关系式;(2)、将所得函数图象向上平移个单位,求平移后直线与坐标轴围成的三角形的面积.24.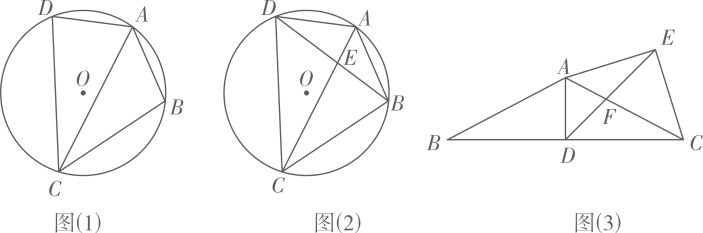 (1)、【感知】如图(1)已知四边形是圆O的内接四边形, , 易知 . (不用证明)(2)、【拓展】在【感知】的条件下,与交于点E,已知 , , 求的长.(3)、【应用】已知中 , 点D为中点,以为斜边向上作等腰直角三角形,当把的面积分为两部分时, .25. 在平面直角坐标系中,已知抛物线 .(1)、求该抛物线的对称轴(用含a的式子表示);(2)、若 , 当时,求y的取值范围;(3)、已知 , , 为该抛物线上的点,若 , 求a的取值范围.26. 如图1,在平面直角坐标系中,已知点 , , 且 , 满足 .
(1)、【感知】如图(1)已知四边形是圆O的内接四边形, , 易知 . (不用证明)(2)、【拓展】在【感知】的条件下,与交于点E,已知 , , 求的长.(3)、【应用】已知中 , 点D为中点,以为斜边向上作等腰直角三角形,当把的面积分为两部分时, .25. 在平面直角坐标系中,已知抛物线 .(1)、求该抛物线的对称轴(用含a的式子表示);(2)、若 , 当时,求y的取值范围;(3)、已知 , , 为该抛物线上的点,若 , 求a的取值范围.26. 如图1,在平面直角坐标系中,已知点 , , 且 , 满足 .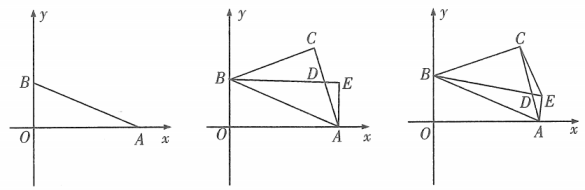
图1 图2 图3
(1)、求的面积;(2)、如图1,以为斜边构造等腰直角 , 请直接写出点的坐标;(3)、如图2,已知等腰直角中, , , 点是腰上的一点(不与 , 重合),连接 , 过点作 , 垂足为点 .①若是的角平分线,求证:;
②探究:如图3,连接 , 当点在线段上运动时(不与 , 重合),的大小是否发生变化?若改变,求出它的最大值;若不改变,求出这个定值.