人教版数学九年级下册 28.1 锐角三角函数同步分层训练 基础题
试卷更新日期:2024-03-19 类型:同步测试
一、选择题
-
1. 如图,在中, , 那么的值为( )
 A、 B、2 C、 D、2. 如图,已知⊙O的圆心在原点,半径OA=1,设∠AOP=a(a<90°),其始边OA与x轴重合,终边与⊙О相交于点P,设点P的坐标为(x,y),⊙O的切线AT交OP于点T,且AT=m,则下列结论中,错误的是( )
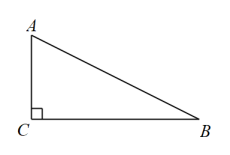
A、 B、2 C、 D、2. 如图,已知⊙O的圆心在原点,半径OA=1,设∠AOP=a(a<90°),其始边OA与x轴重合,终边与⊙О相交于点P,设点P的坐标为(x,y),⊙O的切线AT交OP于点T,且AT=m,则下列结论中,错误的是( ) A、 B、 C、 D、与成反比例3. 如图,已知Rt△ABC中,∠C=90°,AC=8,BC=15,则tanA的值为( )
A、 B、 C、 D、与成反比例3. 如图,已知Rt△ABC中,∠C=90°,AC=8,BC=15,则tanA的值为( ) A、 B、 C、 D、4. 如图,在中, , 于点 , 则下列结论不正确的是( )
A、 B、 C、 D、4. 如图,在中, , 于点 , 则下列结论不正确的是( ) A、 B、 C、 D、5. 在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A、 B、 C、 D、5. 在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A、不变 B、扩大5倍 C、缩小5倍 D、不能确定6. 如图,建筑物CD和旗杆AB的水平距离BD为9m,在建筑物的顶端C测得旗杆顶部A的仰角为30°,旗杆底部B的俯角为45°,则旗杆AB的高度为( ) A、 B、 C、 D、7. 西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中,立柱AC高为a.已知,冬至时北京的正午日光入射角∠ABC约为26.5°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( )
A、 B、 C、 D、7. 西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中,立柱AC高为a.已知,冬至时北京的正午日光入射角∠ABC约为26.5°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( ) A、 B、asin26.5° C、acos26.5° D、8. 在中, , 下列三角函数正确的是( )A、 B、 C、 D、
A、 B、asin26.5° C、acos26.5° D、8. 在中, , 下列三角函数正确的是( )A、 B、 C、 D、二、填空题
-
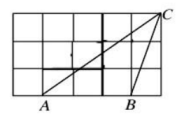
9. 计算:.10. 如图,△ABC的顶点都在方格纸的格点上,则cosA=
 11. 如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中虚线剪掉,用剩下的纸板折成一个底面为正三角形的无盖柱形盒子,则它的容积为cm³.
11. 如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中虚线剪掉,用剩下的纸板折成一个底面为正三角形的无盖柱形盒子,则它的容积为cm³. 12. 小明同学测量一个圆形零件的半径时,他将直尺、三角板和这个零件如图放置于桌面上,零件与直尺,三角板均相切,测得点A与其中一个切点B的距离为3cm,则这个零件的半径是cm.
12. 小明同学测量一个圆形零件的半径时,他将直尺、三角板和这个零件如图放置于桌面上,零件与直尺,三角板均相切,测得点A与其中一个切点B的距离为3cm,则这个零件的半径是cm.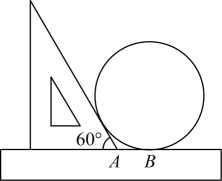 13. 如图,在△ABC中,CA=CB=4,∠BAC=α,将△ABC绕点A逆时针旋转2α,得到△AB'C',连结B'C并延长交AB于点D,当B'D⊥AB时,的长是.
13. 如图,在△ABC中,CA=CB=4,∠BAC=α,将△ABC绕点A逆时针旋转2α,得到△AB'C',连结B'C并延长交AB于点D,当B'D⊥AB时,的长是.
三、解答题
-
14. 如图,在矩形ABCD中,AC为对角线, , 垂足为点E.
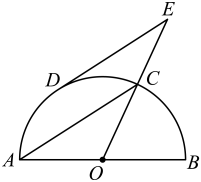
 (1)、求证:;(2)、若 , , 求的长.15. 如图,AB是的直径,AC , BC是弦,点D在AB的延长线上,且 , 的切线AE与DC的延长线交于点E.
(1)、求证:;(2)、若 , , 求的长.15. 如图,AB是的直径,AC , BC是弦,点D在AB的延长线上,且 , 的切线AE与DC的延长线交于点E. (1)、求证:CD是的切线;(2)、若的半径为2, , 求AE的长.
(1)、求证:CD是的切线;(2)、若的半径为2, , 求AE的长.四、综合题