2024年四川省成都市中考数学模拟卷(一)
试卷更新日期:2024-03-19 类型:中考模拟
一、选择题
-
1. 2024的相反数是A、 B、 C、2024 D、-20242. 温家宝总理有句名言:多么小的问题乘以13亿,都会变得很大;多么大的经济总量,除以13亿都会变得很小.将13亿用科学记数法表示为( )A、
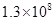 B、
B、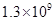 C、
C、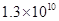 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )时间/小时
7
8
9
10
人数
7
9
11
3
A、9,8 B、9,8.5 C、10,9 D、11,8.55. 如图,菱形中,连接 , 若 , 则的度数为( )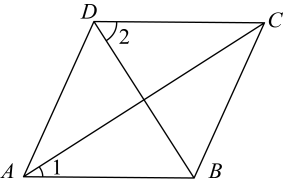 A、 B、 C、 D、6. 如图,和△是以点为位似中心的位似三角形,若为的中点, , 则的面积为
A、 B、 C、 D、6. 如图,和△是以点为位似中心的位似三角形,若为的中点, , 则的面积为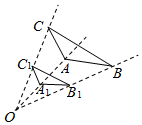 A、15 B、12 C、9 D、67. 某种柑橘果肉清香、酸甜适度,深受人们的喜爱,也是馈赠亲友的上佳礼品.首批柑橘成熟后,某电商用3500元购进这种柑橘进行销售,面市后,线上订单猛增,供不应求,该电商又用2500元购进第二批这种柑橘,由于更多柑橘成熟,单价比第一批每箱便宜了4元,但数量与第一批的数量一样多,求购进的第一批柑橘的单价.设购进的第一批柑橘的单价为x元,根据题意可列方程为( )A、 B、 C、 D、8. 已知二次函数y=a2-bx+c(a≠0)的图象如图,有下列5个结论:①abc<o;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.其中正确的结论有( )
A、15 B、12 C、9 D、67. 某种柑橘果肉清香、酸甜适度,深受人们的喜爱,也是馈赠亲友的上佳礼品.首批柑橘成熟后,某电商用3500元购进这种柑橘进行销售,面市后,线上订单猛增,供不应求,该电商又用2500元购进第二批这种柑橘,由于更多柑橘成熟,单价比第一批每箱便宜了4元,但数量与第一批的数量一样多,求购进的第一批柑橘的单价.设购进的第一批柑橘的单价为x元,根据题意可列方程为( )A、 B、 C、 D、8. 已知二次函数y=a2-bx+c(a≠0)的图象如图,有下列5个结论:①abc<o;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.其中正确的结论有( )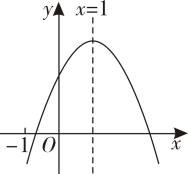 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
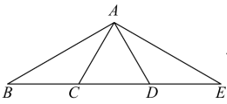
9. 分解因式: .10. 若点 , 都在一次函数的图象上,则 . (填“”或“”)11. 如图,点B , E是等边三角形的边所在直线上的两点,且 , 则度.
 12. 已知点A(a ,b)关于x轴对称点的坐标是(a , -12),关于y轴对称点的坐标 是(5,b),则A点的坐标是.13. 如图,在ΔABC中,∠C=90°,∠B=22.5°,AC=2,分别以点A,B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接 , 则BD的长为.
12. 已知点A(a ,b)关于x轴对称点的坐标是(a , -12),关于y轴对称点的坐标 是(5,b),则A点的坐标是.13. 如图,在ΔABC中,∠C=90°,∠B=22.5°,AC=2,分别以点A,B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接 , 则BD的长为.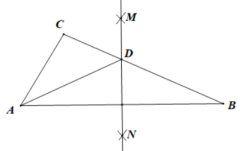
三、解答题
-
14.(1)、计算:;(2)、解方程:.15. 学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校.某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为三类:A:好,B:中,:差.请根据图中信息,解答下列问题:
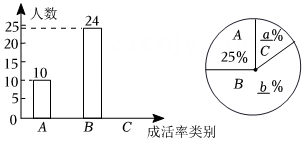 (1)、求全班学生总人数;(2)、在扇形统计图中, , , 类的圆心角为;(3)、张老师在班上随机抽取了4名学生,其中类1人,类2人,类1人,若再从这4人中随机抽取2人,请用列表法或画树状图的方法求出全是类学生的概率.16. 教育部布的《基础教育课程改革纲要》要求每位学生每学年都要参加社会实践活动,某学校组织了一次测量探究活动,如图,某大楼的顶部竖有一块广告牌CD , 小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度1: ,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据: ≈1.41, ≈1.73,tan53°≈ ,cos53°≈0.60)
(1)、求全班学生总人数;(2)、在扇形统计图中, , , 类的圆心角为;(3)、张老师在班上随机抽取了4名学生,其中类1人,类2人,类1人,若再从这4人中随机抽取2人,请用列表法或画树状图的方法求出全是类学生的概率.16. 教育部布的《基础教育课程改革纲要》要求每位学生每学年都要参加社会实践活动,某学校组织了一次测量探究活动,如图,某大楼的顶部竖有一块广告牌CD , 小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度1: ,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据: ≈1.41, ≈1.73,tan53°≈ ,cos53°≈0.60) 17. 如图,是的直径,点C为外一点,过点 C作于点D,交于点F,连接 , 与相交于点A,点P为线段上一点,且
17. 如图,是的直径,点C为外一点,过点 C作于点D,交于点F,连接 , 与相交于点A,点P为线段上一点,且 (1)、求证:为的切线;(2)、若点F为的中点,的半径为5, , 求的长.18. 直线与轴交于点 , 与轴交于点 , 并与双曲线交于点 , 连接OA.
(1)、求证:为的切线;(2)、若点F为的中点,的半径为5, , 求的长.18. 直线与轴交于点 , 与轴交于点 , 并与双曲线交于点 , 连接OA.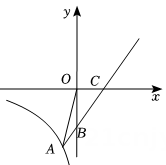 (1)、求直线与双曲线的解析式.(2)、在直线AC上存在一个点(不与重合),使得 , 求点的坐标.(3)、若点在轴的正半轴上,是否存在以点D、C、B构成的三角形与相似?若存在求出点的坐标,若不存在,请说明理由.
(1)、求直线与双曲线的解析式.(2)、在直线AC上存在一个点(不与重合),使得 , 求点的坐标.(3)、若点在轴的正半轴上,是否存在以点D、C、B构成的三角形与相似?若存在求出点的坐标,若不存在,请说明理由.四、B卷填空题
-
19. 关于x的方程 有两个实数根 .且 .则 .20. 当 时,代数式 的值是 .21. 如图,正方形的对角线交于点中, , 将绕点旋转(边在正方形外面),现随机向正方形内抛掷一枚小针,则针尖落在与正方形重叠部分的概率为 .
 22. 如图,四边形为矩形,点在第三象限,点关于的对称点为点 , 点 , 都在函数的图象上,轴于点.若的延长线交轴于点 , 当矩形的面积为6时,的值为.
22. 如图,四边形为矩形,点在第三象限,点关于的对称点为点 , 点 , 都在函数的图象上,轴于点.若的延长线交轴于点 , 当矩形的面积为6时,的值为. 23. 如图,在中, , E为边上一点,以为直径的半圆O与相切于点D,连接 , . P是边上的动点,当为等腰三角形时,的长为 .
23. 如图,在中, , E为边上一点,以为直径的半圆O与相切于点D,连接 , . P是边上的动点,当为等腰三角形时,的长为 .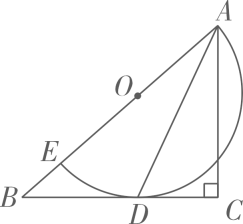
五、B卷解答题
-
24. 某造纸厂生产甲、乙两种生活用纸的相关信息如下表,其中x(吨)表示甲、乙两种生活用纸的月产量,请根据表中的信息解答后面的问题:
种
品
价
目
出厂价(元/吨)
成本价(元/吨)
排污处理费
甲种生活用纸
4800
2200
200(元/吨)
每月还需支付设备管理、
维护费20000元
乙种生活用纸
7000﹣10x
1600
400(元/吨)
(1)设该造纸厂每月生产甲、乙两种生活用纸的利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入﹣总支出);
(2)若某月要生产甲、乙两种生活用纸共300吨,求该月生产甲、乙两种生活用纸各多少吨,获得的总利润最大?最大利润是多少?
25. 如图,在平面直角坐标系中,点O为坐标系的原点,抛物线y=-x2+bx+c与x轴相交于点A和点B , 与y轴相交于点C , 直线y=-x+3经过点B和点C .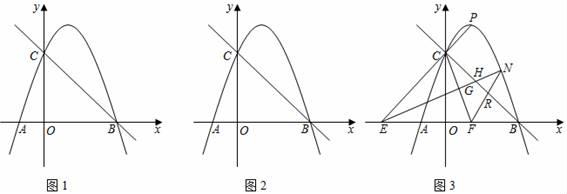 (1)、求抛物线的解析式;(2)、点P为第一象限内抛物线上一点,过点P作y轴的平行线交线段BC于点D , 设PD=d , 点P的横坐标为t , 求d与t之间的函数关系式;(3)、在(2)的条件下,点P为抛物线的顶点,连接PC并延长交x轴于点E , 点F为线段OB上的点,连接CF , 过点E作EG⊥CF于点G , 射线EG交线段BC于点H , 交抛物线于点N , 连接FN交线段BC于点R , 若∠CFN=2∠NEA , 求点N的坐标.26.
(1)、求抛物线的解析式;(2)、点P为第一象限内抛物线上一点,过点P作y轴的平行线交线段BC于点D , 设PD=d , 点P的横坐标为t , 求d与t之间的函数关系式;(3)、在(2)的条件下,点P为抛物线的顶点,连接PC并延长交x轴于点E , 点F为线段OB上的点,连接CF , 过点E作EG⊥CF于点G , 射线EG交线段BC于点H , 交抛物线于点N , 连接FN交线段BC于点R , 若∠CFN=2∠NEA , 求点N的坐标.26. (1)、【观察与猜想】
(1)、【观察与猜想】如图1,点是矩形内一点,过点的直线 , 分别交矩形的边为点 . 若 , 则;
(2)、【类比探究】如图2,在平行四边形中,点分别在边上,连接与交于点 . 求证:;
(3)、【拓展延伸】如图3,在四边形中, , 在边上,连接与交于点 , 当时,求的值.