2023-2024学年人教版初中数学七年级下册 8.3 实际问题与二元一次方程组 同步分层训练 培优题
试卷更新日期:2024-03-19 类型:同步测试
一、选择题
-
1. 装乒乓球的盒子有两种,大盒装6个,小盒装4个,若将50个乒乓球都装进盒子且把每个盒子都装满,那么不同的装球方法有( )A、3种 B、4种 C、5种 D、6种2. 一道来自课本的习题:
从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙,地全程是多少?小红将这个实际问题转化为二元一次方程组题,设未知数x, y,已列出一个方程 , 则另一个方程正确的是( )
A、 B、 C、 D、3. 中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有个,甜果有个,则可列方程组为( )A、 B、 C、 D、4. 为喜迎“全国两会”胜利召开,某校开展了以“永远跟党走,奋进新征程”为主题的演讲活动,现计划拿出200元钱全部用于购买甲、乙两种奖品(两种奖品都购买),奖励表现突出的同学,已知甲种奖品每件15元,乙种奖品每件10元,则购买方案有( )A、6种 B、5种 C、4种 D、3种5. 如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则小长方形的周长为( ) A、20 B、22 C、24 D、266. 如果方程组与有相同的解,则的值是( )A、2023 B、1 C、0 D、7. 小聪去商店买笔记本和钢笔,共用了60元钱,已知每本笔记本2元,每支钢笔5元,若笔记本和钢笔都购买,且笔记本的数量多于钢笔的数量,则小聪的购买方案有( )A、3种 B、4种 C、5种 D、6种8. 如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍,如果搭建的正三角形和正六边形共用了2023根火柴,并且正三角形的个数比正六边形的个数多 个,那么能连续搭建的正三角形的个数是( )
A、20 B、22 C、24 D、266. 如果方程组与有相同的解,则的值是( )A、2023 B、1 C、0 D、7. 小聪去商店买笔记本和钢笔,共用了60元钱,已知每本笔记本2元,每支钢笔5元,若笔记本和钢笔都购买,且笔记本的数量多于钢笔的数量,则小聪的购买方案有( )A、3种 B、4种 C、5种 D、6种8. 如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍,如果搭建的正三角形和正六边形共用了2023根火柴,并且正三角形的个数比正六边形的个数多 个,那么能连续搭建的正三角形的个数是( )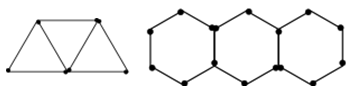 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
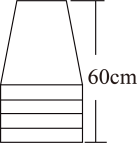
9. 某公园的门票价格为:成人票8元/张,儿童票3元/张,某旅游团买门票共花费44元,则该旅游团去公园游玩的人数是 .10. 塑料凳子轻便实用,在生活中随处可见.如图,若4个塑料凳子叠放在一起的高度为60cm,6个塑料凳子叠放在一起的高度为70cm.当有11个塑料凳子整齐的叠放在一起时,其高度是cm.
 11. 如图,把一个大长方形分割成小块,其中长方形号和号,号和号的形状和大小分别相同,号是正方形,则号的面积与大长方形的面积之比为 .
11. 如图,把一个大长方形分割成小块,其中长方形号和号,号和号的形状和大小分别相同,号是正方形,则号的面积与大长方形的面积之比为 . 12. 甲、乙两班为运动会订购一批啦啦球,甲班开始订购的啦啦球数量是乙班订购数量的3倍,后来由于某种原因,甲班决定把自己所订购的啦啦球数量转让7个给乙班,但由于商家失误,寄来的啦啦球总数比甲、乙两班所定购的总数少了七个,最后甲班所购啦啦球数量是乙班所购数量的2倍,那么甲、乙两班最后所得的啦啦球总数最多是13. 江津花椒以“鲜香麻”闻名,深受重庆人民的喜爱. 其中甲品种最麻, 乙品种次之,丙 品种最后.去年,江津某县种植的甲、乙、丙三种品种的面积之比为 2:3: 5.今年 因需求量的增加,该县决定将其种植面积扩大.计划将扩大部分的 用于种植丙品种,则丙品种的种植面积将达到这三种花椒种植总面积的 ;扩大部分的剩余面积全部用 于种植甲品种和乙品种,为了使甲品种的种植面积与乙品种的种植面积之比达到 , 则该县种扩大种植甲品种的面积与该县种植这三种花椒的总面积之比是 .
12. 甲、乙两班为运动会订购一批啦啦球,甲班开始订购的啦啦球数量是乙班订购数量的3倍,后来由于某种原因,甲班决定把自己所订购的啦啦球数量转让7个给乙班,但由于商家失误,寄来的啦啦球总数比甲、乙两班所定购的总数少了七个,最后甲班所购啦啦球数量是乙班所购数量的2倍,那么甲、乙两班最后所得的啦啦球总数最多是13. 江津花椒以“鲜香麻”闻名,深受重庆人民的喜爱. 其中甲品种最麻, 乙品种次之,丙 品种最后.去年,江津某县种植的甲、乙、丙三种品种的面积之比为 2:3: 5.今年 因需求量的增加,该县决定将其种植面积扩大.计划将扩大部分的 用于种植丙品种,则丙品种的种植面积将达到这三种花椒种植总面积的 ;扩大部分的剩余面积全部用 于种植甲品种和乙品种,为了使甲品种的种植面积与乙品种的种植面积之比达到 , 则该县种扩大种植甲品种的面积与该县种植这三种花椒的总面积之比是 .三、解答题
-
14. 甲、乙两人共同解方程组 .解题时由于甲看错了方程①中的a,得到方程组的解为 ;乙看错了方程②中的b,得到方程组的 ,试计算a2019+( b)2020的值.15. 某企业在“蜀南竹海”收购毛竹,直接销售,每吨可获利100元,进行粗加工,每天可加工8吨,每吨可获利800元;如果对毛竹进行精加工,每天可加工1吨,每吨可获利4000元.由于受条件限制,每天只能采用一种方式加工,要求将在一月内(30天)将这批毛竹93吨全部销售.为此企业厂长召集职工开会,让职工讨论如何加工销售更合算.
甲说:将毛竹全部进行粗加工后销售;
乙说:30天都进行精加工,未加工的毛竹直接销售;
丙说:30天中可用几天粗加工,再用几天精加工后销售;
请问厂长应采用哪位说的方案做,获利最大?
四、综合题