2023-2024学年人教版初中数学七年级下册 8.3 实际问题与二元一次方程组同步分层训练提升题

试卷更新日期：2024-03-19 类型：同步测试

进入出卷网下载

一、选择题

1. 篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分某队在10场比赛中得到17分，设这个队胜x场，负y场，则x，y的值为（）

A、 ${\begin{array}{l} x = 8 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 7 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x = 6 \\ y = 4 \end{array}$ D、 ${\begin{array}{l} x = 5 \\ y = 5 \end{array}$

查看试题解析
2. 为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神，湘潭市举办了第10届青少年机器人竞赛.组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共12个，若桌子腿数与凳子腿数的和为40条，则每个比赛场地有几张桌子和几条凳子？设有x张桌子，有y条凳子，根据题意所列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 40 \\ 4 x + 3 y = 12 \end{array}$ B、 ${\begin{array}{l} x + y = 12 \\ 4 x + 3 y = 40 \end{array}$ C、 ${\begin{array}{l} x + y = 40 \\ 3 x + 4 y = 12 \end{array}$ D、 ${\begin{array}{l} x + y = 12 \\ 3 x + 4 y = 40 \end{array}$

查看试题解析
3. 端午节前夕，某食品加工厂准备将生产的粽子装入A，B两种食品盒中，A种食品盒每盒装8个粽子，B种食品盒每盒装10个粽子.若要将200个粽子分别装入A，B两种食品盒中(两种食品盒均要使用并且装满)，则不同的分装方式有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
4. 如图，第一个天平的两侧分别放2个球体和5个圆柱体，第二个天平的两侧分别放2个正方体和3个圆柱体，两个天平都平衡，则6个球体的质量等于（）个正方体的质量.

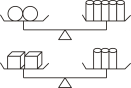A、4 B、6 C、8 D、10

查看试题解析
5. 把一根长 $15 m$ 的钢管截成 $2 m$ 和 $3 m$ 长两种规格的钢管，要求材料全部用完且每种都必须有，则不同的截法有（）

A、4种 B、3种 C、2种 D、1种

查看试题解析

6. 一道来自课本的习题：

从甲地到乙地有一段上坡与一段平路，如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54min，从乙地到甲地需42min，甲地到乙地全程是多少？

小红将这个实际问题转化为二元一次方程组问题，设未知数x，y，已经列出一个方程 $\frac{x}{3} + \frac{y}{4} = \frac{54}{60}$ ，则另一个方程正确的是（）

A、

\frac{x}{4} + \frac{y}{3} = \frac{42}{60}

B、

\frac{x}{5} + \frac{y}{4} = \frac{42}{60}

C、

\frac{x}{4} + \frac{y}{5} = \frac{42}{60}

D、

\frac{x}{3} + \frac{y}{4} = \frac{42}{60}

查看试题解析

7. 某市举行中学生足球比赛，每队胜一场得3分，负一场得1分，本次足球比赛没有平局，下表是市实验学校比赛信息（不完整），则该校获胜的场数为（）

	胜	负	合计
场数		y	12
积分	$3 x$		28

A、6场 B、7场 C、8场 D、9场

查看试题解析

8. 若关于x、y的方程组 ${\begin{array}{l} x + y = 2 \\ a x + 2 y = 8 \end{array}$ 的解为整数，则满足条件的所有整数a的值的和为（）

A、6 B、9 C、12 D、16

查看试题解析

二、填空题

9. 现有1元的人民币 $x$ 张，5元的人民币 $y$ 张，共120元，这个关系用方程可以表示为.

查看试题解析
10. 某人只带了2元和5元两种货币，他要买一件27元的商品，而商店不给找钱，则此人的付款方式有种．

查看试题解析
11. 已知关于x ， y的方程组 ${\begin{cases} 2 x + y = 2 a + 1 \\ x + 2 y = a - 1 \end{cases}$ 的解满足x－y＝6，则a的值为．

查看试题解析

12. 一道来自课本的习题：

从甲地到乙地有一段上坡与一段平路．如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54min，从乙地到甲地需42min．甲地到乙地全程是多少？

小红将这个实际问题转化为二元一次方程组问题，设未知数x ， y ，已经列出一个方程 $\frac{x}{3} + \frac{y}{4} = \frac{54}{60}$ ，则另一个方程是．

查看试题解析

13. 某贸易公司有120吨商品需要运出，现有甲、乙、丙三种车型供运输选择．每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
车型
甲
乙
丙
运载量（吨/辆）
5
8
10
运费（元/辆）
450
600
700

(1)、全部商品一次性运送可用甲型车8辆．乙型车5辆，丙型车辆．

(2)、若该公司打算用甲、乙、丙三种车型同时参与运送，已知车辆总数为14辆，且一次性运完所有商品，此时的总运费为元．

查看试题解析

三、解答题

14. 某车间10月份计划加工甲、乙两种零件共200个，由于采用新技术，实际产量为216个，其中甲零件超产10%，乙零件超产5%.求该车间10月份计划加工甲、乙零件各多少个？

查看试题解析
15. 已知关于x ， y的方程组 ${\begin{cases} m x + 2 n y = 4 \\ x + y = 2 \end{cases}$ 与 ${\begin{cases} x - y = 4 \\ n x + (m - 1) y = 3 \end{cases}$ 有相同的解．

(1)、求这个相同的解；

(2)、求m ， n的值；

(3)、若（1）中的解也是关于x ， y的方程 $(3 - a) x + (2 a + 1) y = 3$ 的解，求a的值．

查看试题解析

四、综合题

16. 五一节前，某商店拟用2000元的总价购进 $A$ 、 $B$ 两种品牌的电风扇进行销售，为更好的销售，每种品牌电风扇都至少购进1台，已知购进3台 $A$ 种品牌电风扇所需费用与购进2台 $B$ 种品牌电风扇所需费用相同，购进1台 $A$ 种品牌电风扇与2台 $B$ 种品牌电风共需费用800元

(1)、求 $A$ 、 $B$ 两种品牌电风扇每台的进价分别是多少元？

(2)、该商店将 $A$ 种品牌电风扇定价为280元/台， $B$ 种品牌电风扇定价为350元/台，为能在销售完这两种电风扇后获得最大的利润，该商店应采用哪种进货方案？

查看试题解析
17. 去年疫情期间某物流公司计划用两种车型运输救灾物资，已知：用 $2$ 辆 $A$ 型车和 $1$ 辆 $B$ 型车装满物资一次可运 $12$ 吨；用 $1$ 辆 $A$ 型车和 $2$ 辆 $B$ 型车一次可运 $15$ 吨．某物流公司现有 $21$ 吨货物资，计划同时租用 $A$ 型车 $a$ 辆， $B$ 型车 $b$ 辆，一次运完，且恰好每辆车都装满．

(1)、1辆 $A$ 型车和 $1$ 辆 $B$ 型车都装满物资一次可分别运多少吨？

(2)、请你帮该物流公司设计租车方案；

(3)、若 $A$ 型车每辆需租金每次 $100$ 元， $B$ 型车租金每次 $120$ 元，请选出最省钱的租车方案，并求出最少租车费．

查看试题解析

车型	甲	乙	丙
运载量（吨/辆）	5	8	10
运费（元/辆）	450	600	700

2023-2024学年人教版初中数学七年级下册 8.3 实际问题与二元一次方程组 同步分层训练 提升题

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年人教版初中数学七年级下册 8.3 实际问题与二元一次方程组同步分层训练提升题