2023-2024学年人教版初中数学七年级下册 8.2 消元----解二元一次方程组同步分层训练培优题

试卷更新日期：2024-03-19 类型：同步测试

进入出卷网下载

一、选择题

1. 方程组 ${\begin{array}{l} 5 x + 2 y = 25 \\ 3 x + 4 y = 15 \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 1 \\ y = 0 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ D、 ${\begin{array}{l} x = 5 \\ y = 0 \end{array}$

查看试题解析
2. 关于x，y的方程组 $\{\begin{matrix} y + 2 x = m \\ x + 2 y = 5 m \end{matrix}$ 的解满足x+y=6，则m的值为（　　）

A、1 B、2 C、3 D、4

查看试题解析
3. 已知 ${\begin{array}{l} x = 4 \\ y = 2 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 5 \\ b x + a y = 1 \end{array}$ 的解，则 $a - b$ 的值是（）

A、 $- 1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
4. 若 ${\begin{array}{l} x + 2 y = 2 \\ 2 x - k y = 6 \end{array}$ 解得 $x$ ， $y$ 的值互为相反数，则 $k$ 的值为（）

A、 $2$ B、 $- 1$ C、-5 D、4

查看试题解析
5. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是二元一次方程组 ${\begin{array}{l} m x + n y = 8 \\ n x - m y = 1 \end{array}$ 的解，则 $4 n - 2 m$ 的算术平方根是（）

A、2 B、 $\sqrt{2}$ C、±2 D、 $\pm \sqrt{2}$

查看试题解析
6. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x - 2 y = 2 k \\ 2 x + y = k + 1 \end{array}$ ，以下结论： $①$ 当 $k = 2$ 时，方程组的解也是方程 $3 x + y = 5$ 的解； $②$ 存在实数 $k$ ，使得 $x + y = 0$ ； $③$ 不论 $k$ 取什么实数， $3 x + 4 y$ 的值始终不变； $④$ 若 $2 x + 3 y = 3$ ，则 $k = 8 .$ 其中正确的是（）

A、①②③ B、①②④ C、①③④ D、①④

查看试题解析
7. 我们规定： $[m]$ 表示不超过 $m$ 的最大整数，例如： $[3.1] = 3$ ， $[0] = 0$ ， $[- 3.1] = - 4$ ，则关于 $x$ 和 $y$ 的二元一次方程组 ${\begin{array}{l} [x] + y = 3.2 \\ x - [y] = [3.2] \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 3 \\ y = 0.2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1.2 \end{array}$ C、 ${\begin{array}{l} x = 3.3 \\ y = 0.2 \end{array}$ D、 ${\begin{array}{l} x = 3.4 \\ y = 0.2 \end{array}$

查看试题解析
8. 甲、乙两人共同解关于x，y的方程组 ${\begin{matrix} a x + b y = 5 ① \\ 3 x + c y = 2 ② \end{matrix}$ ，甲符合题意地解得 ${\begin{matrix} x = 2 \\ y = - 1 \end{matrix}$ 乙看错了方程②中的系数c，解得 ${\begin{matrix} x = 3 \\ y = 1 \end{matrix}$ ，则 ${(a + b + c)}^{2}$ 的值为（）

A、16 B、25 C、36 D、49

查看试题解析

二、填空题

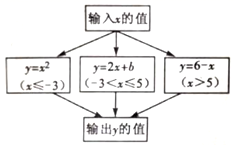
9. 已知|x+y|+|x|=x，且|4x+y-9|=0，则5x-y的值为

查看试题解析
10. 若x²^a-3b+2y^5a+b-10=0是二元一次方程，那么a、b的值分别是.

查看试题解析
11. 已知关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} a x + b y = 5 \\ b x + a y = 6 \end{array}$ 的解为 ${\begin{array}{l} x = 4 \\ y = 6 \end{array}$ 那么关于 $m$ 、 $n$ 的二元一次方程组 ${\begin{array}{l} a (m + n) + b (m - n) = 5 \\ b (m + n) + a (m - n) = 6 \end{array}$ 的解为．

查看试题解析
12. 已知关于 $x, y$ 的二元一次方程组 ${\begin{array}{l} a x + b y = 7 \\ b x + a y = 8 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ ，若 $m, n$ 满足二元一次方程组 ${\begin{array}{l} a (m + n) + b (m - n) = 7 \\ b (m + n) + a (m - n) = 8 \end{array}$ ，则 $m^{2} - n^{2} =$ ．

查看试题解析
13. 根据如图所示的程序计算函数y的值，若输入的x值是4或7时，输出的y值相等，则b等于

查看试题解析

三、解答题

14. 已知方程 $a x + b = 11$ ，小王正确解得x=3．小李由于粗心，把b看作6，解得x=5．试求a、b的值．

查看试题解析
15. 解关于x、y的方程组 ${\begin{matrix} a x + b y = 9 \\ 3 x - c y = - 2 \end{matrix}$ 时，甲符合题意地解得方程组的解为 ${\begin{matrix} x = 2 \\ y = 4 \end{matrix}$ ，乙因为把c抄错了，在计算无误的情况下解得方程组的解为 ${\begin{matrix} x = 4 \\ y = - 1 \end{matrix}$ ，求a、b、c的值．

查看试题解析

四、综合题

16. 已知关于x，y的方程组 ${\begin{array}{l} x + 2 y = 5 ， \\ x - 2 y + m x + 9 = 0. \end{array}$

(1)、若方程组的解满足 $x + y = 0$ ，求 $m$ 的值；

(2)、无论 $m$ 取何实数，方程 $x - 2 y + m x + 9 = 0$ 总有一个公共解，求出这个方程的公共解.

查看试题解析
17. 汛期即将来临，防汛指挥部在某水域一危险地带两岸各安置了一探照灯，便于夜间查看河水及两岸河堤的情况．如图1，灯 $A$ 射出的光束自 $A M$ 顺时针旋转至 $A N$ 便立即回转，灯 $B$ 射出的光束自 $B P$ 顺时针旋转至 $B Q$ 便立即回转，两灯不停交叉照射巡视．若灯 $A$ 射出的光束转动的速度是 $a °$ /秒，灯 $B$ 射出的光束转动的速度是 $b °$ /秒，且 $a$ 、 $b$ 满足 $| a - 3 b | + (a + b - 4)^{2} = 0$ ．假定这一带水域两岸河堤是平行的，即 $P Q / / M N$ ，且 $∠ B A N = 45 °$ ．

(1)、求 $a$ 、 $b$ 的值；

(2)、如图2，两灯同时转动，在灯 $A$ 射出的光束到达 $A N$ 之前，若两灯射出的光束交于点 $C$ ，过 $C$ 作 $C D ⊥ A C$ 交 $P Q$ 于点 $D$ ，若 $∠ B C D = 20 °$ ，求 $∠ B A C$ 的度数；

(3)、若灯 $B$ 射线先转动30秒，灯 $A$ 射出的光束才开始转动，在灯 $B$ 射出的光束到达 $B Q$ 之前， $A$ 灯转动几秒，两灯的光束互相平行?

查看试题解析

2023-2024学年人教版初中数学七年级下册 8.2 消元----解二元一次方程组 同步分层训练 培优题

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年人教版初中数学七年级下册 8.2 消元----解二元一次方程组同步分层训练培优题