2023-2024学年人教版初中数学七年级下册 7.2.2 用坐标表示平移同步分层训练培优题

试卷更新日期：2024-03-19 类型：同步测试

进入出卷网下载

一、选择题

1. 在平面直角坐标系中，将点 $A (x ， y)$ 先向左平移3个単位，再向上平移5个单位后与点 $B (- 3 ， 2)$ 重合，则点 $A$ 的坐标是（）

A、 $(2 ， 5)$ B、 $(0 ， - 3)$ C、 $(- 2 ， 5)$ D、 $(5 ， - 3)$

查看试题解析
2. 在平面直角坐标系中，点A(x，y)，B(3，4)，AB＝5，且AB∥x轴，则A点坐标为（）

A、(﹣3，4) B、(8，4) C、(3，9)或(﹣2，4) D、(﹣2，4)或(8，4)

查看试题解析
3. 在平面直角坐标系中，将 $A (1 ， m^{2})$ ，沿着 $y$ 轴的负方向向下平移 $2 m^{2} + 3$ 个单位后得到 $B$ 点．有四个点 $M (1 ， - m^{2} - 4)$ ， $N (1 ， - 2 m^{2} - 3)$ ， $P (1 ， - m^{2})$ ， $Q (1 ， - 3 m^{2})$ 一定在线段 $A B$ 上的是（）

A、点 $M$ B、点 $N$ C、点 $P$ D、点 $O$

查看试题解析
4. 如图，已知点 $A (1 ， 0)$ ， $B (4 ， m)$ ，若将线段 $A B$ 平移至 $C D$ ，其中点 $C (- 2 ， 1)$ ， $D (a ， n)$ ，则 $m - n$ 的值为（）

A、 $- 3$ B、 $- 1$ C、 $1$ D、 $3$

查看试题解析
5. 如图，在平面直角坐标系中，点A ， B ， P的坐标分别为 $(3 ， 0)$ ， $(0 ， 2)$ ， $(1 ， 4)$ ．若 $A B ∥ P Q$ ，且 $A B = P Q$ ，则点Q的坐标是（）

A、 $(－ 2 ， 6)$ 或 $(4 ， 2)$ B、 $(－ 2 ， 6)$ 或 $(5 ， 1)$ C、 $(4 ， 2)$ D、 $(5 ， 1)$

查看试题解析
6. 在平面直角坐标系中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P伴随点．已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …，这样依次得到点A₁ ， A₂ ， A₃ ， …，A_n ， …若点A₁的坐标为（2，4），点A₂₀₂₁的坐标为（）

A、（3，﹣1） B、（﹣2，﹣2） C、（﹣3，3） D、（2，4 ）

查看试题解析
7. 我们规定：在平面直角坐标系 $x O y$ 中，任意不重合的两点 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 之间的折线距离为 $d (M ， N) = | x_{1} - x_{2} | + | y_{1} - y_{2} |$ ，例如图①中，点 $M (- 2 ， 3)$ 与点 $N (1 ， - 1)$ 之间的折线距离为 $d (M ， N) = | - 2 - 1 | + | 3 - (- 1) | = 3 + 4 = 7$ ．如图②，已知点 $P (3 ， - 4)$ 若点 $Q$ 的坐标为 $(t ， 2)$ ，且 $d (P ， Q) = 10$ ，则 $t$ 的值为（）

A、 $- 1$ B、 $5$ C、 $5$ 或 $- 13$ D、 $- 1$ 或 $7$

查看试题解析

二、填空题

8. 已知两点 $A (a ， 5)$ ， $B (0 ， b)$ 的距离为4，且直线 $A B ∥ x$ 轴，则 $b - a$ 的算术平方根为；

查看试题解析
9. 如图，在平面直角坐标系中， $x$ 轴上有一点 $A (2 ， 0)$ ，点 $A$ 第1次向上平移2个单位至点 $A_{1} (2 ， 2)$ ，接着又向左平移2个单位至点 $A_{2} (0 ， 2)$ ，然后再向上平移2个单位至点 $A_{3} (0 ， 4)$ ，向左平移2个单位至点 $A_{4} (- 2 ， 4)$ ，照此规律平移下去，点 $A$ 平移至点 $A_{2023}$ 时，点 $A_{2023}$ 的坐标是．

查看试题解析
10. 已知 $▱ A B C D$ ，三个顶点坐标为 $A (- 1 ， 2)$ 、 $B (- 2 ， - 2)$ 、 $C (3 ， - 4)$ ，则D点坐标为．

查看试题解析
11. 在平面直角坐标系中，对于任意三点A、B、C的“矩面积”，给出如下定义：“水平底” $a$ ：任意两点横坐标差的最大值，“铅垂高” $h$ ：任意两点纵坐标的最大值，则“矩面积” $S = a h$ .例如：三点坐标分别为A（1，2）、B（-3，1）、C（2，-2），则“水平底” $a$ =5，“铅垂高” $h$ =4，“矩面积”S=20.若D（1，2）、E（-2，1），F（0，t ）三点的“矩面积”S=15，则的 $t$ 值为.

查看试题解析
12. 如图，正方形ABCD的两个顶点 $A (0 ， 0)$ ， $C (6 ， 6)$ ，对正方形ABCD进行如下变换：把每个点的横、纵坐标都乘以同一个数a，将得到的点先向右平移m个单位，再向上平移n个单位（m＞0，n＞0），得到正方形 $A_{1} B_{1} C_{1} D_{1}$ ，其中B的对应点为 $B_{1} (\frac{5}{2} ， \frac{1}{3})$ ， D的对应点为 $D_{1} (\frac{1}{2} ， \frac{7}{3})$ ，若正方形ABCD内部的一个点F经过上述相同变换后得到的对应点 $F_{1}$ 与点F重合，则F点的坐标为．

查看试题解析

三、解答题

13. 对于平面直角坐标系xOy中的点P（a，b），若点P′的坐标为（a+kb，ka+b）（其中k为常数，且k≠0），
则称点P′为点P的“k属派生点”．例如：P（1，4）的“2属派生点”为P′（1+2×4，2×1+4），即P′（9，6）．

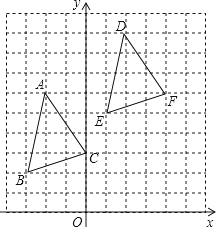
(1)、点P（﹣2，3）的“3属派生点”P′的坐标为；

(2)、若点P的“5属派生点”P′的坐标为（3，﹣9），求点P的坐标；

(3)、若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且线段PP′的长度为线段OP长度的2倍，求k的值．

查看试题解析
14.
如图，△ABC各顶点的坐标分别为A（﹣2，6），B（﹣3，2），C（0，3），将△ABC先向右平移4个单位长度，再向上平移3个单位长度，得到△DEF．
（1）分别写出△DEF各顶点的坐标；
（2）如果将△DEF看成是由△ABC经过一次平移得到的，请指出这一平移的平移方向和平移距离．

查看试题解析

四、作图题

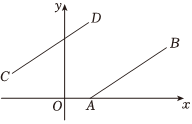
15. 如图，在平面直角坐标系中，平行于 $x$ 轴的线段AB上的所有点的纵坐标都是-1，横坐标的取值范围是1≤r≤5，则线段AB上任意一点的坐标可以用“（x，-1）（1≤r≤5）”表示，按照这样的规定，回答下列问题.

(1)、怎样表示线段CD上任意一点的坐标？

(2)、把线段AB向上平移3个单位，画出所得到的线段，线段上任意一点的坐标可以怎样表示？

(3)、把线段CD向右平移3个单位，画出所得到的线段，线段上任意一点的坐标又可以怎样表示？

查看试题解析

五、综合题

16. 在平面直角坐标系中，点 $A$ 、 $B$ 的坐标分别为 $A (a ， 0)$ ， $B (0 ， b)$ 且 $a$ ， $b$ 满足 $| a + 3 | = - \sqrt{b + 1}$ ，已知点 $C$ 坐标为 $(0 ， 4)$ ，

(1)、求 $a$ 、 $b$ 的值及 $S_{△ A B C}$ 的面积；

(2)、若点 $M$ 在坐标轴上，且 $S_{△ A C M} = \frac{1}{5} S_{△ A B C}$ ，请直接写出点 $M$ 的坐标．

查看试题解析
17. 如图所示，点 $A$ 的坐标为 $(1 ， 0)$ ，点 $B$ 的坐标为 $(0 ， 2)$ ，将三角形 $O A B$ 沿 $x$ 轴负方向平移3个单位长度，平移后的图形为三角形 $D E C$ ．

(1)、直接写出点 $C$ 的坐标；

(2)、在四边形 $A B C D$ 中，点 $P$ 从点 $B$ 出发沿 $B C - C D$ 移动，若点 $P$ 的速度为每秒1个单位长度，运动时间为 $t$ 秒，回答下列问题：
① $t =$ ▲ 秒时，点 $P$ 的横坐标与纵坐标互为相反数；

②用含有 $t$ 的式子表示点 $P$ 的坐标；

③当 $3 < t < 5$ 时，设 $∠ C B P = x °$ ； $∠ P A D = y °$ ， $∠ B P A = z °$ ，探索 $x$ ， $y$ ， $z$ 之间的数量关系，并说明理由．

查看试题解析

2023-2024学年人教版初中数学七年级下册 7.2.2 用坐标表示平移 同步分层训练 培优题

一、选择题

二、填空题

三、解答题

四、作图题

五、综合题

2023-2024学年人教版初中数学七年级下册 7.2.2 用坐标表示平移同步分层训练培优题