2023-2024学年人教版初中数学七年级下册 7.2.2 用坐标表示平移同步分层训练提升题

试卷更新日期：2024-03-19 类型：同步测试

进入出卷网下载

一、选择题

1. 若将点 $A$ 先向左平移1个单位，再向上平移4个单位，得到的 $B (- 3 ， 2)$ ，则点 $A$ 的坐标为（）

A、 $(- 2 ， 6)$ B、 $(- 4 ， 6)$ C、 $(- 2 ， - 2)$ D、 $(- 4 ， - 2)$

查看试题解析
2. 抛物线 $y = (x - 2)^{2} - 1$ 可以由抛物线 $y = x^{2}$ 平移得到，下列平移正确的是（）

A、先向左平移2个单位长度，然后向上平移1个单位长度 B、先向左平移2个单位长度，然后向下平移1个单位长度 C、先向右平移2个单位长度，然后向上平移1个单位长度 D、先向右平移2个单位长度，然后向下平移1个单位长度

查看试题解析
3. 在平面直角坐标系中，将 $△ A B C$ 各点的纵坐标保持不变，横坐标都减去3，则所得图形与原图形的关系为将原图形（）

A、向上平移3个单位 B、向下平移3个单位 C、向左平移3个单位 D、向右平移3个单位

查看试题解析
4. 下列说法中错误的是（）

A、平行于 $x$ 轴的直线上的所有点的纵坐标相同 B、平行于 $y$ 轴的直线上的所有点的横坐标相同 C、若点 $P (a ， b)$ 在 $x$ 轴上，则 $a = 0$ D、 $(- 3 ， 4)$ 与 $(4 ， - 3)$ 表示两个不同的点

查看试题解析
5. 如图，在平面直角坐标系 $x O y$ 中，四边形 $A B C O$ 是正方形，已知点 $A$ 的坐标为 $(2 ， 1)$ ，则点 $C$ 的坐标为（）

A、 $(- 1 ， 2)$ B、 $(1 ， - 2)$ C、 $(- 1 ， \sqrt{5})$ D、 $(- 2 ， 1)$

查看试题解析
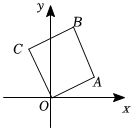6. 在如图所示的直角坐标系中， $△ A B C$ 的面积为 $2$ ，三个顶点的坐标分别为 $A (- 3 ， - 2)$ ， $B (- 1 ， - 1)$ ， $C (a ， b)$ ， $a$ 、 $b$ 均为负整数，在图中的网格中，满足条件的点 $C$ 坐标有（）

A、 $3$ 个 B、 $4$ 个 C、 $6$ 个 D、 $7$ 个

查看试题解析
7. 在平面直角坐标系 $x O y$ 中，长方形 $A B C D$ 的两条对称轴是坐标轴，邻边长分别为4，6．若点A在第一象限，则点C的坐标是（）

A、 $(- 2 ， - 3)$ B、 $(2 ， 3)$ C、 $(- 2 ， - 3) 或 (- 3 ， - 2)$ D、 $(2 ， 3) 或 (3 ， 2)$

查看试题解析

二、填空题

8. 已知 $A (3 ， y) ， B (x ， - 3)$ ，若 $A B / / x$ 轴，且线段 $A B = 5$ ，则 $x =$ ， $y =$ .

查看试题解析
9. 如图，在平面直角坐标系xOy中，线段CD是由线段AB平移得到的，B的坐标上，已知A ， C ， D三点的坐标分别为（2，1），（4，2），（3，4），则点B的坐标为．

查看试题解析
10. 在平面直角坐标系中，对于任意三个不重合的点 $A$ ， $B$ ， $C$ 的“矩面积”，给出如下定义：“水平底” $a$ 指任意两点横坐标差的最大值，“铅垂高” $h$ 指任意两点纵坐标差的最大值，“矩面积” $S = a h$ ．例如： $A (1 ， 2)$ ， $B (- 3 ， 1)$ ， $C (2 ， - 2)$ 则“水平底” $a = 5$ ， “铅垂高” $h = 4$ ， “矩面积” $S = a h = 20$ ．若 $D (1 ， 2)$ ， $E (- 2 ， 1)$ ， $F (0 ， t)$ 三点的“矩面积”为 $18$ ，则 $t$ 的值为．

查看试题解析
11. 如图，在平面直角坐标系中，已知点 $A (1 ， 1)$ ， $B (- 1 ， 1)$ ， $C (- 1 ， - 2)$ ， $D (1 ， - 2)$ ，把一根长为 $2023$ 个单位长度且没有弹性的细线 $($ 线的粗细忽略不计 $)$ 的一端固定在 $A$ 处，并按 $A \to B \to C \to D \to A \dots \dots$ 的规律紧绕在四边形 $A B C D$ 的边上，则细线的另一端所在位置的点的坐标是．

查看试题解析
12. 如图，在平面直角坐标系中，等腰直角三角形 $O A A_{1}$ 的直角边 $O A$ 在 $x$ 轴上，点 $A_{1}$ 在第一象限，且 $O A = 1$ ，以点 $A_{1}$ 为直角顶点， $O A_{1}$ 为直角边作等腰直角三角形 $O A_{1} A_{2}$ ，再以点 $A_{2}$ 为直角顶点， $O A_{2}$ 为直角边作等腰直角三角形 $O A_{2} A_{3}$ ……以此规律，则点 $A_{2018}$ 的坐标是.

查看试题解析

三、解答题

13. 如图，点A，B的坐标分别是 $(- 3 ， 1)$ ， $(- 1 ， - 2)$ ，若将线段AB平移至 $A_{1} B_{1}$ 的位置， $A_{1}$ 与 $B_{1}$ 的坐标分别是 $(m ， 4)$ 和 $(3 ， n)$ .

(1)、 $m =$ ， $n =$ .

(2)、求线段AB在平移过程中扫过的图形面积(一组对边平行且相等的四边形是平行四边形).

查看试题解析
14. 在如图所示的直角坐标系中画出点M（2，-2），N（4，-2），P（2，4），并完成下面的填空：

(1)、M，N两点的连线与横轴（填“垂直”或“平行”）．

(2)、 M，P两点的连线与纵轴（填“垂直”或“平行”。

(3)、已知点Q（4，m），若PQ∥MN，则m的值是多少？

查看试题解析

四、综合题

15. 已知平面直角坐标系中有一点 $M (m - 1 ， 2 m + 4)$ ．

(1)、若点M在x轴上，请求出点M的坐标．

(2)、若点 $N (5 ， - 1)$ ，且 $M N ∥ x$ 轴，请求出点M的坐标．

查看试题解析
16. 在平面直角坐标系中， $△ A B C$ 经过平移得到 $△ A^{'} B^{'} C^{'}$ ，位置如图所示．

(1)、分别写出点 $A$ ， $A^{'}$ 的坐标： $A$ （，）， $A^{'}$ （，）．

(2)、请说明 $△ A^{'} B^{'} C^{'}$ 是由 $△ A B C$ 经过怎样的平移得到的；

(3)、若点 $M (m ， n + 1)$ 是 $△ A B C$ 内部的一点，则平移后对应点 $M^{'}$ 的坐标为 $(- 1 ， m - 2)$ ，求 $m$ 和 $n$ 的值．

查看试题解析

2023-2024学年人教版初中数学七年级下册 7.2.2 用坐标表示平移 同步分层训练 提升题

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年人教版初中数学七年级下册 7.2.2 用坐标表示平移同步分层训练提升题