2023-2024学年人教版初中数学七年级下册 7.1.1 有序数对 同步分层训练 基础题
试卷更新日期：2024-03-19 类型：同步测试
一、选择题
-
1. 如果把电影票上“5排3座”记作 ， 那么表示（ ）A、“4排4座” B、“9排4座” C、“4排9座” D、“9排9座”2. 下列命题是假命题的是（ ）A、坐标平面内的点与有序实数对是一一对应的 B、算术平方根等于本身的数是和 C、同位角的平分线互相平行 D、在同一平面内，过一点有且只有一条直线与已知直线垂直3. 电影院里的座位按“×排×号”编排，小明的座位简记为（12，6），小菲的位置简记为（12，12），则小明与小菲坐的位置为（ ）A、同一排 B、前后同一条直线上 C、中间隔六个人 D、前后隔六排4. 如图，是象棋盘的一部分，若帅位于点（5，1）上，则炮位于点 （ ）
A、（ 1，1） B、（ 4，2） C、（ 2，1） D、（ 2，4）5. 下列五个命题：①如果两个数的绝对值相等，那么这两个数的平方相等；②内错角相等；③在同一平面内，垂直于同一条直线的两条直线互相平行；④两个无理数的和一定是无理数；⑤坐标平面内的点与有序数对是一一对应的.其中真命题的个数是（ ）
A、2个 B、3个 C、4个 D、5个6. 某电影院里排号可以用数对表示，小明买了排号的电影票，用数对可表示为（ ）A、 B、 C、 D、7. 如图，小明从点O出发，先向西走400m，再向南走300m到达点M，如果点M的位置用（-4，-3）表示，那么（1，2）表示的位置是（ ）
A、点A B、点B C、点C D、点D8. 如图是雷达在一次探测中发现的三个目标，其中目标A，B的位置分别表示为（120°，5），（240°，4），按照此方法可以将目标C的位置表示为（ ）
A、（30°，1） B、（210°，6） C、（30°，6） D、（60°，2）二、填空题
-
9. 电影院里5排2号的座位记为 ， 则表示 ．10. 春节假期期间，小刚去电影院观看《流浪地球2》，若将小刚的座位“7排11号”简记为（7，11），则同一场次“8排10号”的座位简记为 ．11. 如图所示，围棋盘的左下角呈现的是一局围棋比赛中的几手棋，为记录棋谱方便，横线用数字表示，纵线用英文字母表示，这样，黑棋❶的位置可记为（C，4），白棋②的位置可记为（E，3），则黑棋❾的位置应记为 ．
12. 早上8点钟时室外温度为2 ℃，我们记作(8，2)，则晚上9点时室外温度为零下3 ℃，我们应该记作.13. 有一个英文单词的字母顺序对应如图中的有序数对分别为（5，3），（6，3）（7，3）（4，1）（4，4）请你把这个英文单词写出来或者翻译中文为 ．
三、解答题
-
14. 如图，甲处表示两条路的交叉口，乙处也是两条路的交叉口，如果用（1，3）表示甲处的位置，那么“（1，3）→（2，3）→（3，3）→（4，3）→（4，2）→（4，1）→（4，0）”表示甲处到乙处的一种路线，若图中一个单位长度表示5km，请你用上述表示法写出甲处到乙处的另两种走法，最短距离是多少千米？
15. 如图所示，A的位置为（2，6），小明从A出发，经（2，5）→（3，5）→（4，5）→（4，4）→（5，4）→（6，4），小刚也从A出发，经（3，6）→（4，6）→（4，7）→（5，7）→（6，7），则此时两人相距几个格？
四、综合题
-
16. 观察如图所示象棋棋盘，回答下列问题：
(1)、说出“将”与“帅”的位置；(2)、说出“马3进4”（即第3列的“马”前进到第4列）后的位置．17. 如图，在5×5的方格（每小格边长为1）内有4只甲虫A、B、C、D，它们爬行规律总是先左右，再上下．规定：向右与向上为正，向左与向下为负．从A到B的爬行路线记为：A→B（＋1，＋4），从B到A的爬行路线为：B→A（－1，－4），其中第一个数表示左右爬行信息，第二个数表示上下爬行信息，那么图中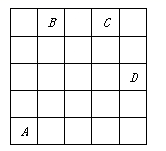
(1)、 A→C（ ， ），B→D（ ， ），C→（＋1，）；(2)、若甲虫A的爬行路线为A→B→C→D，请计算甲虫A爬行的路程；(3)、若甲虫A的爬行路线依次为（＋2，＋2），（＋1，－1），（－2，＋3），（－1，－2），最终到达甲虫P处，请在图中标出甲虫A的爬行路线示意图及最终甲虫P的位置．