2024年河北省初中毕业生升学文化课模拟考试数学试卷(四)
试卷更新日期:2024-03-19 类型:中考模拟
一、选择题
-
1. 平江某天的最高气温是 , 最低气温是 , 则该地这一天的温差是( )A、 B、 C、 D、2. 地球的海洋面积约为363000000平方米,其中数363000000用科学记数法表示为( )A、363×106 B、36.3×107 C、3.63×108 D、0.363×1093. 如图,一副三角板拼成如图所示图形,则的度数为( )
 A、120° B、60° C、105° D、75°4. 下列计算中,正确的是( )A、2= B、(1-)(1+)=-1 C、(2-)(3+)=4 D、5. 要拼一个从上面、正面、侧面看到的都是
A、120° B、60° C、105° D、75°4. 下列计算中,正确的是( )A、2= B、(1-)(1+)=-1 C、(2-)(3+)=4 D、5. 要拼一个从上面、正面、侧面看到的都是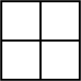 的图形,至少用多少个
的图形,至少用多少个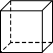 ?( ) A、5 B、6 C、7 D、86. 如图,由六个边长为的小正方形构成一个大长方形,连接小正方形的三个顶点,可得到 , 则中边上的高是( )
?( ) A、5 B、6 C、7 D、86. 如图,由六个边长为的小正方形构成一个大长方形,连接小正方形的三个顶点,可得到 , 则中边上的高是( )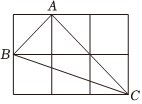 A、 B、 C、 D、7. 如图,已知平行四边形ABCD,AB≤BC.用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列做法正确的是( )A、
A、 B、 C、 D、7. 如图,已知平行四边形ABCD,AB≤BC.用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列做法正确的是( )A、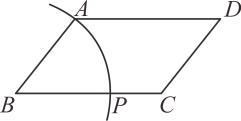 B、
B、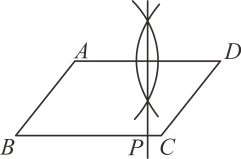 C、
C、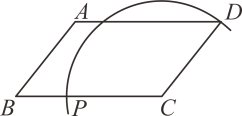 D、
D、 8. 若x3m+nyn+1÷(x5y3)·(xy)=x5y2 , 则m,n分别为( )A、m=3,n=2 B、m=2,n=2 C、m=2,n=3 D、m=3,n=19. 小明和小林在探索代数式x2+(x≠0)有没有最大(小)值时,小明做了如下探索:
8. 若x3m+nyn+1÷(x5y3)·(xy)=x5y2 , 则m,n分别为( )A、m=3,n=2 B、m=2,n=2 C、m=2,n=3 D、m=3,n=19. 小明和小林在探索代数式x2+(x≠0)有没有最大(小)值时,小明做了如下探索:∵x2++2-2 =(x+)2-2≥-2,
∴小明的结论是x2+的最小值为-2
小林做了如下探索
∵x2+-2+2 =(x-)2+2≥2,
小林的结论是x2+的最小值为2;则( )
A、小明正确 B、小林正确 C、小明和小林都正确 D、小明和小林都不正确10. 如图,点是反比例函数与的一个交点,图中阴影部分的面积为 , 则该反比例函数的表达式为( )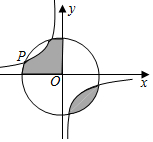 A、 B、 C、 D、11. 如图所示,某同学作了一个圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( )
A、 B、 C、 D、11. 如图所示,某同学作了一个圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( ) A、1 B、3 C、 D、12. 如图,D,E分别是△ABC的边AB,AC的中点.求证:DE∥BC,且.
A、1 B、3 C、 D、12. 如图,D,E分别是△ABC的边AB,AC的中点.求证:DE∥BC,且.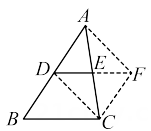
证明:延长 DE 至点 F,使 EF=DE,连结 FC,DC,AF.
又∵AE=EC,
∴四边形ADCF是平行四边形.
以下是接着的排序错误的证明步骤:
①∴DF∥BC.
②∴CF∥AD,即CF∥BD.
③∴四边形 DBCF 是平行四边形.
④∴DE∥BC,且正确的证明顺序应是( )
A、②→③→①→④ B、②→①→③→④ C、①→③→④→② D、①→③→②→④13. 学校组织学生参加知识问答,问答活动共设有20道选择题,各题分值相同,每题必答,如表记录了A、B、C三名学生的得分情况,按此规则,参赛学生D的得分可能是( ).参赛学生
答对题数
答错题数
得分
A
20
0
100
B
19
1
93
C
15
5
65
A、75 B、63 C、56 D、4414. 如图,不等边内接于 , I是其内心, , , , 内切圆半径为( ) A、4 B、 C、 D、15. 如图,五一旅游黄金周期间,某景区规定A和B为入口,C,D,E为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从A入口进入、从C,D出口离开的概率是( )
A、4 B、 C、 D、15. 如图,五一旅游黄金周期间,某景区规定A和B为入口,C,D,E为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从A入口进入、从C,D出口离开的概率是( )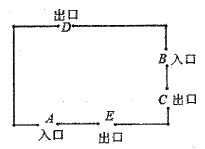 A、 B、 C、 D、16. 如图 , 动点从的顶点出发,沿匀速运动到点停止.在动点运动过程中,线段的长度与运动时间的函数关系如图所示,其中点为曲线部分的最低点,若的面积是 , 则图中的值为( )
A、 B、 C、 D、16. 如图 , 动点从的顶点出发,沿匀速运动到点停止.在动点运动过程中,线段的长度与运动时间的函数关系如图所示,其中点为曲线部分的最低点,若的面积是 , 则图中的值为( )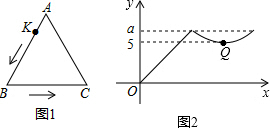 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 如图所示,在 中, , 是斜边 上的中线, 分别为 的中点,若 ,则 .
 18. 形如 的代数式(m≠n),如果交换m和n的位置,式子的值不变,我们就把这样的式子叫做完美对称式.已知关于x,y的分式是完美对称式.(1)、m=.(2)、若完美对称式满足:且x>y>0,则y=(用含x的代数式表示).19. 某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售,销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,则第二周每个旅游纪念品的销售价格为元.
18. 形如 的代数式(m≠n),如果交换m和n的位置,式子的值不变,我们就把这样的式子叫做完美对称式.已知关于x,y的分式是完美对称式.(1)、m=.(2)、若完美对称式满足:且x>y>0,则y=(用含x的代数式表示).19. 某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售,销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,则第二周每个旅游纪念品的销售价格为元.
三、解答题
-
20. 整式的值为 .(1)、当时,求的值;(2)、若某个关于的不等式的解集如图所示,为该不等式的一个解,求的负整数值;
 (3)、关于的不等式组恰有两个整数解,求的取值范围.21. 目前,某城市“一户一表”居民用电实行阶梯电价,具体收费标准如下.
(3)、关于的不等式组恰有两个整数解,求的取值范围.21. 目前,某城市“一户一表”居民用电实行阶梯电价,具体收费标准如下.一户居民一个月用电量(单位:度)
电价(单位:元/度)
第1档
不超过180度的部分
0.5
第2档
超过180度的部分
0.7
(1)、若该市某户12月用电量为200度,该户应交电费元;(2)、若该市某户12月用电量为x度,请用含x的代数式分别表示和时该户12月应交电费多少元;(3)、若该市某户12月应交电费125元,则该户12月用电量为多少度?22. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气”.某校响应号召,开展了“读红色经典,传革命精神”为主题的读书活动,学校对本校学生五月份阅读该主题相关书籍的读书量进行了随机抽样调查,并对所有随机抽取的学生的读书量(单位:本)进行了统计.根据调查结果,绘制了不完整的统计表和扇形统计图.
读书量
本
本
本
本
本
人数
人
人
人
人
 (1)、本次调查共抽取学生人,学生读书量的众数是 , 中位数是 , 扇形统计图中“本”部分所对应的圆心角的度数为;(2)、求该样本中平均每人的读书量;(3)、已知该校有名学生,请估计该校学生中,五月份读书量不少于“本”的学生人数.(4)、后来又抽取几名学生的读书量,他们的读书量都不低于本,把这几名学生的读书量与原来的数据一起统计中位数没有发生改变,则最多又抽取名学生.23. 如图 , 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 已知点 .
(1)、本次调查共抽取学生人,学生读书量的众数是 , 中位数是 , 扇形统计图中“本”部分所对应的圆心角的度数为;(2)、求该样本中平均每人的读书量;(3)、已知该校有名学生,请估计该校学生中,五月份读书量不少于“本”的学生人数.(4)、后来又抽取几名学生的读书量,他们的读书量都不低于本,把这几名学生的读书量与原来的数据一起统计中位数没有发生改变,则最多又抽取名学生.23. 如图 , 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 已知点 .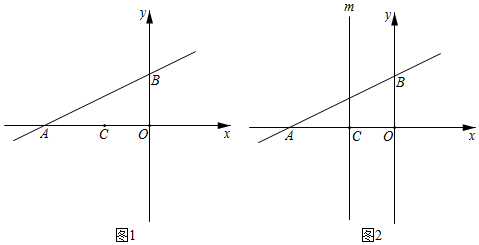 (1)、求出点 , 点的坐标.(2)、是直线上一动点,且和的面积相等,求点坐标.(3)、如图 , 过点作平行于轴的直线 , 在直线上是否存在点 , 使得是等腰直角三角形?若存在,请直接写出所有符合条件的点的坐标;若不存在,请说明理由.24. 操作探究题(1)、已知是半圆的直径,(是正整数,且不是3的倍数)是半圆的一个圆心角.
(1)、求出点 , 点的坐标.(2)、是直线上一动点,且和的面积相等,求点坐标.(3)、如图 , 过点作平行于轴的直线 , 在直线上是否存在点 , 使得是等腰直角三角形?若存在,请直接写出所有符合条件的点的坐标;若不存在,请说明理由.24. 操作探究题(1)、已知是半圆的直径,(是正整数,且不是3的倍数)是半圆的一个圆心角.操作:如图1,分别将半圆的圆心角(取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);

交流:当时,可以仅用圆规将半圆的圆心角所对的弧三等分吗?
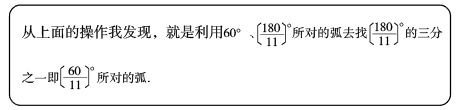
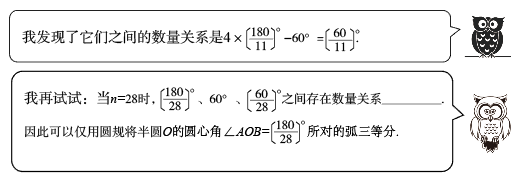
探究:你认为当满足什么条件时,就可以仅用圆规将半圆的圆心角所对的弧三等分?说说你的理由.
(2)、如图2,的圆周角 . 为了将这个圆的圆周14等分,请作出它的一条14等分弧(要求:仅用圆规作图,不写作法,保留作图痕迹).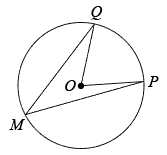 25. 科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽路空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系如图所示;小钢球离地面高度(米)与它的运动时间(秒)之间的函数关系如图中抛物线所示.
25. 科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽路空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系如图所示;小钢球离地面高度(米)与它的运动时间(秒)之间的函数关系如图中抛物线所示.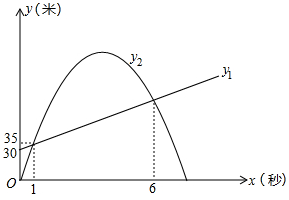 (1)、直接写出与之间的函数关系式;(2)、求出与之间的函数关系式;(3)、小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?26. 在中, , , , 点是的中点四边形是菱形按逆时针顺序排列 , , 且 , 菱形可以绕点旋转,连接和 , 设直线和直线所夹的锐角为 .
(1)、直接写出与之间的函数关系式;(2)、求出与之间的函数关系式;(3)、小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?26. 在中, , , , 点是的中点四边形是菱形按逆时针顺序排列 , , 且 , 菱形可以绕点旋转,连接和 , 设直线和直线所夹的锐角为 .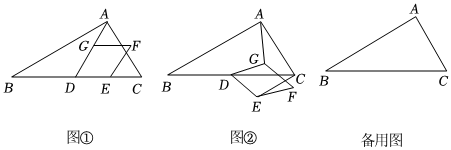 (1)、在菱形绕点旋转的过程中,当点在线段上时,如图 , 请直接写出与的数量关系及的值;(2)、当菱形绕点旋转到如图所示的位置时,中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、设直线与直线的交点为 , 在菱形绕点旋转一周的过程中,当所在的直线经过点时,请直接写出的面积.
(1)、在菱形绕点旋转的过程中,当点在线段上时,如图 , 请直接写出与的数量关系及的值;(2)、当菱形绕点旋转到如图所示的位置时,中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、设直线与直线的交点为 , 在菱形绕点旋转一周的过程中,当所在的直线经过点时,请直接写出的面积.