人教版初中数学九年级下学期 第二十八章 锐角三角函数 单元测试 B卷
试卷更新日期:2024-03-19 类型:单元试卷
一、选择题
-
1. 如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是( )
 A、 B、 C、 D、2. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= , 反比例函数y=的图象经过点C,与AB交于点D,若△COD的面积为30,则k的值等于( )
A、 B、 C、 D、2. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= , 反比例函数y=的图象经过点C,与AB交于点D,若△COD的面积为30,则k的值等于( )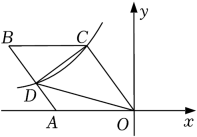 A、﹣48 B、48 C、﹣36 D、﹣183. 如图,正六边形的边长是1cm,则线段AB和CD之间的距离为( )
A、﹣48 B、48 C、﹣36 D、﹣183. 如图,正六边形的边长是1cm,则线段AB和CD之间的距离为( ) A、2 cm B、 cm C、 cm D、1cm4. 如图,某学习小组为测量学校A与河对岸凉亭B之间的距离,在学校附近选一点C,利用测量仪器测得∠C=90°,∠A=α,AC=4km.据此,可求得学校与凉亭之间的距离AB等于 ( )
A、2 cm B、 cm C、 cm D、1cm4. 如图,某学习小组为测量学校A与河对岸凉亭B之间的距离,在学校附近选一点C,利用测量仪器测得∠C=90°,∠A=α,AC=4km.据此,可求得学校与凉亭之间的距离AB等于 ( ) A、4sinαkm B、 C、 D、4tanαkm5. 如图,在地面上的点A处测得树顶B的仰角为a , 米,则树高为( )
A、4sinαkm B、 C、 D、4tanαkm5. 如图,在地面上的点A处测得树顶B的仰角为a , 米,则树高为( ) A、米 B、米 C、米 D、 米6. 等腰三角形的底边长为 , 周长为 , 则底角的正切值是( )A、 B、 C、 D、无法确定7. 由小正方形组成的网格如图,A,B,C三点都在格点上,则∠ABC的正切值为( )
A、米 B、米 C、米 D、 米6. 等腰三角形的底边长为 , 周长为 , 则底角的正切值是( )A、 B、 C、 D、无法确定7. 由小正方形组成的网格如图,A,B,C三点都在格点上,则∠ABC的正切值为( )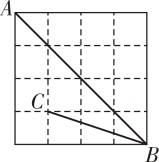 A、 B、 C、 D、8. 如图,在矩形中, , , 将沿射线平移a个单位长度()得到 , 连接 , , 则当是直角三角形时,a的值为( )
A、 B、 C、 D、8. 如图,在矩形中, , , 将沿射线平移a个单位长度()得到 , 连接 , , 则当是直角三角形时,a的值为( ) A、或 B、2或 C、或 D、或39. 如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )
A、或 B、2或 C、或 D、或39. 如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )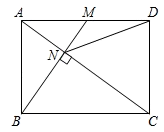 A、①②③④ B、①②③ C、①②④ D、②③④10. 如图,在矩形中,交于点 , 点在上,连接分别交 , 于点 , . 若 , 则的值是( )
A、①②③④ B、①②③ C、①②④ D、②③④10. 如图,在矩形中,交于点 , 点在上,连接分别交 , 于点 , . 若 , 则的值是( )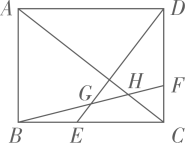 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
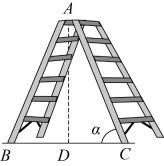
11. 已知中, , , , 那么的长是 .12. 人字梯为现代家庭常用的工具.如图,若 , 的长都为 , 当时,人字梯顶端离地面的高度为 . (结果保留小数点后1位)(参考数据:)
 13. 如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,则车位所占的宽度EF为米.( , 结果精确到0.1)
13. 如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,则车位所占的宽度EF为米.( , 结果精确到0.1) 14. 如图,点D是等边△ABC内部的一点,∠ADC=120°,AB2=19, , 则线段BD的长度是 .
14. 如图,点D是等边△ABC内部的一点,∠ADC=120°,AB2=19, , 则线段BD的长度是 .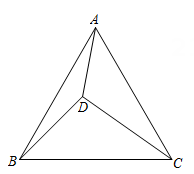 15. 如图,在中, , 分别以和为边向外作正方形和正方形 , 过点作的延长线的垂线,垂足为点 . 连接 , 交的延长线于点 . 下列说法:①;②若 , , 则;③;④;⑤若 , , 则的面积为 , 正确的有 . (填序号)
15. 如图,在中, , 分别以和为边向外作正方形和正方形 , 过点作的延长线的垂线,垂足为点 . 连接 , 交的延长线于点 . 下列说法:①;②若 , , 则;③;④;⑤若 , , 则的面积为 , 正确的有 . (填序号)
三、解答题
-
16. 如图1,某款线上教学设备由底座,支撑臂 , 连杆 , 悬臂和安装在处的摄像头组成.如图2是该款设备放置在水平桌面上的示意图,已知支撑臂 , , 固定 , 可通过调试悬臂与连杆的夹角提高拍摄效果.
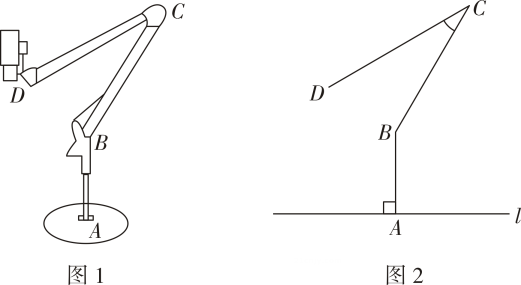 (1)、当悬臂与桌面平行时,=°(2)、问悬臂端点到桌面的距离约为多少?(3)、已知摄像头点到桌面的距离为30cm时拍摄效果较好,那么此时悬臂与连杆的夹角的度数约为多少?(参考数据:)17. 如图,航母由西向东航行,到达A处时,测得小岛C位于它的北偏东60°方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛C位于它的北偏东37°方向,如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.参考数据:sin37°≈0.6,cos37°≈0.80,tan37°≈0.75
(1)、当悬臂与桌面平行时,=°(2)、问悬臂端点到桌面的距离约为多少?(3)、已知摄像头点到桌面的距离为30cm时拍摄效果较好,那么此时悬臂与连杆的夹角的度数约为多少?(参考数据:)17. 如图,航母由西向东航行,到达A处时,测得小岛C位于它的北偏东60°方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛C位于它的北偏东37°方向,如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.参考数据:sin37°≈0.6,cos37°≈0.80,tan37°≈0.75 18. 如图,是的直径,点在上,点为的中点,过点作的切线,交延长线于点 , 连接交于点 .
18. 如图,是的直径,点在上,点为的中点,过点作的切线,交延长线于点 , 连接交于点 .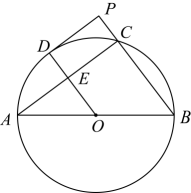 (1)、求证:四边形是矩形;(2)、作射线交的延长线于点F , 若 , , 求的长.
(1)、求证:四边形是矩形;(2)、作射线交的延长线于点F , 若 , , 求的长.四、实践探究题
-
19. 【问题情境】
在综合实践活动课上,李老师让同桌两位同学用相同的两块含的三角板开展数学探究活动,两块三角板分别记作和 , 设 .
【操作探究】
如图1,先将和的边、重合,再将绕着点A按顺时针方向旋转,旋转角为 , 旋转过程中保持不动,连接 .
 (1)、当时,;当时,;(2)、当时,画出图形,并求两块三角板重叠部分图形的面积;(3)、如图2,取的中点F,将绕着点A旋转一周,点F的运动路径长为 .20. 问题:如何设计“倍力桥”的结构?
(1)、当时,;当时,;(2)、当时,画出图形,并求两块三角板重叠部分图形的面积;(3)、如图2,取的中点F,将绕着点A旋转一周,点F的运动路径长为 .20. 问题:如何设计“倍力桥”的结构?图1是搭成的“倍力桥”,纵梁a,c夹住横梁 , 使得横梁不能移动,结构稳固.图2是长为 , 宽为3cm的横梁侧面示意图,三个凹槽都是半径为1cm的半圆,圆心分别为 , 纵梁是底面半径为1cm的圆柱体,用相同规格的横梁、纵梁搭“桥”,间隙忽略不计.
探究1:

(1)、图3是“桥”侧面示意图,A,B为横梁与地面的交点,C,E为圆心,是横梁侧面两边的交点,测得 , 点到AB的距离为12cm,试判断四边形的形状,并求的值.(2)、若搭成的“桥”刚好能绕成环,其侧面示意图的内部形成一个多边形.①若有12根横梁绕成环,图4是其侧面示意图,内部形成十二边形 , 求的值;
②若有根横梁绕成的环(为偶数,且 , 试用关于的代数式表示内部形成的多边形的周长.
21. 阅读素材,完成任务.测试机器人行走路径
素材一
图1是某校科技兴趣小组设计的一个可以帮助餐厅上菜的机器人,该机器人能根据指令要求进行旋转和行走.如图为机器人所走的路径.机器人从起点出发,连续执行如下指令:机器人先向前直行(表示第次行走的路程),再逆时针旋转 , 直到第一次回到起点后停止.记机器人共行走的路程为 , 所走路径形成的封闭图形的面积为S .

素材二
如图2,当每次直行路程均为1(即),时,机器人的运动路径为 , 机器人共走的路程 , 由图2图3易得所走路径形成的封闭图形的面积为 .

素材三
如图4,若 , 机器人执行六次指令后回到起点处停止.
解决问题
任务
固定变量
探索变量
探索内容
任务一
直行路程
旋转角度与路程
任务二
旋转角度
直行路程
若 , 求与的值.
任务三
旋转角度 , 路程
路径形成的封闭图形面积S .
若 , 请直接写出与之间的数量关系,并求出当S最大时的值.
五、综合题
-
22. 在菱形中, , 点是射线上一动点,以为一边向右侧作等腰 , 使 , , 点的位置随着点的位置变化而变化.
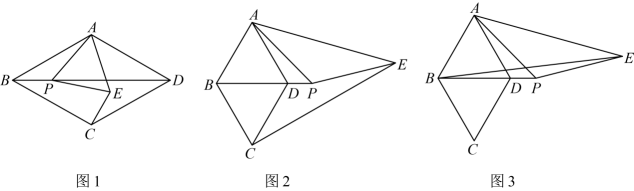 (1)、如图 , 若 , 当点在菱形内时,连接 , 与的数量关系是 , 与的位置关系是;(2)、若 , 当点在线段的延长线上时,
(1)、如图 , 若 , 当点在菱形内时,连接 , 与的数量关系是 , 与的位置关系是;(2)、若 , 当点在线段的延长线上时,①如图 , 与有何数量关系,与有何位置关系?请说明理由;
②如图 , 连接 , 若 , , 求线段的长.
23. 如图①,将一个正方形纸片和一个等腰直角三角形纸片放入平面直角坐标系中,点 , 点 , , . 如图②,将纸片绕点顺时针旋转,设旋转角为 . (1)、当旋转角为30°时,求此时点E的坐标;(2)、当旋转角为时,连接 , 求的值.(3)、在旋转的过程中,当最大时,求此时的面积(直接写出结果即可).
(1)、当旋转角为30°时,求此时点E的坐标;(2)、当旋转角为时,连接 , 求的值.(3)、在旋转的过程中,当最大时,求此时的面积(直接写出结果即可).