2023-2024学年初中数学人教版九年级下学期 第二十八章 锐角三角函数 单元测试 A卷
试卷更新日期:2024-03-19 类型:单元试卷
一、选择题
-
1. 在等腰△ABC中,AB=AC=4,BC=6,那么cosB的值是A、 B、 C、 D、2. 如图,在中, , 下列结论中正确的是( )
 A、 B、 C、 D、3. 从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°,则船离灯塔的水平距离是( )A、42米 B、14米 C、21米 D、42米4. 如图1是第七届国际数学教育大会(ICME)会徽,选择其中两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC,sin∠AOB= , 则tanC的值为( )
A、 B、 C、 D、3. 从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°,则船离灯塔的水平距离是( )A、42米 B、14米 C、21米 D、42米4. 如图1是第七届国际数学教育大会(ICME)会徽,选择其中两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC,sin∠AOB= , 则tanC的值为( ) A、 B、 C、 D、5. 如图,在中, , , , 则下列结论正确的是( )
A、 B、 C、 D、5. 如图,在中, , , , 则下列结论正确的是( ) A、 B、 C、 D、6. 图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,和分别是两根不同长度的支撑杆,其中两支脚 , 展开角 , 晾衣臂 , 则支樟杆的端点离地面的高度为( )
A、 B、 C、 D、6. 图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,和分别是两根不同长度的支撑杆,其中两支脚 , 展开角 , 晾衣臂 , 则支樟杆的端点离地面的高度为( )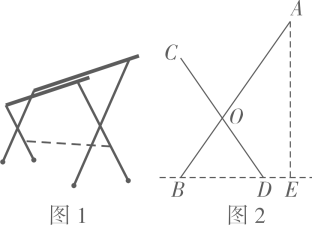 A、 B、 C、 D、7. 如图是的高, , , , 则的长为( ).
A、 B、 C、 D、7. 如图是的高, , , , 则的长为( ).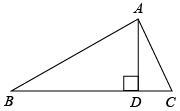 A、 B、 C、 D、8.
A、 B、 C、 D、8.如图,已知AB是⊙O的直径,CD是弦且CD⊥AB,BC=6,AC=8,则sin∠ABD的值是( )
 A、 B、 C、 D、9. 在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A、 B、 C、 D、9. 在Rt△ABC中,各边都扩大5倍,则∠A的三角函数值( )
A、不变 B、扩大5倍 C、缩小5倍 D、不能确定10. 如图,四边形ABCD是的内接四边形, , , , , 则AD的长为( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
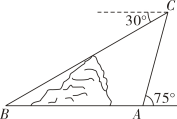
11. 在Rt△ABC中,∠C=90°,AC=5,BC=12,则sinA=12. 如图,小山的东侧炼A处有一个热气球,由于受西风的影响,以30(米/分)的速度沿与地面成75°角的方向飞行,20分后到达点C处,此时热气球上的人测得小山西侧点B处的俯角为30°,则小山东西两侧A,B两点间的距离为米(结果保留根号).
 13. 如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是 .
13. 如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是 .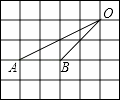 14. 若 为锐角,且 ,则 °.15. 某水库大坝横截面示意图如下所示,其中AB,CD分别表示水库下底面、上底面的水平线,∠ABC=120°,BC的长是50m,则水库大坝的高度h=.
14. 若 为锐角,且 ,则 °.15. 某水库大坝横截面示意图如下所示,其中AB,CD分别表示水库下底面、上底面的水平线,∠ABC=120°,BC的长是50m,则水库大坝的高度h=.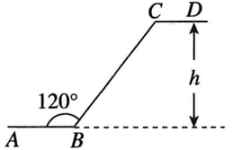
三、解答题
-
16. 如图所示,无人机在生活中的使用越来越广泛,小明用无人机测量大楼的高度.无人机悬停在空中处,测得楼楼顶的俯角是 , 楼的楼顶的俯角是 , 已知两楼间的距离米,楼的高为10米,从楼的处测得楼的处的仰角是、、、、在同一平面内).
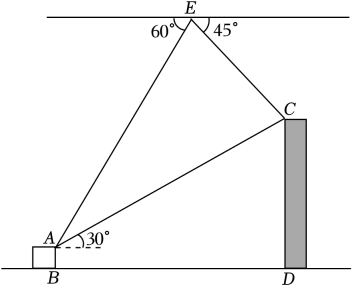 (1)、求楼的高;(2)、小明发现无人机电量不足,仅能维持60秒的飞行时间,为了避免无人机掉落砸伤人,站在点的小明马上控制无人机从处匀速以5米秒的速度沿方向返航,无人机能安全返航吗?17. 如图, 在 Rt 中, 是 A C 边上一点, 连接 B D, E 是 外一点且满足 平分 , 连接 D E 交 A B 于点 .
(1)、求楼的高;(2)、小明发现无人机电量不足,仅能维持60秒的飞行时间,为了避免无人机掉落砸伤人,站在点的小明马上控制无人机从处匀速以5米秒的速度沿方向返航,无人机能安全返航吗?17. 如图, 在 Rt 中, 是 A C 边上一点, 连接 B D, E 是 外一点且满足 平分 , 连接 D E 交 A B 于点 . (1)、求证:四边形ADBE是菱形;(2)、连接OC,若四边形ADBE的周长为20, , 求 O C 的长18. 为建设美好公园社区, 增强民众生活幸福感, 如图 1, 某社区服务中心在文化活动室墙外安装遮阳篷, 便于社区居民休想. 在如图 2 的侧面示意图中, 遮阳篷靠墙端离地高记为 B C, 遮阳篷 A B 长为 5 米, 与水平面的夹角为 .
(1)、求证:四边形ADBE是菱形;(2)、连接OC,若四边形ADBE的周长为20, , 求 O C 的长18. 为建设美好公园社区, 增强民众生活幸福感, 如图 1, 某社区服务中心在文化活动室墙外安装遮阳篷, 便于社区居民休想. 在如图 2 的侧面示意图中, 遮阳篷靠墙端离地高记为 B C, 遮阳篷 A B 长为 5 米, 与水平面的夹角为 .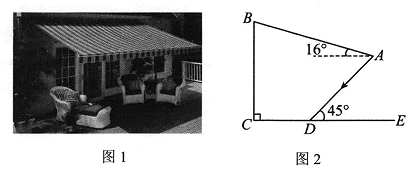 (1)、求点A到墙面BC的距离;(2)、当太阳光线AD与地面CE的夹角为45°时,量得影长CD为1.8米,求遮阳篷靠墙端离地高BC的长.(结果精确到0.1米;参考数据: sin16°≈0.28,cos16°≈0.96,tan16° ≈0.29 )
(1)、求点A到墙面BC的距离;(2)、当太阳光线AD与地面CE的夹角为45°时,量得影长CD为1.8米,求遮阳篷靠墙端离地高BC的长.(结果精确到0.1米;参考数据: sin16°≈0.28,cos16°≈0.96,tan16° ≈0.29 )四、实践探究题
-
19. 仁皇阁是一个著名景点,某校九年级研学期间参观了仁皇阁,数学兴趣小组对仁皇阁高度产生了浓厚的兴趣,他们想运用所学知识估算出仁皇阁的高度。
课题 估算仁皇阁高度 
测量工具 测量角度的仪器,皮尺,刻度尺等 组别 测量方案示意图 测量方案说明 组1 
如图1 , 先在仁皇阁底部广场的C处用仪器测得阁楼顶端A的仰角为27° , 然后从C处向阁楼底部前进10m到达D处,此时在D处测得阁楼顶端A的仰角为30° . 组2 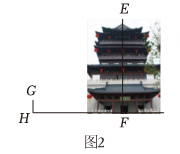
如图2 , 身高1.5m的组员站在仁皇阁正门边上合影.打印出照片后量得此组员图上高度GH为0.5cm,量得仁皇阁图上高度EF为12.9cm. (1)、任务一 请分别计算两组中测量得到的阁楼高度;(结果保留小数点后一位.参考数据)(2)、任务二 后续经过查证后发现小组2数据更为精确,请你帮小组1分析可能产生误差的原因.(写出一条即可)20. 阅读材料,回答问题:小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b= ,AB=c=2,那么 = =2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着 = = 的关系.
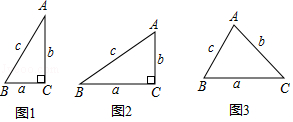
这个关系对于一般三角形还适用吗?为此他做了如下的探究:
(1)、如图2,在R△ABC中,∠C=90°,BC=a,AC=b,AB=C,请判断此时“ = = ”的关系是否成立?(2)、完成上述探究后,他又想“对于任意的锐角△ABC,上述关系还成立吗?”因此他又继续进行了如下的探究:如图3,在锐角△ABC中,BC=a,AC=b,AB=c,请判断此时“ = = ”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).21. 阅读材料:关于三角函数还有如下的公式:
Sin(α±β)=sinαcosβ±cosαsinβ
tan(α±β)=
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,
例:tan15°=tan(45°﹣30°)
=
=
=
根据以上阅读材料,请选择适当的公式解答下面的问题
(1)、计算sin15°;(2)、我县体育场有一移动公司的信号塔,小明想利用所学的数学知识来测量该塔的高度,小华站在离塔底A距离7米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.62米,请帮助小华求出该信号塔的高度.(精确到0.1米,参考数据: ≈1.414)
五、综合题
-
22. 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对().如图,在中, , 顶角A的正对记作 , 这时.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述对角的正对定义,解下列问题:
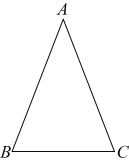 (1)、 的值为( ).A、 B、1 C、 D、2(2)、对于 , 的正对值的取值范围是.(3)、已知 , 其中α为锐角,试求的值.23. 如图,已知AB是⊙O的直径,C为⊙O上一点,∠OCB的角平分线交⊙O于点D,F在直线AB上,且 , 垂足为E,连接AD,BD.
(1)、 的值为( ).A、 B、1 C、 D、2(2)、对于 , 的正对值的取值范围是.(3)、已知 , 其中α为锐角,试求的值.23. 如图,已知AB是⊙O的直径,C为⊙O上一点,∠OCB的角平分线交⊙O于点D,F在直线AB上,且 , 垂足为E,连接AD,BD. (1)、求证:DF是⊙O的切线;(2)、若 , ⊙O的半径为4,求BF的长.
(1)、求证:DF是⊙O的切线;(2)、若 , ⊙O的半径为4,求BF的长.