2023-2024学年初中数学人教版八年级下学期第二十章数据的分析单元测试 B卷

试卷更新日期：2024-03-19 类型：单元试卷

进入出卷网下载

一、选择题

1. 一组由小到大排列的数据为 $- 1$ ， 0，4， $x$ ， 6，16，这组数据的中位数为5，则这组数据的众数可能是 $($ 　　 $)$

A、5 B、6 C、 $- 1$ D、5.5

查看试题解析
2. 5名学生投篮训练，规定每人投10次，记录他们每人投中的次数，得到五个数据，经分析这五个数据的中位数为6，唯一众数是7，则他们投中次数占投篮总次数的百分率可能是（）

A、40% B、56% C、60% D、62%

查看试题解析
3. 某班准备从甲、乙、丙、丁四名同学中选一名最优秀的同学参加校编程大赛，下表记录了四人3次选拔测试的相关数据：

甲
乙
丙
丁
平均分
95
93
95
94
方差
3.2
3.2
4.8
5.2
根据表中数据，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 如图是根据某店今年6月 1日至5日每天的用水量(单位：吨)绘制成的折线统计图.下列结论正确的是（）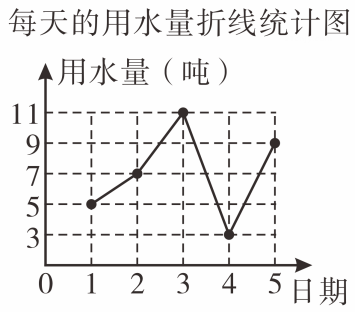

A、平均数是6 B、众数是7 C、中位数是 11 D、方差是8

查看试题解析
5. 已知一组数据x₁，x₂，x₃，平均数是2，方差是3，则另一组数2x₁-1，2x₂-1，2x₃-1的平均数和方差分别是（）

A、2， $\frac{2}{3}$ B、3，3 C、3，12 D、3，4

查看试题解析
6. 某班37名同学中只有1名同学的身高是165cm.若除甲、乙外其余35名同学身高的平均数和中位数都是165 cm，则该班37名同学身高的平均数a和中位数b不可能是（）

A、a>165 cm，b=165 cm B、a<165 cm，b=165 cm C、a<165 cm，b=164 cm D、a=165 cm，b=166 cm

查看试题解析
7. 有下列说法：①数据7，7，6，5，4的众数是2；②若数据 $x_{1} ， x_{2} ， \dots ， x_{n}$ 的平均数是 $\bar{x}$ ，则 $(x_{1} - \bar{x}) + (x_{2} - \bar{x}) + \dots + (x_{n} - \bar{x}) = 0 ；$ ③数据1，2，3，4，5，6的中位数是3和4；④数据21，22，23，24，25的方差是2.其中正确的是（）

A、①③ B、②④ C、①②④ D、②③④

查看试题解析
8. 某地积极号召居民节约用水，为了解居民用水情况，在一个小区随机抽查了10户家庭的月用水量，将统计结果绘制为如图所示的条形统计图，则下列关于这10户家庭的月用水量(单位：吨)的说法正确的是（）
某小区10户家庭的月用水量条形统计图

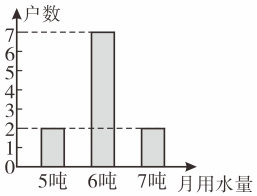A、众数是5吨 B、中位数是 6吨 C、平均数是7吨 D、方差是 8 吨²

查看试题解析
9. 某“中学生暑期环保小组”的同学，随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量，数据如下（单位：只）：6，5，7，8，7，5，8，10，5，9，利用上述数据估计该小区2 000户家庭一周内需要环保方便袋（）只.

A、2000 B、14000 C、28000 D、98000

查看试题解析
10. 某一公司共有51名员工（其中包括1名经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（）

A、平均数增加，中位数不变 B、平均数和中位数不变 C、平均数不变，中位数增加 D、平均数和中位数均增加

查看试题解析

二、填空题

11. 若一组数据4，5，6，4，4，7，x，5的平均数是5，则众数是.

查看试题解析
12. 若一组数据1，2，4，6，x的中位数和平均数相等，则x的值是.

查看试题解析
13. 学校进行广播操比赛，20 位评委给某班的评分情况统计图如图所示，则该班的平均分是分.
广播操比赛某班评分情况统计图

查看试题解析
14. 教练对跳远运动员小刚的训练效果进行了测试，6次跳远的成绩(单位：m)如下：7.6，7.8，7.7，7.8，8.0，7.9.这6次成绩的平均数是7.8m，方差是 $\frac{1}{60}$ m².若小刚再跳两次，成绩分别是7.7，7.9，则小刚这8次跳远成绩的方差将(填“变大”“变小”或“不变”).

查看试题解析
15. 已知数据 $x_{1}$ ， $x_{2}$ ， $\dots$ ， $x_{n}$ 的方差是 $0.1$ ，则 $4 x_{1} - 2$ ， $4 x_{2} - 2$ ， $\dots$ ， $4 x_{n} - 2$ 的方差为.

查看试题解析

三、解答题

16. 某公司为提高服务质量，对其某个部门开展了客户满意度问卷调查，客户满意度以分数呈现，满意度从低到高为1分，2分，3分，4分，5分，共5档公司规定：若客户所评分数的平均数或中位数低于3.5分，则该部门需要对服务质量进行整改．工作人员从收回的问卷中随机抽取了20份，如图是根据这20份问卷中的客户所评分数绘制的统计图．

(1)、求客户所评分数的中位数平均数，并判断该部门]是否需要整改．

(2)、监督人员从余下的问卷中又随机抽取了1份，与之前的20份合在一起，重新计算后，发现客户所评分数的平均数大于3.55分，求监督人员抽取的问卷所评分数为几分．与(1)相比，中位数是否发生变化？

查看试题解析
17. 甲乙两名同学进行射击训练，在相同条件下各射靶5次，成绩统计如表：
命中环数
7
8
9
10
甲命中相应环数的次数
2
2
0
1
乙命中相应环数的次数
1
3
1
0

(1)、计算甲、乙两人的射击成绩的平均数；

(2)、若从甲、乙两人射击成绩方差的角度评价两人的射击水平，请通过计算说明：谁的射击成绩更稳定些？

查看试题解析
18. 商店里有A，B 两种糖果，A种糖果的单价为a 元/千克，B种糖果的单价为b元/千克，且a≠b.商店准备用这两种糖果混合制成若干种什锦糖，什锦糖的定价方法是：若取m千克A 种糖果和n千克B 种糖果混合制成什锦糖，则什锦糖的售价定为总价除以总质量，即 $\frac{m a + n b}{m + n}$

(1)、某种什锦糖由 A，B两种糖果按质量比1：3混合制成，求该种什锦糖的售价.

(2)、现有甲、乙两种什锦糖，均由A，B两种糖果混合制成，其中甲什锦糖由相同质量的 A，B两种糖果混合制成；乙什锦糖由相同总价的A，B两种糖果混合制成，则甲、乙两种什锦糖的售价分别为多少？

(3)、选择合适的方法比较（2）中甲、乙两种什锦糖的售价哪个更高？

查看试题解析

四、实践探究题

19. 甲、乙两支运动队各有10名队员，他们的年龄分布情况分别如图、表所示：

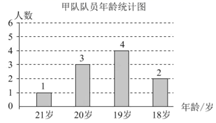
甲、乙两队队员年龄统计表

平均数（近似值）

众数

中位数

甲队

a

①

②

乙队

20

③

b

解决下列问题：

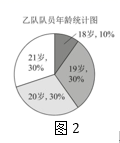
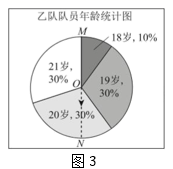
(1)、求甲队队员的平均年龄a的值．（结果取整数）

(2)、补全统计表中的①②③三处．

(3)、阅读理解-----扇形图中求中位数的方法．
[阅读与思考]

小明同学在求乙队队员年龄的中位数b时，是这样思考的：因为中位数是将一组数据按大小排序后，排在中间位置的一个数或中间两个数的平均数，那就需要先找到数据按大小排序后，大致排在50%附近的数，再根据中位数的概念进行细化求解．

图2这个扇形图中的数据18~21是按大小顺序旋转排列的，我们就可以像图3所示的这样，先找到最大数据“21”与最小数据“18”的分界半径OM，为找到排在50%附近的数，再作出直径MN，那么射线ON指向的数据就是中位数．

王老师的评价：小明的这个方法是从中位数的概念出发，充分利用了扇形图的特性形象直观地解决问题．

[理解与应用]

请你利用小明的方法直接写出统计表中b的值．

查看试题解析

五、综合题

20. 为了了解某校初中各年级学生每天的平均睡眠时间（单位： $h$ ），精确到1h ，抽样调查了部分学生，并用得到的数据绘制了下面两幅不完整的统计图．
请你根据图中提供的信息，回答下列问题：

(1)、求出扇形统计图中百分数 $a$ 的值为，所抽查的学生人数为．

(2)、求出平均睡眠时间为8小时的人数，并补全频数分布直方图．

(3)、求出这部分学生的平均睡眠时间的众数和平均数．

(4)、如果该校共有学生1200名，请你估计睡眠不足（少于）8小时的学生数．

查看试题解析
21. 2023年3月5日，中华人民共和国第十四届全国人民代表大会第一次会议在北京召开，某校为使学生更好地了解“两会”，争做新时代好少年，开展了“两会”知识竞赛活动，分别从八（1）班和八（2）班各随机抽取10名学生的竞赛成绩（单位：分，满分100分），并对数据进行了如下分析与整理：
收集数据
八（1）班学生知识竞赛成绩：84，75，82，70，91，83，80，74，79，82
八（2）班学生知识竞赛成绩：80，65，75，68，95，82，84，80，92，79
分析数据

平均数/分
中位数/分
众数/分
方差
八（1）班
80
b
82
31.6
八（2）班
a
80
c
78.4
根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ， $c =$ ．

(2)、请你对八（1）班和八（2）班抽取的这10名学生的知识竞赛成绩作出评价．

(3)、该校除开展两会知识竞赛活动外，还组织了制作关于“两会”手抄报的评比活动，并对手抄报进行评分（单位：分，满分100分）．在八（2）班抽取的这10名学生中，甲同学和乙同学的知识竞赛成绩分别为95分和92分，手抄报成绩分别为70分和80分．现对甲同学和乙同学进行综合评分，若知识竞赛成绩占70%，手抄报成绩占30%，则哪位同学的综合成绩较好？

查看试题解析
22. 某社区为了解辖区群众对新冠疫情防控相关知识的知晓情况，通过发放问卷进行测评，从中随机抽取20份问卷，并统计成绩（成绩得分用x表示，单位：分），收集数据如下：
88 92 95 99 85 91 86 92 100 95 94 94 88 94 95 97 82 100 99 94
整理数据：

          $80 \leq x < 85$
          $85 \leq x < 90$
          $90 \leq x < 95$
          $95 \leq x \leq 100$
1
4
a
8
分析数据：

平均数
中位数
众数
93
b
94
根据以上信息，解答下列问题：

(1)、a= ， b=；

(2)、该社区有2000名群众参加了此次问卷测评活动，请估计成绩不低于90分的人数；

(3)、请从平均数和众数中选择一个量，结合本题解释它的意义．

查看试题解析
23. 学校举办纪念“五四运动”104周年暨“青春心向党，建功新时代”演讲比赛．同学们用青春的声音和故事，激扬五四精神，彰显青春风采，展现拼搏风貌，深情地演绎了对党和祖国的热爱之情．

初赛阶段两个年级各10名选手的成绩统计如下：
七年级：98　96　86　85　84　94　77　69　59　94
八年级：99　96　73　82　96　79　65　96　55　96
他们的数据分析过程如下：

(1)、整理、描述数据：根据上面得到的两组数据，分别绘制频数分布直方图如图：

请补全八年级频数分布直方图；

(2)、数据分析：两组数据的平均数、中位数、方差如表所示：
年级
平均数
中位数
方差
七年级
①
85.5
144.36
八年级
83.7
②
251.21
根据以上数据求出表格中①，②两处的数据；

(3)、推断结论：根据以上信息，判断哪个年级比赛成绩整体较好？说明理由（至少从两个不同角度说明判断的合理性）．

查看试题解析

命中环数	7	8	9	10
甲命中相应环数的次数	2	2	0	1
乙命中相应环数的次数	1	3	1	0

	平均数（近似值）	众数	中位数
甲队	a	①	②
乙队	20	③	b

	平均数/分	中位数/分	众数/分	方差
八（1）班	80	b	82	31.6
八（2）班	a	80	c	78.4

$80 \leq x < 85$	$85 \leq x < 90$	$90 \leq x < 95$	$95 \leq x \leq 100$
1	4	a	8

年级	平均数	中位数	方差
七年级	①	85.5	144.36
八年级	83.7	②	251.21

	甲	乙	丙	丁
平均分	95	93	95	94
方差	3.2	3.2	4.8	5.2

2023-2024学年初中数学人教版八年级下学期 第二十章 数据的分析 单元测试 B卷

一、选择题

二、填空题

三、解答题

四、实践探究题

五、综合题

2023-2024学年初中数学人教版八年级下学期第二十章数据的分析单元测试 B卷