2023-2024学年初中数学人教版八年级下学期第二十章数据的分析单元测试 A卷

试卷更新日期：2024-03-19 类型：单元试卷

进入出卷网下载

一、选择题

1. 样本数据2、 $a$ 、3、4的平均数是3，则 $a$ 的值是 $($ 　　 $)$

A、1 B、2 C、3 D、4

查看试题解析
2. 某篮球队10名队员的年龄如下表所示：
年龄(岁)
18
19
20
21
人数
2
4
3
1
这10名队员年龄的众数(单位：岁)和中位数(单位：岁)分别是（）

A、19，19 B、19，19.5 C、20，19 D、20，19.5

查看试题解析
3. 某校在计算学生的数学学期总评成绩时，规定期中考试成绩占40%，期末考试成绩占60%.如果小林同学的数学期中考试成绩为80分，期末考试成绩为90分，那么他的数学学期总评成绩是（）

A、8 0分 B、82分 C、84分 D、86分

查看试题解析
4. 在一次献爱心的捐款活动中，某班50名同学的捐款金额如图所示，则在这次捐款活动中，该班同学捐款金额的平均数是（）

A、14.2元 B、15元 C、16.2元 D、20.25元

查看试题解析
5. 甲、乙、丙、丁四个城市连续四年的平均降水量相仿，年降水量的方差分别是 $S_{甲}^{2} = 67.5 ， S_{乙}^{2} = 204 ，$ $S_{丙}^{2} = 145 ， S_{丁}^{2} = 50 ，$ 这四个城市年降水量最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 在射击训练中，某队员的10次射击成绩如图，则这10次射击成绩的中位数(单位：环)和众数(单位：环)分别是（）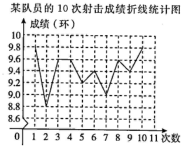

A、9.6，9.6 B、9.5，9.4 C、9.5，9.6 D、9.6，9.8

查看试题解析
7. 期中考试后，班里有两位同学议论他们小组的数学成绩，小晖说：“我们组考分是 82 分的人最多”，小聪说：“我们组的7 位同学成绩排在最中间的恰好也是 82分”.上面两位同学的话中能反映出的统计量分别是（）

A、众数和平均数 B、平均数和中位数 C、平均数和众数 D、众数和中位数

查看试题解析
8. 下表是某校乐团的年龄分布，其中一个数据被遮盖了.下列说法中，正确的是（）
年龄(岁) 13 14 15 16
频数 5 7 13 ■

A、中位数可能是 14 B、中位数可能是 14.5 C、平均数可能是 14 D、众数可能是 16

查看试题解析

二、填空题

9. 4月 23日是世界读书日，某校当天举行了演讲大赛，演讲得分按“演讲内容”占 40%，“语言表达”占40%，“形象风度”占 10%，“整体效果”占 10%进行计算，小芳这四项的得分依次为85，88，92，90，则她的最后得分是分.

查看试题解析
10. 在一次广场舞比赛中，甲、乙两个队参加表演的队员的身高(单位：cm)分别是：
甲队：163 165 165 164 168
乙队：162 164 164 167 168
甲队队员身高的方差为cm²，(填“甲”或“乙”)队队员的身高更整齐.

查看试题解析
11. 为了解“睡眠管理”落实情况，某校随机调查了46名学生每天平均睡眠时间，并将样本数据绘制成如图所示的统计图(其中有两个数据被遮盖).有以下关于睡眠时间的统计量：①平均数，②中位数，③众数，④方差，其中与被遮盖的数据无关的是(填序号).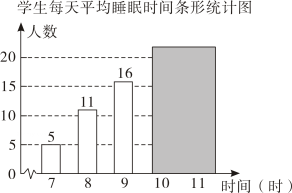

查看试题解析
12. 学校要从王静、李玉两同学中选拔1人参加运动会志愿者工作，选拔项目为普通话、体育知识和旅游知识，并将成绩依次按4：3：3记分.两人的各项选拔成绩如表所示，则最终胜出的同学是.

普通话
体育知识
旅游知识
王静
80
90
70
李玉
90
80
70

查看试题解析
13. 某单位招聘员工，其中一位应聘者的笔试成绩是90分，面试成绩是80分，若笔试成绩与面试成绩在综合成绩中的权重分别是 $70 %$ ， $30 %$ ，则该应聘者的综合成绩为分．

查看试题解析

三、解答题

14. 某校学生会要在甲、乙两位候选人中选择一人担任文艺部干事，对他们进行了文化水平艺术水平组织能力的测试，根据综合成绩择优录取，他们的各项成绩(单项满分100分)如下表所示：
候选人
文化水平
艺术水平
组织能力
甲
80分
87分
82分
乙
80分
96分
76分

(1)、如果把各项成绩的平均数作为综合成绩，应该录取谁？

(2)、如果想录取一名组织能力较强的候选人，把文化水平、艺术水平、组织能力三项成绩分别按照20%，20%，60%的比例计人综合成绩，应该录取谁？

查看试题解析
15. 为提高学生的数学思维能力，某中学开展“迎元旦数学知识竞赛”，八(1)班、八(2)班各选出5名选手参加竞赛，整理5名选手的竞赛成绩(满分为100分)绘制如图所示的统计图和不完整的统计表．

平均数
中位数
众数
八(1)班(分)
87

80
八(2)班(分)

85

(1)、请你把表格补充完整；

(2)、结合两班竞赛成绩的平均数中位数和众数，你认为哪个班的竞赛成绩较好；

(3)、计算两个班竞赛成绩的方差，并说明哪个班的成绩较为整齐．

查看试题解析
16. 某校对八年级400名学生进行了一次体育测试，并随机抽取甲、乙两个班各50名学生的测试成绩(成绩均为整数，满分为50分)进行整理、描述和分析，制成了如下统计图表(用x表示成绩，数据分成5组：A：30≤x<34，B：34≤x<38，C：38≤x<42，D：42≤x<46，E：46≤x≤50).
班级
甲班
乙班
平均分
44.1
44.1
中位数
44.5
n
众数
m
42
方差
7.7
17.4
乙班成绩在D组的具体分数是42，42，42，42，42，42，42，42，42，42，43，44，45，45.
根据以上信息，回答下列问题：

(1)、求m，n的值.

(2)、小明这次的测试成绩是43分，在班上排名属中游略偏上，小明是甲、乙哪个班的学生?请说明理由.

(3)、假设该校八年级学生都参加此次测试，成绩达到45分及45分以上为优秀，请通过优秀率估计该校本次测试成绩优秀的学生人数.

查看试题解析

四、实践探究题

17. “双碳”背景下，新能源汽车在主流的大众消费群体中越来越受欢迎

.

在会展中心举行一场新能源汽车车展活动中，共有三十几种不同品牌的新能源汽车参展，根据不同续航程将这些车分成六组，统计结果如下：

分组	$A$	$B$	$C$	$D$	$E$	$F$
$($ 单位：公里 $)$	$x \leq 400$	$400 < x \leq 500$	$500 < x \leq 600$	$600 < x \leq 700$	$700 < x \leq 800$	$x > 800$
数量 $($ 单位：辆 $)$	$40$	$120$	$132$	$95$	$68$	$45$

(1)、在参展的新能源汽车中，续航里程在组的车最多；续航里程的中位数落在组；

(2)、小渡家看中了售价一样的甲、乙两款汽车，根据汽车鉴定机构发布的数据对这两款车的续航里程、百公里加速、智能化水平三项性能进行了打分

(

百分制

)

，如下表：

	续航里程 $($ 分 $)$	百公里加速 $($ 分 $)$	智能化水平 $($ 分 $)$
甲车	$82$	$90$	$100$
乙车	$80$	$100$	$90$

小渡将续航里程、百公里加速、智能化水平三项性能的得分按 $5$ ： $2$ ： $3$ 的比例确定甲、乙两款汽车的最终得分，并以此为依据做出了选择，你知道小渡的选择是什么吗？请写出计算过程进行说明．

查看试题解析

18. 当前各国都高度重视人工智能并视其为提升国家竞争力的重要力量，随着人工智能与各个垂直领域的不断深入融合，普通公民也越来越需要具备人工智能的基本知识和应用能力，人工智能逐步成为中小学重要教学内容之一，某同学设计了一款机器人，为了了解它的操作技能情况，对同一设计动作与人工进行了比赛，机器人和人工各操作

10

次，测试成绩

(

百分制

)

如下：

分析数据，得到下列表格．

	平均数	中位数	众数	方差
机器人	$92$	$a$	$95$	$c$
人工	$89$	$90$	$b$	$108.8$

根据以上信息，解答下列问题：

(1)、填空：

a =

，

b =

，

c =

．

(2)、若成绩

90

分及以上为优秀，请你估计机器人操作

800

次，优秀次数为多少？

(3)、根据以上数据分析，请你写出机器人在操作技能方面的优点

. (

写一条即可

)

查看试题解析

19. 为了倡导“节约用水，从我做起”，县政府决定对机关300户家庭的用水情况作一次调查，调查小组随机抽查了其中某些家庭一年的月平均用水量（单位：吨），调查中发现，每户用水量每月均在10－14吨范围，并将调查结果制成了如图所示的条形统计图（不完整）和扇形统计图．

(1)、请将条形统计图补充完整；

(2)、这些家庭月用水量数据的平均数是，众数是，中位数是；

(3)、根据样本数据，估计机关300户家庭中月平均用水量不超过12吨的约有多少户？

查看试题解析

五、综合题

20. 某校开展了全校教师学习党史活动并进行了党史知识竞赛．从七、八年级中各随机抽取了20名教师，统计这部分的竞赛成绩．相关数据统计、整理如下：
抽取的七年级教师的竞赛成绩（单位：分）
6，7，7，8，8，8，8，8，8，8，8，9，9，9，9，10，10，10，10，10．
七八年级教师竞赛成绩统计表
年级
七年级
八年级
平均数
$\bar{x}$
$8.5$
中位数
$a$
9
众数
8
$b$
根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ．

(2)、求所抽取的七年级教师竞赛成绩的平均数 $\bar{x}$ ．

(3)、估计该校七年级120名教师中竞赛成绩达到8分及以上人数．

查看试题解析

21. 某校开学初对七年级学生进行一次安全知识问答测试，设成绩为

x

分（

x

为整数），将成绩评定为优秀、良好、合格、不合格四个等级（优秀、良好、合格、不合格分别用A、B、C、D表示），A等级：

90 \leq x \leq 100

， B等级：

80 \leq x < 90

， C等级：

60 \leq x < 80

， D等级：

0 \leq x < 60

．该校随机抽取了一部分学生的成绩进行调查，并绘制成如图不完整的统计图表．

等级	频数（人数）
A $(90 \leq x \leq 100)$	$a$
B $(80 \leq x < 90)$	16
C $(60 \leq x < 80)$	$c$
D $(0 \leq x < 60)$	4

请你根据统计图表提供的信息解答下列问题：

(1)、上表中的

a =

，

c =

，

m =

；

(2)、这组数据的中位数所在的等级是；

(3)、该校决定对分数低于80分的学生进行安全再教育，已知该校七年级共有1000名学生，求该校七年级需要进行安全再教育的学生有多少人？

查看试题解析

候选人	文化水平	艺术水平	组织能力
甲	80分	87分	82分
乙	80分	96分	76分

班级	甲班	乙班
平均分	44.1	44.1
中位数	44.5	n
众数	m	42
方差	7.7	17.4

年级	七年级	八年级
平均数	$\bar{x}$	$8.5$
中位数	$a$	9
众数	8	$b$

年龄(岁)	18	19	20	21
人数	2	4	3	1

年龄(岁)	13	14	15	16
频数	5	7	13	■

	普通话	体育知识	旅游知识
王静	80	90	70
李玉	90	80	70

2023-2024学年初中数学人教版八年级下学期 第二十章 数据的分析 单元测试 A卷

一、选择题

二、填空题

三、解答题

四、实践探究题

五、综合题

2023-2024学年初中数学人教版八年级下学期第二十章数据的分析单元测试 A卷