人教版初中数学八年级下学期 第十九章 一次函数 单元测试 B卷
试卷更新日期:2024-03-19 类型:单元试卷
一、选择题
-
1. 已知点 , , 在同一个函数图象上,这个函数图象可以是( )A、
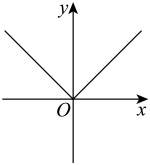 B、
B、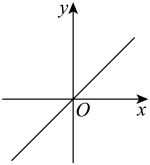 C、
C、 D、
D、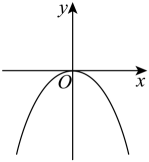 2. 如图,直线y=ax+b(a≠0)过点A(0,3),B(4,0),则不等式ax+b>0的解集是( )
2. 如图,直线y=ax+b(a≠0)过点A(0,3),B(4,0),则不等式ax+b>0的解集是( )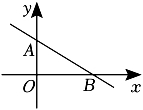 A、x>4 B、x<4 C、x>3 D、x<33. 甲无人机从地面起飞,乙无人机从距离地面20高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:)与无人机上升的时间x(单位:s)之间的关系如图所示,时,两架无人机的高度差为( )A、10 B、15 C、20 D、254. 直线y=﹣ax+a与直线y=ax在同一坐标系中的大致图象可能是( )A、
A、x>4 B、x<4 C、x>3 D、x<33. 甲无人机从地面起飞,乙无人机从距离地面20高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:)与无人机上升的时间x(单位:s)之间的关系如图所示,时,两架无人机的高度差为( )A、10 B、15 C、20 D、254. 直线y=﹣ax+a与直线y=ax在同一坐标系中的大致图象可能是( )A、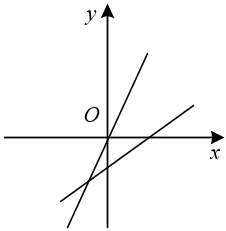 B、
B、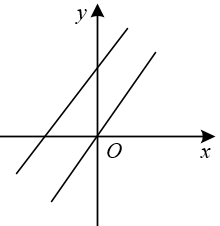 C、
C、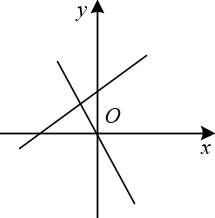 D、
D、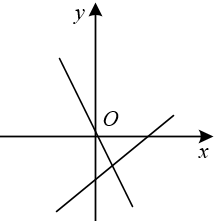 5. 一次函数与的图象如图所示,则下列说法不正确的是( )
5. 一次函数与的图象如图所示,则下列说法不正确的是( )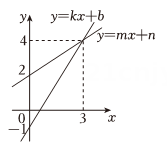 A、 B、这两个函数的图象与轴围成的三角形的面积为4. 5 C、关于的方程组的解为 D、当从0开始增加时,函数比的值先达到36. 已知点和点在直线上,则( )A、 B、 C、 D、无法判定7. 关于函数 , 给出下列说法正确的是:( )
A、 B、这两个函数的图象与轴围成的三角形的面积为4. 5 C、关于的方程组的解为 D、当从0开始增加时,函数比的值先达到36. 已知点和点在直线上,则( )A、 B、 C、 D、无法判定7. 关于函数 , 给出下列说法正确的是:( )①当时,该函数是一次函数;
②若点在该函数图象上,且 , 则;
③若该函数不经过第四象限,则;
④该函数恒过定点 .
A、①②④ B、①③④ C、②③④ D、①②③8. 有一个装有水的容器,如图所示.容器内的水面高度是10cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2cm的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是( )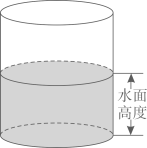 A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系9. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点 , , 点P是对角线OB上的一个动点, , 当最短时,点P的坐标为( )
A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系9. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点 , , 点P是对角线OB上的一个动点, , 当最短时,点P的坐标为( ) A、 B、 C、 D、10. 如图所示,直线y=x+3分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )
A、 B、 C、 D、10. 如图所示,直线y=x+3分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )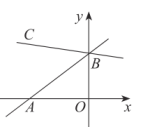 A、y=x+3 B、y=x+3 C、y=x+3 D、y=x+3
A、y=x+3 B、y=x+3 C、y=x+3 D、y=x+3二、填空题
-
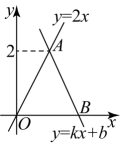
11. 直线与直线相交于点 , 则关于的方程组的解为 .12. 如图,函数的图象经过点B(3,0),与函数的图象交于点A , 则不等式0<的解集为 .
 13. 在平面直角坐标系中,一次函数y=3x﹣1与y=ax(a≠0)的图象的交点坐标是(1,2),则方程组的解是 .14. 在如图所示的平面直角坐标系中,点是直线上的动点, , 是轴上的两点,当取最小值时, .
13. 在平面直角坐标系中,一次函数y=3x﹣1与y=ax(a≠0)的图象的交点坐标是(1,2),则方程组的解是 .14. 在如图所示的平面直角坐标系中,点是直线上的动点, , 是轴上的两点,当取最小值时, .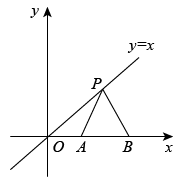 15. 在平面直角坐标系中,正方形A1B1C1O、正方形A2B2C2C1、正方形A3B3C3C2、正方形A4B4C4C3、…、正方形AnBn∁nCn-1按如图所示的方式放置,其中点A1 , A2 , A3 , A4 , …,An均在一次函数y=kx+b的图象上,点C1 , C2 , C3 , C4 , …,∁n均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为 .
15. 在平面直角坐标系中,正方形A1B1C1O、正方形A2B2C2C1、正方形A3B3C3C2、正方形A4B4C4C3、…、正方形AnBn∁nCn-1按如图所示的方式放置,其中点A1 , A2 , A3 , A4 , …,An均在一次函数y=kx+b的图象上,点C1 , C2 , C3 , C4 , …,∁n均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为 .
三、解答题
-
16. 如图,已知直线的图象经过点 , , 且与x轴交于点C .(1)、求直线的解析式;(2)、求的面积.17. 现代营养学家用身体质量指数衡量人体胖瘦程度,这个指数等于人体体重()与人体身高(m)平方的商.对于成年人来说,身体质量指数低于18.5,体重过轻;身体质量指数在18.5~25范围内,体重适中;身体质量指数高于25,体重超重或肥胖.(1)、设一个人的体重为w(),身高为h(m),则他的身体质量指数p为 . (用含w , h的式子表示)(2)、李老师的身高是 , 体重是 , 他的体重是否适中?18. 如图,直线与轴,轴分别交于A,B两点,点的坐标为.在轴的负半轴上有一点 , 直线AB上有一点 , 且OD
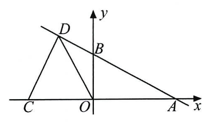 (1)、求b的值及点的坐标.(2)、在线段AB上有一个动点 , 点的横坐标为 , 作点关于轴的对称点 , 当点落在内(不包括边界)时,求的取值范围.
(1)、求b的值及点的坐标.(2)、在线段AB上有一个动点 , 点的横坐标为 , 作点关于轴的对称点 , 当点落在内(不包括边界)时,求的取值范围.四、实践探究题
-
19. 先阅读下列材料,然后解决问题:
【阅读感悟】
在平面直角坐标系中,已知点 , 当t的值发生改变时,点Q的位置也会发生改变,为了求点Q运动所形成的图象的解析式,令点Q的横坐标x , 纵坐标y , 得到了方程组消去t , 得 , 即 , 可以发现,点随t的变化而运动所形成的图象的解析式是 .
(1)、【尝试应用】观察下列四个点的坐标,不在函数图象上的是____.
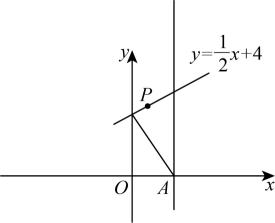
A、 B、 C、 D、(2)、求点随t的变化而运动所形成的图象的解析式;(3)、【综合运用】如图,在平面直角坐标系中,点P在一次函数的图象上运动.已知点为定点,连接 , 过点A作直线 , 且 , 求点B随点P的变化而运动所形成的图象的解析式.
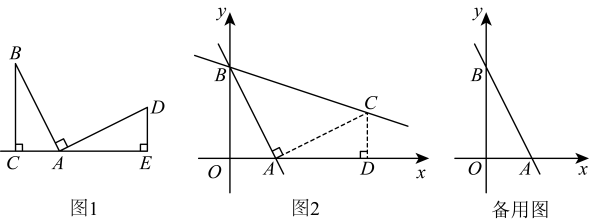
 20. 【模型介绍】
20. 【模型介绍】如图 , , , 过点作于点 , 过点作于点 . 则 . 我们把这个数学模型称为“字”模型或“一线三等角”模型.
【模型应用】
在平面直角坐标系中,直线与轴交于点 , 与轴交于点 .
(1)、如图 , 将直线绕点逆时针旋转 , 得到直线 , 求直线的表达式.下面是小明的想法,请你帮助完成.小明想利用“一线三等角”模型解决这个问题.如图,过点作的垂线交于点 , 再过点作轴的垂线,垂足为 , 可求出点的坐标为 , 从而求得直线的表达式为 .
(2)、若将直线绕点顺时针旋转 , 所得直线的表达式为 .(3)、点是线段上的一个动点,点是线段上一动点,若是等腰直角三角形,且 , 则点的坐标是 .五、综合题
-
21. 在平面直角坐标系中,正比例函数的图象经过点 , 过点A的直线与x轴、y轴分别交于B , C两点.
 (1)、求正比例函数的表达式;(2)、若的面积为的面积的倍,求直线的表达式;(3)、在(2)的条件下,在线段上找一点D , 使平分 , 求点D的坐标.22. 如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)、求正比例函数的表达式;(2)、若的面积为的面积的倍,求直线的表达式;(3)、在(2)的条件下,在线段上找一点D , 使平分 , 求点D的坐标.22. 如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.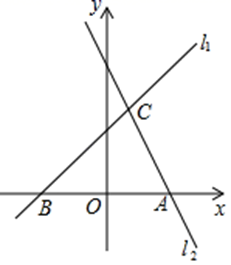 (1)、求直线l2的解析式;(2)、点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.(3)、在x轴上是否存在点P,使以B、C、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.23. 如图,在平面直角坐标系中,点 , 点C在y轴的负半轴上,连接 , 满足 .
(1)、求直线l2的解析式;(2)、点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.(3)、在x轴上是否存在点P,使以B、C、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.23. 如图,在平面直角坐标系中,点 , 点C在y轴的负半轴上,连接 , 满足 . (1)、求直线的解析式;(2)、已知直线经过点B .
(1)、求直线的解析式;(2)、已知直线经过点B .①若点D为直线上一点,若 , 求点D的坐标;
②过点O作直线 , 若点M、N分别是直线和上的点,且满足 . 请问是否存在这样的点 , 使得为直角三角形?若存在,请求出点N的坐标;若不存在,请说明理由.