人教版初中数学八年级下学期 第十九章 一次函数 单元测试 A卷
试卷更新日期:2024-03-19 类型:单元试卷
一、选择题
-
1. 直线与x轴的交点坐标是( )A、 B、 C、 D、2. 一次函数的图象是由的图象平移得到的,则移动方法为( )A、向右平移个单位 B、向左平移个单位 C、向上平移个单位 D、向下平移个单位3. 点在正比例函数的图象上,则的值为( )A、 B、 C、 D、4. 一次函数的图象如图所示,则值可能是( )
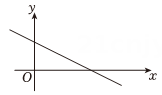 A、2 B、 C、 D、5. 如图,在平面直角坐标系中,、两点在一次函数的图象上,其坐标分别为 , , 下列结论正确的是( )
A、2 B、 C、 D、5. 如图,在平面直角坐标系中,、两点在一次函数的图象上,其坐标分别为 , , 下列结论正确的是( ) A、 , B、 , C、 , D、6. 已知一次函数 图象上的三点 , , ,则 , , 的大小关系是( )A、 B、 C、 D、7. 一种弹簧秤最大能称10kg的物体,不挂物体时弹簧的长为12cm,每挂重1kg物体,弹簧伸长0.5cm.在弹性限度内,挂重后弹簧的长度y(cm)关于所挂物体的质量x(kg)的函数表达式为( )
A、 , B、 , C、 , D、6. 已知一次函数 图象上的三点 , , ,则 , , 的大小关系是( )A、 B、 C、 D、7. 一种弹簧秤最大能称10kg的物体,不挂物体时弹簧的长为12cm,每挂重1kg物体,弹簧伸长0.5cm.在弹性限度内,挂重后弹簧的长度y(cm)关于所挂物体的质量x(kg)的函数表达式为( ) A、y=12-0.5x B、y=12+0.5x C、y=10+0.5x D、y=0.5x8. 在平面直角坐标系中,若 , , 则一次函数的图象大致是( )A、
A、y=12-0.5x B、y=12+0.5x C、y=10+0.5x D、y=0.5x8. 在平面直角坐标系中,若 , , 则一次函数的图象大致是( )A、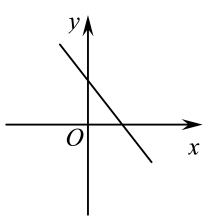 B、
B、 C、
C、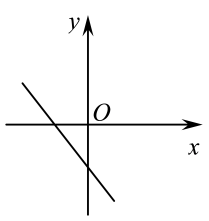 D、
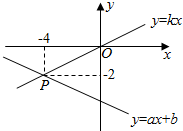
D、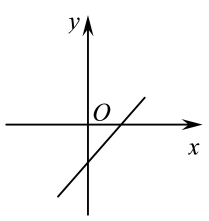 9. 如图,一次函数与的图象相交于点 , 则关于 , 的二元一次方程组的解是( )
9. 如图,一次函数与的图象相交于点 , 则关于 , 的二元一次方程组的解是( ) A、 B、 C、 D、10. 甲、乙两车从地出发,匀速驶往地.乙车出发h后,甲车才沿相同的路线开始行驶.甲车先到达地并停留分钟后,又以原速按原路线返回,直至与乙车相遇.图中的折线段表示从开始到相遇止,两车之间的距离与甲车行驶的时间x(h)的函数关系的图象,则( )
A、 B、 C、 D、10. 甲、乙两车从地出发,匀速驶往地.乙车出发h后,甲车才沿相同的路线开始行驶.甲车先到达地并停留分钟后,又以原速按原路线返回,直至与乙车相遇.图中的折线段表示从开始到相遇止,两车之间的距离与甲车行驶的时间x(h)的函数关系的图象,则( ) A、甲车的速度是 B、 , 两地的距离是 C、乙车出发4.5h时甲车到达地 D、甲车出发4.5h最终与乙车相遇
A、甲车的速度是 B、 , 两地的距离是 C、乙车出发4.5h时甲车到达地 D、甲车出发4.5h最终与乙车相遇二、填空题
-
11. 一次函数y=(2m-6)x+5中,y随x的增大而减小,则m的取值范围是 .12. 已知x﹣2y=2,且x>1,y<0,令m=x+2y , 则m的取值范围是 .13. 已知一次函数 , 它的图象经过第一、二、四象限,则 .14. 如图,已知直线和直线交于点 , 则关于 , 的二元一次方程组的解是 .
 15. 如图1,11月10日晚,“深爱万物”—2023深圳人才嘉年华活动正式启动,千余架无人机在深圳人才公园上空上演“天空之舞”,为人才喝彩、向人才致敬.如图2的平面直角坐标系中,线段分别表示1号、2号无人机在队形变换中飞行高度 , 与飞行时间的函数关系,其中 , 线段与相交于点P , 轴于点B , 点A的横坐标为25.则在第秒时1号和2号无人机在同一高度.
15. 如图1,11月10日晚,“深爱万物”—2023深圳人才嘉年华活动正式启动,千余架无人机在深圳人才公园上空上演“天空之舞”,为人才喝彩、向人才致敬.如图2的平面直角坐标系中,线段分别表示1号、2号无人机在队形变换中飞行高度 , 与飞行时间的函数关系,其中 , 线段与相交于点P , 轴于点B , 点A的横坐标为25.则在第秒时1号和2号无人机在同一高度.
三、解答题
-
16. 已知一条钢筋长90cm,把它折弯成一个等腰三角形框,其底边长记为x(cm),腰长记为y(cm).(1)、求y关于x的函数表达式和自变量x的取值范围.(2)、当x=40时,求函数y的值,并求出此时等腰三角形的面积.17. 为了响应国家提倡的“节能环保”号召,某公司研发出一款新能源纯电动车,如图是这款电动车充满电后,蓄电池剩余电量(千瓦时)关于已行驶路程(千米)的函数图象.
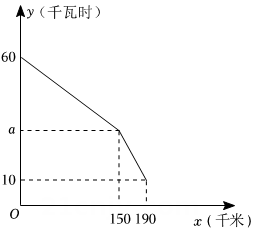 (1)、当时,1千瓦时的电量新能源纯电动车能行驶的路程为5千米,则;(2)、当时,求关于的函数表达式;(3)、请计算当新能源纯电动车已行驶160千米时,蓄电池的剩余电量.18. 如图,在平面直角坐标系中,直线AB交轴于点(4,0),交轴于点(0,3).
(1)、当时,1千瓦时的电量新能源纯电动车能行驶的路程为5千米,则;(2)、当时,求关于的函数表达式;(3)、请计算当新能源纯电动车已行驶160千米时,蓄电池的剩余电量.18. 如图,在平面直角坐标系中,直线AB交轴于点(4,0),交轴于点(0,3). (1)、求直线的解析式;(2)、是轴上一点,当的面积为5时,求点的坐标.
(1)、求直线的解析式;(2)、是轴上一点,当的面积为5时,求点的坐标.四、实践探究题
-
19. 小明观察到一个水龙头因损坏而不断地向外滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如表的一组数据:
时间t(分钟)
1
2
3
4
5
***
总水量y(毫升)
7
12
17
22
27
…
(1)、探究:根据上表中的数据,请判断和y=kt+b(k,b为常数,k≠0)哪一个能正确反映总水量y与时间t的函数关系,并求出y关于t的函数表达式.(2)、应用:①请你估算小明在第20分钟测量时量筒的总水量是多少毫升.
②一个人一天大约饮用1500毫升水,请你估算这个水龙头一个月(按30天计)的漏水量可供一人饮用多少天.
20. 小明观察到一个水龙头因损坏而不断地向外滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如下表的一组数据:时间(分钟)
1
2
3
4
5
总水量(毫升)
7
12
17
22
27
(1)、探究:根据上表中的数据,请判断总水量与时间的符合怎样的函数关系?并求出关于的表达式;(2)、应用:①请你估算小明在第20分钟测量时量筒的总水量是多少毫升?
②一个人一天大约饮用1500毫升水,请你估算这个水龙头一个月(按30天计)的漏水量可供一人饮用多少天.
五、综合题
-
21. 如图,在平面直角坐标系中,直线与坐标轴相交于点 , , 点是轴上一点.
 (1)、求直线的表达式.(2)、如图1,连接 , 将沿翻折至 , 若点恰好落在直线上,求点的坐标.(3)、如图2,点在轴的正半轴上,连接 , 将绕点顺时针旋转至的位置,连接 , 请问有最小值吗?如果有,请求出来;如果没有,请说明理由.22. 如图,直线L1: 与 轴, 轴分别交于A,B两点,点P( ,3)为直线AB上一点,另一直线L2: 经过点P.
(1)、求直线的表达式.(2)、如图1,连接 , 将沿翻折至 , 若点恰好落在直线上,求点的坐标.(3)、如图2,点在轴的正半轴上,连接 , 将绕点顺时针旋转至的位置,连接 , 请问有最小值吗?如果有,请求出来;如果没有,请说明理由.22. 如图,直线L1: 与 轴, 轴分别交于A,B两点,点P( ,3)为直线AB上一点,另一直线L2: 经过点P. (1)、求点A、B坐标;(2)、求点P坐标和 的值;(3)、若点C是直线L2与 轴的交点,点Q是 轴上一点,当△CPQ的面积等于3时,求出点Q的坐标23. 小嘉骑自行车从家出发沿公路匀速前往新华书店,小嘉妈妈骑电瓶车从新华书店出发沿同一条路回家。线段与折线分别表示两人离家的距离(km)与小嘉的行驶时间(h)之间的函数关系的图象,请解决以下问题.
(1)、求点A、B坐标;(2)、求点P坐标和 的值;(3)、若点C是直线L2与 轴的交点,点Q是 轴上一点,当△CPQ的面积等于3时,求出点Q的坐标23. 小嘉骑自行车从家出发沿公路匀速前往新华书店,小嘉妈妈骑电瓶车从新华书店出发沿同一条路回家。线段与折线分别表示两人离家的距离(km)与小嘉的行驶时间(h)之间的函数关系的图象,请解决以下问题. (1)、求的函数表达式;(2)、求点的坐标;(3)、设小嘉和妈妈两人之间的距离为(km),当时,求的取值范围.
(1)、求的函数表达式;(2)、求点的坐标;(3)、设小嘉和妈妈两人之间的距离为(km),当时,求的取值范围.