人教版初中数学八年级下学期 第十八章 平行四边形 单元测试 B卷
试卷更新日期:2024-03-19 类型:单元试卷
一、选择题
-
1. 下列说法正确的是( )A、四边相等的四边形是正方形 B、对角线互相垂直且相等的四边形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直平分的四边形是菱形2. 已知菱形的边长为13cm , 它的一条对角线长为10cm , 则该菱形的面积为( )A、60cm2 B、120cm2 C、240cm2 D、480cm23. 菱形、矩形、正方形都具有的性质是( )A、两组对边分别平行且相等 B、对角线相等 C、四条边相等,四个角相等 D、对角线互相垂直4. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( )
 A、1 B、 C、 D、5. 如图,菱形中,连接 , 若 , 则的度数为( )
A、1 B、 C、 D、5. 如图,菱形中,连接 , 若 , 则的度数为( )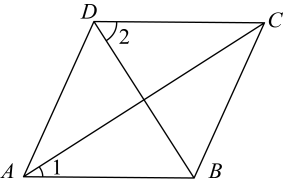 A、 B、 C、 D、6. 如图,在矩形ABCD中,∠BAC=60°,以点A为圆心,任意长为半径作圆弧分别交AB、AC于点M、N,再分别以点M、N为圆心,大于MN的长为半径作弧,两弧交于点P,作射线AP交BC于点E,若BE=1,则△AEC的面积为( )
A、 B、 C、 D、6. 如图,在矩形ABCD中,∠BAC=60°,以点A为圆心,任意长为半径作圆弧分别交AB、AC于点M、N,再分别以点M、N为圆心,大于MN的长为半径作弧,两弧交于点P,作射线AP交BC于点E,若BE=1,则△AEC的面积为( ) A、1 B、2 C、 D、7. 如图, 在矩形 ABCD 中, , 对角线AC与BD相交于点 , A E 垂直平分OB于点 E, 则 BC的长为( )
A、1 B、2 C、 D、7. 如图, 在矩形 ABCD 中, , 对角线AC与BD相交于点 , A E 垂直平分OB于点 E, 则 BC的长为( ) A、 B、 C、4 D、28. 如图,矩形 中,E,F是 上的两个点, , ,垂足分别为G,H,若 , , ,且 ,则 ( )
A、 B、 C、4 D、28. 如图,矩形 中,E,F是 上的两个点, , ,垂足分别为G,H,若 , , ,且 ,则 ( )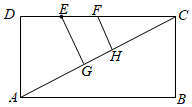 A、 B、 C、3 D、9. 如图,把 剪成三部分,边 , , 放在同一直线 上,点 都落在直线 上,直线 .在 中,若 ,则 的度数为( )
A、 B、 C、3 D、9. 如图,把 剪成三部分,边 , , 放在同一直线 上,点 都落在直线 上,直线 .在 中,若 ,则 的度数为( )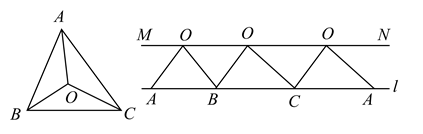 A、 B、 C、 D、10. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
A、 B、 C、 D、10. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )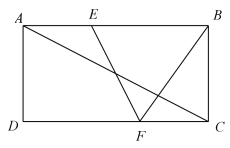 A、 B、 C、4 D、6
A、 B、 C、4 D、6二、填空题
-
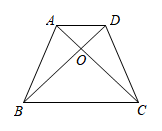
11. 如图所示,已知在梯形ABCD中, , , 则 .
 12. 如图, 中, , , ,D是AB的中点,E是BC的中点, 于点F,则 的长是.
12. 如图, 中, , , ,D是AB的中点,E是BC的中点, 于点F,则 的长是. 13. 正方形和正方形中,点在上, , , 是的中点,那么的长是 .
13. 正方形和正方形中,点在上, , , 是的中点,那么的长是 . 14. 如图,在▱ABCD中,AC是对角线,∠ACD=90°,E 是BC的中点,AF平分∠BAC,连结CF,EF.若CF ⊥AF,AB=5,BC=13,则EF的长为
14. 如图,在▱ABCD中,AC是对角线,∠ACD=90°,E 是BC的中点,AF平分∠BAC,连结CF,EF.若CF ⊥AF,AB=5,BC=13,则EF的长为 15. 正方形ABCD的边长为2,如图1,点E,F均在正方形内部,且BE=EF=FD,∠E=∠F=90°,则BE的长为;如图2,点G,H,I,J,K,L均在正方形内部,且BG=GH=HI=IJ=JK=KL=LD,∠G=∠H=∠I=∠J=∠K=∠L=90°,则BG的长为.
15. 正方形ABCD的边长为2,如图1,点E,F均在正方形内部,且BE=EF=FD,∠E=∠F=90°,则BE的长为;如图2,点G,H,I,J,K,L均在正方形内部,且BG=GH=HI=IJ=JK=KL=LD,∠G=∠H=∠I=∠J=∠K=∠L=90°,则BG的长为.
三、作图题
-
16. 图1,图2都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段AB的端点均在格点上,分别按要求画出图形.
 (1)、在图1中画出等腰三角形ABC,且点C在格点上.(画出一个即可)(2)、在图2中画出以AB为边的菱形ABDE,且点D,E均在格点上.
(1)、在图1中画出等腰三角形ABC,且点C在格点上.(画出一个即可)(2)、在图2中画出以AB为边的菱形ABDE,且点D,E均在格点上.四、解答题
-
17. 如图,在中,E,F是对角线AC上的两点,且 . 求证:AE=CF.
 18. 已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F.
18. 已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F. (1)、求证:四边形AECF是矩形;(2)、当△ABC满足什么条件时,四边形AECF是正方形?
(1)、求证:四边形AECF是矩形;(2)、当△ABC满足什么条件时,四边形AECF是正方形?五、实践探究题
-
19. 【探究与证明】成语“以不变应万变”中蕴含着某种数学原理.
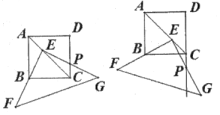
图1 图2
【动手操作】如图1,是正方形的对角线,点E是上的一个动点,过点E和B作等腰直角 , 其中 , , 与射线交于点P.
请完成:
(1)、试判断图1中的和的数量关系;(2)、当点P在线段上时,求证:.(3)、【类比操作】如图2,当点P在线段的延长线上时.是否还成立?请判断并证明你的结论.20. 如图,在△ABC中,AB=AC,点E在AB上,点 F 在 AC 的延长线上,且 BE =CF,连结 EF交 BC 于点D,延长 BC 至点G,使 BD=GD,连结 EG,FG,BF.试探究 CF 和GF之间的数量关系,并说明理由. 21.
21. (1)、【知识呈现】如图①,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.求证:四边形AFCE是菱形;(2)、【知识应用】如图②,直线EF分别交矩形ABCD的边AD、BC于点E、F , 将矩形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为G , 若 , , 则EF的长为;(3)、【知识拓展】如图③,直线EF分别交平行四边形ABCD的边AD、BC于点E、F , 将平行四边形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为G , 若 , , , 则四边形AFCE的面积为.
(1)、【知识呈现】如图①,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.求证:四边形AFCE是菱形;(2)、【知识应用】如图②,直线EF分别交矩形ABCD的边AD、BC于点E、F , 将矩形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为G , 若 , , 则EF的长为;(3)、【知识拓展】如图③,直线EF分别交平行四边形ABCD的边AD、BC于点E、F , 将平行四边形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为G , 若 , , , 则四边形AFCE的面积为.六、综合题
-
22. 已知:四边形是长方形,点 , 分别在边和上, , , ,
 (1)、 , .(2)、设的面积为 , 用含的式子表示S .(3)、在(2)的条件下,当的情况下,动点从出发沿线段运动,速度为每秒个单位长度运动时间为求为何值时的面积与面积相等?
(1)、 , .(2)、设的面积为 , 用含的式子表示S .(3)、在(2)的条件下,当的情况下,动点从出发沿线段运动,速度为每秒个单位长度运动时间为求为何值时的面积与面积相等?
-

