人教版初中数学八年级下学期 第十八章 平行四边形 单元测试 A卷
试卷更新日期:2024-03-19 类型:单元试卷
一、选择题
-
1. 下列命题中,属于假命题的是( )A、菱形的面积等于两条对角线乘积的一半 B、矩形的对角线相等 C、对角线互相垂直的平行四边形是矩形 D、对角线相等的菱形是正方形2. 已知四边形ABCD是菱形,则下列结论中,不一定正确的是( )A、∠A=∠B=∠C=∠D B、AB=BC=CD=DA C、AC⊥BD D、AC平分∠BAD和∠BCD3. 如图,D,E分别是△ABC的边BA,BC的中点.若AC=3,则 DE 的长为 ( )
 A、2 B、 C、3 D、4. 如图,在△ABC中,D是AB 的中点,E,F在AC 上,且AE=EF,BC=CF.若∠A=25°,∠ADE=10°,则∠ABC的度数为 ( )
A、2 B、 C、3 D、4. 如图,在△ABC中,D是AB 的中点,E,F在AC 上,且AE=EF,BC=CF.若∠A=25°,∠ADE=10°,则∠ABC的度数为 ( ) A、35° B、40° C、45° D、50°5. 如图,在▱ABCD 中,AC 与 BD 相交于点O,∠ODA=90°,OA=6,OB=2,则AD的长是( )
A、35° B、40° C、45° D、50°5. 如图,在▱ABCD 中,AC 与 BD 相交于点O,∠ODA=90°,OA=6,OB=2,则AD的长是( )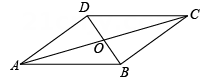 A、6 B、4 C、4 D、46. 如图,在矩形ABCD中,AO=5,CD=6,则AD的长为 ( )
A、6 B、4 C、4 D、46. 如图,在矩形ABCD中,AO=5,CD=6,则AD的长为 ( )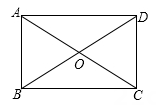 A、5 B、6 C、7 D、87. 已知四边形 ABCD 是平行四边形,有下列条件:①AB=BC;②∠ABC=90°;③∠ABD=∠CBD;④AC⊥BD. 从中选一个条件作为补充,能使□ABCD变为菱形的是 ( )A、① B、①③ C、②④ D、①③④8. 如图,□ABCD的两条对角线相交于点O.若AC=4,BD=5,BC=3,则△BOC的周长为( )
A、5 B、6 C、7 D、87. 已知四边形 ABCD 是平行四边形,有下列条件:①AB=BC;②∠ABC=90°;③∠ABD=∠CBD;④AC⊥BD. 从中选一个条件作为补充,能使□ABCD变为菱形的是 ( )A、① B、①③ C、②④ D、①③④8. 如图,□ABCD的两条对角线相交于点O.若AC=4,BD=5,BC=3,则△BOC的周长为( )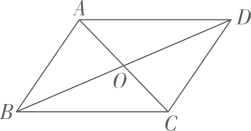 A、6 B、7.5 C、9 D、129. 依据所标数据,下列四边形一定为平行四边形的是( )A、
A、6 B、7.5 C、9 D、129. 依据所标数据,下列四边形一定为平行四边形的是( )A、 B、
B、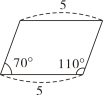 C、
C、 D、
D、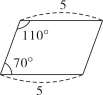 10. 如图,在正方形 ABCD中,E是AC 上的一点,且 AB=AE,则∠EBC的度数为 ( )
10. 如图,在正方形 ABCD中,E是AC 上的一点,且 AB=AE,则∠EBC的度数为 ( ) A、37.5° B、30° C、22.5° D、12.5°
A、37.5° B、30° C、22.5° D、12.5°二、填空题
-
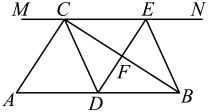
11. 在ABCD中,已知AB=15,AC=13,BC边上的高等于12,则ABCD的周长是 .12. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上, EF⊥AB,OG∥EF,AD=10,EF=4,则BG的长为.
 13. 如图,在矩形 ABCD的边AD 上找一点 P,使点 P 到B,C两点的距离之和最短,则点 P 的位置应该在.
13. 如图,在矩形 ABCD的边AD 上找一点 P,使点 P 到B,C两点的距离之和最短,则点 P 的位置应该在. 14. 如图,在菱形ABCD中,AB=10cm,AC=16cm,E,F分别是CD和BC的中点,连结EP并延长与AB的延长线相交于点G,则EG的长度为cm
14. 如图,在菱形ABCD中,AB=10cm,AC=16cm,E,F分别是CD和BC的中点,连结EP并延长与AB的延长线相交于点G,则EG的长度为cm 15. 如图,在平行四边形中, , 的平分线交于点E,交的延长线于点F,则cm.
15. 如图,在平行四边形中, , 的平分线交于点E,交的延长线于点F,则cm.
三、作图题
-
16. 如图所示为两张大小完全相同的6×6方格纸,每个小方格都是边长为1的正方形,小方格的顶点叫做格点,以格点为顶点的多边形叫做格点多边形.网格中有一个边长为2的格点正方形,按下列要求画出拼图后的格点平行四边形.
 (1)、把图1中的格点正方形分割成两部分,再通过图形变换拼成一个格点平行四边形,在图1中画出这个格点平行四边形.(2)、把图2中的格点正方形分割成三部分,再通过图形变换拼成一个格点平行四边形,在图2中画出这个格点平行四边形.
(1)、把图1中的格点正方形分割成两部分,再通过图形变换拼成一个格点平行四边形,在图1中画出这个格点平行四边形.(2)、把图2中的格点正方形分割成三部分,再通过图形变换拼成一个格点平行四边形,在图2中画出这个格点平行四边形.四、解答题
-
17. 如图,在ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上, 且AE=CF.
 (1)、求证:四边形EGFH是平行四边形;(2)、连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.18. 如图,在▱ABCD 中,延长 DA 到点 E,延长BC到点 F,使得 AE=CF,连结 EF,分别交AB,CD于点M,N,连结 DM,BN.求证:
(1)、求证:四边形EGFH是平行四边形;(2)、连结BD交AC于点O,若BD= 10,AE+CF=EF ,求EG的长.18. 如图,在▱ABCD 中,延长 DA 到点 E,延长BC到点 F,使得 AE=CF,连结 EF,分别交AB,CD于点M,N,连结 DM,BN.求证: (1)、△AEM≌△CFN.(2)、四边形 BMDN 是平行四边形.
(1)、△AEM≌△CFN.(2)、四边形 BMDN 是平行四边形.五、实践探究题
-
19. 问题:如图,在ABCD中,AB=8,AD=5,∠DAB,∠ABC的平分线AE ,BF分别与直线CD交于点E,F,求EF的长.
答案:EF=2.
探究:
(1)、把“问题”中的条件“AB= 8”去掉,其余条件不变.①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)、把“问题”中的条件“AB=8 ,AD=5”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求的值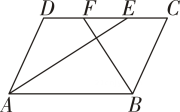 20. 人教版初中数学教科书八年级下册第53页设置了如下一个“思考”栏目:
20. 人教版初中数学教科书八年级下册第53页设置了如下一个“思考”栏目:思考
如图2-3,矩形ABCD的对角线AC,BD相交于点O.我们观察 ,在 中,BO是斜边AC上的中线,BO与AC有什么关系?

经过思考与探究,从而得到了直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半.
现在,我们一起来探究这条性质的证明过程:
如图1:在 中, ,CD是斜边AB上的中线.
求证: .
证明:延长CD至点E,使 ,连接AE,BE.
……
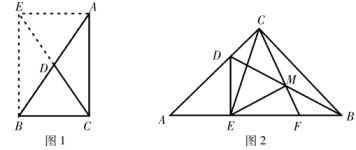
(1)、请你根据以上提示,结合图形,写出完整的证明过程.(2)、定理应用:如图2, 中, ,D为边AC上一点, 于点E,连接BD,M为BD的中点,CM的延长线交AB于点F,连接EC,EM.
①CM与EM的数量关系是 .
②若BD是 的平分线,且 ,则 °.
21. 在数学实践活动课上,“卓越”小组准备研究如下问题:如图,为直尺的一条边,四边形为一正方形纸板、、、均为直角 (1)、【操作发现】
(1)、【操作发现】如图小组成员小方把正方形的一条边与重合放置,刘老师在与同学们交流研讨时又做出了的平分线 , 交正方形的边于点 .
则此时的度数为;与的度数之间的关系为 .
(2)、【问题探究】受小方同学的启发,小组成员小丽将正方形纸板按如图放置,若此时记的度数为 , 其他条件不变,请帮小丽同学探究:与的度数之间的关系是否发生改变,并说明理由.
(3)、【拓展延伸】组内其他同学也都继续探索,将正方形按如图放置,刘老师同样做出了的平分线 , 请直接写出与的度数之间的关系.
六、综合题
-
22. 如图,在菱形中,对角线 , 交于点 , 过点作的垂线,垂足为点 , 延长到点 , 使 , 连接 .
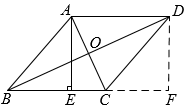 (1)、求证:四边形是矩形;(2)、若 , , 求的长.
(1)、求证:四边形是矩形;(2)、若 , , 求的长.
-