2023-2024学年初中数学人教版七年级下学期 第九章 不等式与不等式组 单元测试 B卷
试卷更新日期:2024-03-19 类型:单元试卷
一、选择题
-
1. 不等式组 的解集在数轴上表示为 ( )A、
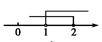 B、
B、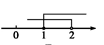 C、
C、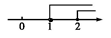 D、
D、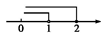 2. 已知关于x的不等式(a﹣1)x>2的解集为 , 则a的取值范围是( )A、a<1 B、a>1 C、a<0 D、a>03. 若 , 则下列各式正确的是( )A、2a<2b B、 C、 D、-a<-b4. 若关于x的不等式(1-m)x≤1-m的解集为x>1,则m的值可以取( )A、-1 B、0 C、1 D、25. 若 , 则 由小到大排列正确的是 ( )A、 B、 C、 D、6. 若不等式组有解,则的取值范围是( )A、 B、 C、 D、7. 不等式的非负整数解有( )A、1个 B、2个 C、3个 D、4个8. 若关于x的不等式组恰好有3个整数解,且关于y的方程的解是非负数,则符合条件的所有整数m之和是( )A、-6 B、-5 C、-3 D、-29. 八年级某小组同学去植树,若每人平均植树7棵,则还剩9棵,若每人平均植树9棵,则有1位同学有植树但植树棵数不到3棵.则同学人数为( )A、8人 B、9人 C、10人 D、11人10. 对非负实数x“四舍五入”到个位的值记为 , 即当n为非负整数时,若 , 则 . 反之,当n为非负整数时,若 , 则 . 例如: , . 给出下列说法:
2. 已知关于x的不等式(a﹣1)x>2的解集为 , 则a的取值范围是( )A、a<1 B、a>1 C、a<0 D、a>03. 若 , 则下列各式正确的是( )A、2a<2b B、 C、 D、-a<-b4. 若关于x的不等式(1-m)x≤1-m的解集为x>1,则m的值可以取( )A、-1 B、0 C、1 D、25. 若 , 则 由小到大排列正确的是 ( )A、 B、 C、 D、6. 若不等式组有解,则的取值范围是( )A、 B、 C、 D、7. 不等式的非负整数解有( )A、1个 B、2个 C、3个 D、4个8. 若关于x的不等式组恰好有3个整数解,且关于y的方程的解是非负数,则符合条件的所有整数m之和是( )A、-6 B、-5 C、-3 D、-29. 八年级某小组同学去植树,若每人平均植树7棵,则还剩9棵,若每人平均植树9棵,则有1位同学有植树但植树棵数不到3棵.则同学人数为( )A、8人 B、9人 C、10人 D、11人10. 对非负实数x“四舍五入”到个位的值记为 , 即当n为非负整数时,若 , 则 . 反之,当n为非负整数时,若 , 则 . 例如: , . 给出下列说法:①;
②;
③当 , m为非负整数时,有;
④若 , 则非负实数x的取值范围为;
⑤满足的所有非负实数x的值有4个.
以上说法中正确的个数为( )
A、1 B、2 C、3 D、4二、填空题
-
11. 举例说明“若是有理数,则”是错误的,请写出一个的值: .12. 某业主贷款22000元购进一台机器,生产某种产品.已知产品的成本每个5元,售价是每个8元.若每月能生产、销售2000个产品,问至少个月后能赚回这台机器的贷款.13. 已知非负实数满足条件 , , 设的最大值为 , 最小值为 , 则的值为.14. 小明沿着某公园的环形跑道(周长大于)按逆时针方向跑步,并用跑步软件记录运动轨迹,他从起点出发,每跑 , 软件会在运动轨迹上标注出相应的里程数.前的记录数据如图所示,当小明跑了2圈时,他的运动里程数(填“”“=”或“”);如果小明跑到时恰好回到起点,那么此时小明总共跑的圈数为 .
 15. 如果关于的不等式组仅有五个整数解为 , , , , , 若在第四象限,那么满足上述条件的整数 , 组成的点的坐标共有个.
15. 如果关于的不等式组仅有五个整数解为 , , , , , 若在第四象限,那么满足上述条件的整数 , 组成的点的坐标共有个.三、计算题
-
16. 解下列不等式(组):(1)、(2)、(3)、
四、解答题
-
17. 解不等式组 , 并将解集在数轴上表示出来.
 18. 一家游泳馆每年6到8月出售夏季会员证,每张会员证80元,只限本人使用,凭证购入场券每张1元,不凭证购入场券每张3元.(1)、什么情况下,购会员证与不购证付一样的钱?(2)、什么情况下,购会员证比不购证更合算?(3)、什么情况下,不购会员证比购证更合算?
18. 一家游泳馆每年6到8月出售夏季会员证,每张会员证80元,只限本人使用,凭证购入场券每张1元,不凭证购入场券每张3元.(1)、什么情况下,购会员证与不购证付一样的钱?(2)、什么情况下,购会员证比不购证更合算?(3)、什么情况下,不购会员证比购证更合算?五、实践探究题
-
19. 下面是张莉同学解不等式的过程,请认真阅读并完成相应任务.
解不等式: .
去分母,得24-(x-7)>8x+4.
(1)、任务一:“去分母”这一步的变形依据是____(填“A”或“B”).A、不等式两边乘(或除以)同一个正数,不等号的方向不变. B、不等式两边乘(或除以)同一个负数,不等号的方向改变.(2)、任务二:请完成上述解不等式的余下步骤,并把解集表示在数轴上.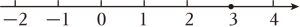 20. 阅读与思考
20. 阅读与思考阅读以下例题:
解不等式: .
解:①当时,即 , 原不等式可化为一元一次不等式 ,
解这个不等式,得 . .
②当时,即 ,
原不等式可化为一元一次不等式 , 解这个不等式,得 , (依据)
.
③当时,即时,原不等式可化为 , 不成立,此时不等式无解.
所以不等式的解为或 .
任务:
(1)、填空:上述解答过程中的“依据”是指 .(2)、仿照例题利用分类讨论思想解不等式: .21. 阅读下列材料:已知 , 且 , , 试确定的取值范围.
解: , ,
, .
又 ,
①.
同理得②.
由①②,得 ,
.
请按照上述方法,解答下列问题.
若 , 且方程的解适合不等式 , , 求的取值范围,并写出的最大值和最小值
六、综合题
-
22. 对于不等式:(且),当时,;当时, , 请根据以上信息,解答以下问题:(1)、解关于x的不等式:;(2)、若关于x的不等式: , 其解集中无正整数解,求k的取值范围;(3)、若关于x的不等式: , 当且时,在上总存在x的值使得其成立,求k的取值范围.23. 学校购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需要26元;3只A型节能灯和2只B型节能灯共需要29元;(1)、求1只A型和1只B型节能灯的售价各是多少元?(2)、学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯的数量的3倍,不少于B型节能灯数量的2倍,有几种购买方案,哪种方案最省钱?
-