2023-2024学年初中数学人教版七年级下学期 第九章 不等式与不等式组 单元测试 A卷
试卷更新日期:2024-03-19 类型:单元试卷
一、选择题
-
1. 一个不等式的解表示在数轴上如图所示,则这个不等式可以是( )
 A、 B、 C、 D、2. 不等式组中的两个不等式的解集在同一个数轴上表示正确的是( )A、
A、 B、 C、 D、2. 不等式组中的两个不等式的解集在同一个数轴上表示正确的是( )A、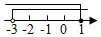 B、
B、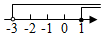 C、
C、 D、
D、 3. 若 , 且 , 当时,关于x的代数式恰好能取到两个非负整数值,则a的取值范围是( )A、 B、 C、 D、4. 不等式的正整数解有( )A、1个 B、2个 C、3个 D、4个5. 下列不等式变形正确的是( )A、由a>b , 得ac>bc B、由a>b , 得a﹣2<b﹣2 C、由ab>ac , 得b>c D、由 , 得b>c6. 已知电灯电路两端的电压U为220V,通过灯泡的电流强度I(A)的最大限度不得超过0.11A.设选用灯泡的电阻为R(Ω),下列说法正确的是( )A、R至少2000Ω B、R至多2000Ω C、R至少24.2Ω D、R至多24.2Ω7. 2023年9月23日,第19届亚运会将在我国杭州市举办.为此,某校举行了关于杭州亚运会的知识竞赛.现共有30道选择题,答对一题得10分,若答错或不答一道题,则扣3分.要使总得分不少于70分则应该至少答对几道题?若设答对x题,则根据题意可列不等式为( )A、 B、 C、 D、8. 估算的值是在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间9. 如果不等式组的解为 , 那么的取值范围是( )A、 B、 C、 D、10. 某业主贷款2.2万元购进一台机器,生产某种产品.已知产品的成本是每个5元,售价是每个8元,应付的税款和其他费用是售价的10%,若每个月能生产、销售2000个产品,问至少几个月后能赚回这台机器的贷款?( )A、4 B、5 C、6 D、7
3. 若 , 且 , 当时,关于x的代数式恰好能取到两个非负整数值,则a的取值范围是( )A、 B、 C、 D、4. 不等式的正整数解有( )A、1个 B、2个 C、3个 D、4个5. 下列不等式变形正确的是( )A、由a>b , 得ac>bc B、由a>b , 得a﹣2<b﹣2 C、由ab>ac , 得b>c D、由 , 得b>c6. 已知电灯电路两端的电压U为220V,通过灯泡的电流强度I(A)的最大限度不得超过0.11A.设选用灯泡的电阻为R(Ω),下列说法正确的是( )A、R至少2000Ω B、R至多2000Ω C、R至少24.2Ω D、R至多24.2Ω7. 2023年9月23日,第19届亚运会将在我国杭州市举办.为此,某校举行了关于杭州亚运会的知识竞赛.现共有30道选择题,答对一题得10分,若答错或不答一道题,则扣3分.要使总得分不少于70分则应该至少答对几道题?若设答对x题,则根据题意可列不等式为( )A、 B、 C、 D、8. 估算的值是在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间9. 如果不等式组的解为 , 那么的取值范围是( )A、 B、 C、 D、10. 某业主贷款2.2万元购进一台机器,生产某种产品.已知产品的成本是每个5元,售价是每个8元,应付的税款和其他费用是售价的10%,若每个月能生产、销售2000个产品,问至少几个月后能赚回这台机器的贷款?( )A、4 B、5 C、6 D、7二、填空题
-
11. 不等式组的解是 .12. 疫情期间,有一批患者要入住邵阳市中心医院的某栋大楼,若每间住4人,则有38人无法入住;若每间住5人,则最后一间没住满.若设房间数为x间,则可列不等式组为: .13. 已知不等式组的解集中共有3个整数,则的取值范围是: .14. 已知不等式组无解,则m的取值范围是 .15. 如果一个数表中某一列各数之和为负数,那么改变该列中所有数的符号,称之为一次“操作”,下表是由8个整数组成的数表,若经过一次“操作”后,使可使新的数表每行的各数之和与每列的各数之和均为非负数,则整数a的值为 .
a
a2﹣1
﹣a
﹣a2
2﹣a
1﹣a2
a﹣2
a2
三、计算题
-
16. 解不等式(组)(1)、(2)、
四、解答题
-
17. 解不等式组
下面是某同学的部分解答过程,请认真阅读并完成任务:
解:解不等式①,得 第1步
合并同类项,得 第2步
两边都除以 , 得 第3步
任务一:该同学的解答过程中第 ▲ 步出现了错误,这一步的依据是 ▲ , 不等式①的正确解是 ▲ .
任务二:解不等式②,并写出该不等式组的解集.
18. 解不等式组:并把不等式组的解集在数轴上表示出来.
五、实践探究题
-
19.(1)、解不等式组:(2)、下面是小彬同学解二元一次方程组的过程,请认真阅读并完成相应任务.
解方程组:
解: , 得 , ………………第一步
, 得 ………………第二步
所以 ………………第三步
把代入得 ………………第四步
所以原方程组的解为 ………………第五步
任务一:上述解二元一次方程组的方法叫做 ▲ 法;以上求解步骤中,第一步的依据是 ▲ ;
任务二:第 ▲ 步开始出现错误,具体错误是 ▲ ;
任务三:直接写出该方程组正确的解.
20. 课堂上,老师设计了“接力游戏”,规则:一列同学每人只完成解不等式的一步变形,即前一个同学完成一步,后一个同学接着前一个同学的步骤进行下一步变形,直至解出不等式的解集.请根据下面的“接力游戏”回答问题.(1)、任务一:①在“接力游戏”中,乙同学是根据进行变形的.A.等式的基本性质
B.不等式的基本性质
C.乘法对加法的分配律
②在“接力游戏”中,出现错误的是同学,这一步错误的原因是 .
(2)、任务二:在“接力游戏”中该不等式的正确解集是 .(3)、任务三:除纠正上述错误外,请你根据平时的学习经验,针对解不等式时还需要注意的事项给同学们提一条建议.接力游戏
老师
甲同学
乙同学
丙同学
丁同学
戊同学
21. 阅读以下例题:解不等式: .解:当 , 则 ,
即可以写成: , 解不等式组得: .
.
当若 , 则 ,
即可以写成: , 解不等式组得: .
.
综合以上两种情况:原不等式的解集为:或 .
以上解法的依据为:当 , 则同号.
请你模仿例题的解法,解不等式:
(1)、;(2)、 .六、综合题
-
22. 为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买 个甲种文具、 个乙种文具共需花费 元;购买 个甲种文具、 个乙种文具共需花费 元.(1)、求购买一个甲种文具、一个乙种文具各需多少元?(2)、若学校计划购买这两种文具共 个,投入资金不少于 元又不多于 元,设购买甲种文具 个,求有多少种购买方案?(3)、设学校投入资金 元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?23. 樱桃是一种常见水果,其中含有丰富的维生素、铁元素、蛋白质、胡萝卜素等营养成分具有补血、抗氧化、健脾益肾的作用,深受人们的喜爱.某水果批发商从水果批发市场批发樱桃进行零售,批发价格与零售价格如下表:
樱桃品种
红灯樱桃
大紫樱桃
批发价(元/kg)
30
50
零售价(元/kg)
55
80
请解答下列问题:
(1)、第一天,该经营户批发红灯樱桃和大紫樱桃共用去了10000元,这两种樱桃当天全部销售完一共能赚多少元钱?(2)、第二天,该经营户仍用10000元批发这两种樱桃,要想当天全部售完后所赚钱不少于8100元,则该经营户最少应批发红灯樱桃多少?
-