2023-2024学年初中数学人教版七年级下学期 第七章 平面直角坐标系 单元测试 B卷

试卷更新日期：2024-03-19 类型：单元试卷

进入 出卷网 下载

一、选择题

  • 1. 下列五个命题：

    ①如果两个数的绝对值相等，那么这两个数的平方相等；②内错角相等；③在同一平面内，垂直于同一条直线的两条直线互相平行；④两个无理数的和一定是无理数；⑤坐标平面内的点与有序数对是一一对应的.其中真命题的个数是（    ）

    A、2个 B、3个 C、4个 D、5个

    查看试题解析

  • 2. 点P（m+3，m﹣2）在直角坐标系的x轴上，则点P的坐标为（   ）
    A、（0，5） B、（5，0） C、（﹣5，0） D、（0，﹣5）

    查看试题解析

  • 3. 若点P（x，y）在第四象限，且|x|＝2，|y|＝3，则x+y＝（　　）
    A、﹣1 B、1 C、5 D、﹣5

    查看试题解析

  • 4. 点C在x轴的上方，y轴的左侧，距离x轴3个单位长度，距离y轴5个单位长度，则点C的坐标为（    ）
    A、(−3 ， 5) B、(3 ， −5) C、(5 ， −3) D、(−5 ， 3)

    查看试题解析

  • 5. 在平面直角坐标系xOy中，点P(1−m ， 8)在第二象限，则m的取值范围是（ ）
    A、m>1 B、m<1 C、m≤1 D、m≥1

    查看试题解析

  • 6. 在平面直角坐标系中，将A(1 ， m2) ， 沿着y轴的负方向向下平移2m2+3个单位后得到B点．有四个点M(1 ， −m2−4) ， N(1 ， −2m2−3) ， P(1 ， −m2) ， Q(1 ， −3m2)一定在线段AB上的是（ ）
    A、点M B、点N C、点P D、点O

    查看试题解析

  • 7. 如图，在象棋盘上建立直角坐标系，使“将”位于(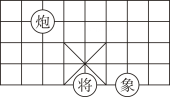0 ， 0) ， “象”位于(2 ， 0) ， 则“炮”位于（ ）

    A、(3 ， −2) B、(4 ， −2) C、(−2 ， 4) D、(−2 ， 3)

    查看试题解析

  • 8. 某电影院里3排4号可以用数对(3 ， 4)表示，小明买了7排2号的电影票，用数对可表示为（ ）
    A、(2 ， 7) B、(7 ， 2) C、(3 ， 4) D、(4 ， 3)

    查看试题解析

  • 9. 如图，在方格纸中，点P ， M的坐标分别记为(−1 ， 0) ， (0 ， 2) ． 若MN∥PQ ， 则点N的坐标可能是（    ）

      

    A、(1 ， 1) B、(2 ， 1) C、(3 ， 0) D、(4 ， −1)

    查看试题解析

  • 10. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第一次从原点O运动到点P1(1 ， 1) ， 第二次从点P1运动到点P2(2 ， 0) ， 第三次从点P2运动到点P3(3 ， −2) ， …，按这样的运动规律，第2023次从点P2022运动到点P2023后，此时点P2023的坐标是（ ）

    A、(2023 ， 1) B、(2023 ， 2) C、(2023 ， −2) D、(2023 ， 0)

    查看试题解析

二、填空题

  • 11. 如果把2街5巷记为(2 ， 5) ， 那么4街3巷可以表示为 ．

    查看试题解析

  • 12. 在平面直角坐标系中，已知线段AB∥x轴，且AB=5 ， 点A的坐标是(−2 ， 4) ， 则点B的坐标为 ．

    查看试题解析

  • 13. 若点A （2   ，  3m−1）在x轴上，点B （2 n+1  ，  3）在y轴上，则代数式6m+4n的值是 ．

    查看试题解析

  • 14. 已知点A(4，-3)，B(x，-3)，若AB∥x轴，且线段AB的长为5，则x= ．

    查看试题解析

  • 15. 如图，在平面直角坐标系上有个点P(1，0)，点P第1次向上跳动1个单位至点P1(1，1)，紧接着第2次向左跳动2个单位至点P2(―1，1)，第3次向上跳动1个单位，第4次向右跳动3个单位，第5次又向上跳动1个单位，第6次向左跳动4个单位，……，依此规律跳动下去，点P第100次跳动至点P100的坐标是 ．

    查看试题解析

三、解答题

  • 16. 在平面直角坐标系中，已知点M(m−2 ， 2m−7) ， 点N(n ， 3) ， 若MN∥y轴，且MN=2 ， 求n的值．

    查看试题解析

  • 17. 在平面直角坐标系中，已知点M(2−m ， 1+2m) ．
    (1)、若点M在y轴上，求M点的坐标；
    (2)、若点M在第二、四象限的角平分线上，求M点的坐标．

    查看试题解析

  • 18. 已知点P(2a-1，3-a)，且点P在第二象限．
    (1)、求a的取值范围．
    (2)、若点P到坐标轴的距离相等，求点P的坐标．

    查看试题解析

四、实践探究题

  • 19. 问题情境：

    在平面直角坐标系xOy中有不重合的两点A（x1 ， y1）和点B（x2 ， y2），小明在学习中发现，若x1=x2 ， 则AB∥y轴，且线段AB的长度为|y1﹣y2|；若y1=y2 ， 则AB∥x轴，且线段AB的长度为|x1﹣x2|；

    （应用）：

    (1)、若点A（﹣1，1）、B（2，1），则AB∥x轴，AB的长度为 ．
    (2)、若点C（1，0），且CD∥y轴，且CD=2，则点D的坐标为 ．
    (3)、（拓展）：

    我们规定：平面直角坐标系中任意不重合的两点M（x1 ， y1），N（x2 ， y2）之间的折线距离为d（M，N）=|x1﹣x2|+|y1﹣y2|；例如：图1中，点M（﹣1，1）与点N（1，﹣2）之间的折线距离为d（M，N）=|﹣1﹣1|+|1﹣（﹣2）|=2+3=5．

    解决下列问题：

    已知E（2，0），若F（﹣1，﹣2），求d（E，F）；

    (4)、如图2，已知E（2，0），H（1，t），若d（E，H）=3，求t的值；
    (5)、如图3，已知P（3，3），点Q在x轴上，且三角形OPQ的面积为3，求d（P，Q）．

    查看试题解析

五、综合题

  • 20. 在直角坐标系中，已知点P（2m+4，m-1）
    (1)、若点P的纵坐标比横坐标大3 ，则点P的坐标为；
    (2)、若点P到两坐标轴的距离相等 ，则点P的坐标为；
    (3)、若点P在过点A(2，-5) ，且与x轴平行的直线上，求点P的坐标。

    查看试题解析

  • 21. 在平面直角坐标系xOy中，我们把横、纵坐标都是整数的点叫做整点．已知点A(6 ， 2) ， B(m ， 34) ， C(m ， 5) ， 其中m为正整数，且A，B，C三点不在同一直线上，分别连接AB ， BC ， CA ， 设这三条线段围成的区域内部（不包括线段AB ， AC ， BC上的点）的整点个数为n．

    (1)、当m=8时，直接写出整点个数n，并写出这些整点的坐标；
    (2)、若n=3 ， 则m的值为；
    (3)、若n=0 ， 则m的值为 ．

    查看试题解析

  • 22. 对于平面直角坐标中的任意两点P，Q，若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和，则称P，Q两点为“和合点”，如图1中的P，Q两点即为“和合点”．

    (1)、已知点A(−4 ， 8) ， B(6 ， 0) ， C(6 ， 6) ， D(−2 ， 9) ．

    ①在上面四点中，与点E(−5 ， −7)为“和合点”的是      ▲      ；

    ②若点F(−3 ， 0) ， 过点F作直线l⊥x轴，点G直线l上，A、G两点为“和合点”，则点G的坐标为      ▲      ；

    ③若点M(2a ， 3b)在第二象限，点N(−3a ， −b)在第四象限，且A、M两点为“和合点”，D、N两点为“和合点”，求a，b的值．

    (2)、如图2，已知点H(−5 ， 0) ， K(0 ， 5) ， 点R(x ， y)是线段HK上的一动点，且满足x−y=−5 ， 过点T(n ， 0)作直线m⊥x轴，若在直线m上存在点S，使得R，S两点为“和合点”，直接写出n的取值范围．

    查看试题解析