2023-2024学年初中数学人教版七年级下学期 第七章 平面直角坐标系 单元测试 A卷

试卷更新日期：2024-03-19 类型：单元试卷

进入 出卷网 下载

一、选择题

  • 1. 在平面直角坐标系中，点P（﹣5，0）在（   ）

    A、第二象限 B、x轴上 C、第四象限 D、y轴上

    查看试题解析

  • 2. 在平面直角坐标系中，已知 A(−2 ， −3) ，则点 A 到 y 轴的距离为（   ）
    A、-2 B、2 C、3 D、13

    查看试题解析

  • 3. 如果 ab<0 ，那么点P (a ， b) 所在象限为（    ）
    A、第二象限 B、第四象限 C、第一或第三象限 D、第二或第四象限

    查看试题解析

  • 4. 已知点Q的坐标为 (2 ， −3) ，点P的坐标为 (2a+2 ， a−5) ，若直线 PQ⊥y 轴，则点P的坐标为（ ） 
    A、(2 ， −5) B、(2 ， 2) C、(6 ， −3) D、(−14 ， −3)

    查看试题解析

  • 5. 已知点M(3 ， 4) ， 若直线MN与x轴平行，则N点坐标可能是（ ）
    A、(3 ， 5) B、(4 ， 5) C、(5 ， 3) D、(5 ， 4)

    查看试题解析

  • 6. 某气象台为了预报台风，首先需要确定台风中心的位置，则下列说法能确定台风中心位置的是（ ）
    A、北纬38° B、距气象台500海里 C、北纬21.5° ， 东经109° D、北海市附近

    查看试题解析

  • 7. 在平面直角坐标系中，点A的坐标为(−1 ， 3) ， 点B的坐标为(5 ， 3) ， 则线段AB上任意一点的坐标可表示为（ ）

    A、(3 ， x)(−1<x≤5) B、(x ， 3)(−1≤x≤5) C、(3 ， x)(−5≤x≤1) D、(x ， 3)(−5≤x≤1)

    查看试题解析

  • 8. 某学校的平面示意图如图所示，如果医院所在位置的坐标为(−1 ， 0) ， 则(1 ， 2)所在的位置是（ ）

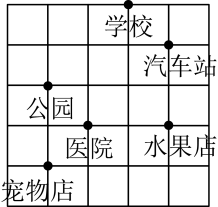    A、医院 B、学校 C、汽车站 D、水果店

    查看试题解析

  • 9. 如图，小手盖住的点的坐标可能是（　　）．

    A、（﹣3，4）； B、（5，2） C、（﹣3，﹣6）； D、（6，﹣4）．

    查看试题解析

  • 10. 如果点P(x ， y)的坐标满足x+y=xy ， 那么称点P为“美丽点”，若某个“美丽点”P到y轴的距离为2 ， 则点P的坐标为（ ）
    A、(2 ， −2) B、(−2 ， 23) C、(23 ， −2)或(2 ， 2) D、(2 ， 2)或(−2 ， 23)

    查看试题解析

二、填空题

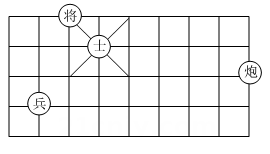
  • 11. 若点P(m−1 ， 2m+4)在x轴上，则m= ．

    查看试题解析

  • 12. 如图所示，若“兵”的位置是(1 ， 1) ， “炮”的位置是(8 ， 2) ， 则“将”的位置可以表示为 ．

    查看试题解析

  • 13. 在平面直角坐标系中，若点M（1，x）与点N（1，3）之间的距离是5，则x的值是 ．

    查看试题解析

  • 14. 已知两点A(a ， 5) ， B(0 ， b)的距离为4，且直线AB∥x轴，则b−a的算术平方根为；

    查看试题解析

  • 15. 在平面直角坐标系中，点A(−5 ， 3)、B(3 ， 3) ， C(4 ， 1) ， 若在平面直角坐标中存在一点D ， 使得AB⊥CD ， 且AB=2CD ， 则点D的坐标为 ．

    查看试题解析

三、解答题

  • 16. 已知在平面直角坐标系中，点A的坐标为(a−3 ， 2a+1) ．
    (1)、若点A在y轴上，求出点A的坐标；
    (2)、若点A到x轴的距离为5 ， 求出点A的坐标．

    查看试题解析

  • 17. 已知点A(3a−9 ， 2a−10) ， 解答下列问题：
    (1)、若点B的坐标为(4 ， 5) ， 且AB//y轴，求a的值；
    (2)、若点A在第四象限，且a是整数，求点A的坐标．

    查看试题解析

  • 18. 已知点A(3a−4 ， a−1) ， 根据条件，求点A的坐标．
    (1)、点A的横坐标是纵坐标的2倍．
    (2)、点A在过点P(5 ， −2)且与y轴平行的直线上．

    查看试题解析

四、实践探究题

  • 19. 综合与实践：
    (1)、问题背景：

    已知A(1 ， 2) ， B(3 ， 0) ， C(1 ， −1) ， D(−3 ， −3) ． 在平面直角坐标系中描出这几个点，并分别找到线段AB和CD中点P1、P2 ， 然后写出它们的坐标，则P1    ▲         ， P2    ▲         ．

    (2)、探究发现：

    结合上述计算结果，你能发现若线段的两个端点的坐标分别为(x1 ， y1) ， (x2 ， y2) ， 则线段的中点坐标为 ．

    (3)、拓展应用：

    利用上述规律解决下列问题：已知三点E(−1 ， 2) ， F(3 ， 1) ， G(1 ， 4) ， 第四个点H(x ， y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合，求点H的坐标．

    查看试题解析

  • 20.  老师布置了一项编题作业给小亮，小颖和小明的学习小组：结合图象创设情景，加入适当的条件，设计一道数学问题，并作出合理的解释。以下是老师参与下的学习小组活动片段.

    [观察图象]

    如图，是老师在平面直角坐标系中画出的图象，请同学们结合图象创设背景。

     [创设背景]

    小颖说：可以创设这样的背影：一辆货车从甲地行驶到乙地去拉货，到达乙地后旋即返回，这里横坐标表示行驶的时间，单位是小时，纵坐标表示货车与甲地的距离，单位是千米。

    小亮说：显然去时的速度快于返回的速度，可设去乙地的速度为60km/h，返回甲地的速度为30km/h.

    小明说：还应该给出条件，甲、乙两地间的距离为120千米。

    老师说：非常好，这样就可以试着提出问题了。

    [提出问题]

    小颖说：可以求货车从甲地去乙地的时间是多少。

    小亮说：可以问A、B两地的坐标是多少。

    小明说：可以问货车何时距离甲地30km。

    老师说：大家的想法真好，就按大家的设计，下面可以概括出题了。

    请结合以上对话，回答问题：

    (1)、货车从甲地去乙地时间为h.
    (2)、请求出图中A、B两点的坐标.
    (3)、当货车距离甲地30km时，行驶的时间是多少？

    查看试题解析

  • 21. 阅读材料回答问题

    在平面直角坐标系中，定义，点P沿着水平和竖直方向运动到达点Q的最短路径的长度为P ， Q两点之间的“横纵距离”.如图所示，点A的坐标为(2 ， 3) ， 则A ， O两点的“横纵距离”为5．

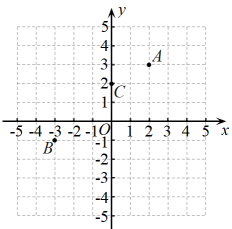
    解决问题

    (1)、已知点B的坐标为(−3 ， −1) ， 则B ， O两点的“横纵距离”为；A ， B两点的“横纵距离”为；
    (2)、已知点C的坐标为(0 ， 2) ， 写出两个与点C的“横纵距离”为3的点的坐标．
    (3)、拓展延伸
    已知D ， O两点的“横纵距离”为5；D ， C两点的“横纵距离”为3.请写出满足条件的点D的纵坐标的取值范围．

    查看试题解析

五、综合题

  • 22. 如图，这是某校的平面示意图，如以正东为x轴正方向，正北为y轴正方向建立平面直角坐标系后，得到初中楼的坐标是(−4 ， 2) ， 实验楼的坐标是(−4 ， 0) ．

    (1)、坐标原点应为的位置．
    (2)、在图中画出此平面直角坐标系；
    (3)、校门在第象限；图书馆的坐标是；分布在第一象限的是 ．

    查看试题解析

  • 23. 已知点A(−2 ， 0)､B(0 ， 4)､C(m+2 ， m−1)

    (1)、当点C在y轴上时，求点C坐标及△ABC的面积；
    (2)、当BC∥x轴时：

    ①求B､C两点之间的距离；

    ②直接比较S△BCA      ▲            S△BCO（填“>”或“<”或“=”）

    (3)、点C(m+2 ， m−1)不可能在第象限．

    查看试题解析