2024年河北省初中毕业生升学文化课模拟考试数学试卷(三)(包含所有课标新增内容)
试卷更新日期:2024-03-18 类型:中考模拟
一、选择题
-
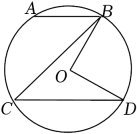
1. 下列语句正确的是( )A、“米”表示向东走米 B、表示没有温度 C、可以表示正数 D、既是正数也是负数2. 某种新冠病毒毒株的直径大约为0.000000093米,这个数用科学记数法可以表示为( )A、 B、 C、 D、3. 估计的值应在( )A、7和8之间 B、8和9之间 C、9和10之间 D、10和11之间4. 如图,在⊙O中,弦AB∥CD , 若∠BOD=82°,则∠ABC的度数为( )
 A、41° B、55° C、66° D、88°5. 如图,长方形中, , , 在数轴上,若以点为圆心,的长为半径作弧交数轴于点 , 则点表示的数为
A、41° B、55° C、66° D、88°5. 如图,长方形中, , , 在数轴上,若以点为圆心,的长为半径作弧交数轴于点 , 则点表示的数为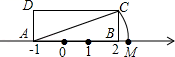 A、 B、 C、2 D、6. 阳阳同学在复习老师已经批阅的作业本时,发现有一道填空题破了一个洞(如图),则破损部分的式子可能是( )
A、 B、 C、2 D、6. 阳阳同学在复习老师已经批阅的作业本时,发现有一道填空题破了一个洞(如图),则破损部分的式子可能是( )化简:
A、 B、 C、 D、7. 如图,将直角三角形ABC沿AB方向平移2cm得到 , DF交BC于点H , , , 则阴影部分的面积为( )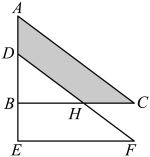 A、6cm2 B、8cm2 C、12cm2 D、16cm28. 下列说法正确的个数是( )
A、6cm2 B、8cm2 C、12cm2 D、16cm28. 下列说法正确的个数是( )①数轴上的点与有理数是——对应的;
②的倒数是;
③是最简二次根式;
④一个实数不是正实数就是负实数;
⑤绝对值小于的整数共有5个.
A、1个 B、2个 C、3个 D、4个9. 某工厂用如图①所示的长方形和正方形纸板制作如图②所示的A、B两种长方体形状的无盖纸盒.现有正方形纸板120张,长方形纸板360张,刚好全部用完,则下列结论中正确的个数是 ( )①甲同学:设制作A型盒个数为x,根据题意可得4x+3×=360;②乙同学:设制作B型盒用正方形纸板的张数为m,根据题意可得3×+4(120-m)=360;③制作A型盒72个;④制作B型盒需正方形纸板共48张.
 A、1 B、2 C、3 D、410. 如图是测量一颗玻璃球体积的过程:(1)将300ml的水倒进一个容量为500ml的杯子中;(2)将四颗相同的玻璃球放入水中,结果水没有满;(3)再加一颗同样的玻璃球放入水中,结果水满溢出.
A、1 B、2 C、3 D、410. 如图是测量一颗玻璃球体积的过程:(1)将300ml的水倒进一个容量为500ml的杯子中;(2)将四颗相同的玻璃球放入水中,结果水没有满;(3)再加一颗同样的玻璃球放入水中,结果水满溢出.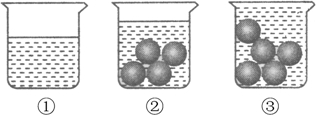
根据以上过程,推测这样一颗玻璃球的体积在( )
A、20cm3以上,30cm3以下 B、30cm3以上,40cm3以下 C、40cm3以上,50cm3以下 D、50cm3以上,60cm3以下11. 如图,二次函数的图象与x轴的一个交点为 , 对称轴是直线 , 下列结论正确的是( )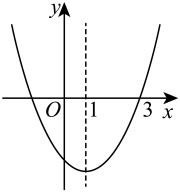 A、 B、 C、 D、点在函数图象上12. 如图,的内切圆与 , , 分别相切于点 , , , 若的半径为 , , 则的值和的大小分别为( )
A、 B、 C、 D、点在函数图象上12. 如图,的内切圆与 , , 分别相切于点 , , , 若的半径为 , , 则的值和的大小分别为( )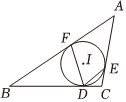 A、 , B、 , C、 , D、 ,13. 某综合实践活动小组设计了简易电子体重秤: 制作一个装有踏板(踏板质量忽略不计)的可变电阻 (如图 1), 当人站上踏板时, 通过电压表显示的读数 换算为人的质量 ), 已知 随着 的变化而变化 (如图 2), 与踏板上人的质量 的关系见图3. 则下列说法不正确的是 ( )
A、 , B、 , C、 , D、 ,13. 某综合实践活动小组设计了简易电子体重秤: 制作一个装有踏板(踏板质量忽略不计)的可变电阻 (如图 1), 当人站上踏板时, 通过电压表显示的读数 换算为人的质量 ), 已知 随着 的变化而变化 (如图 2), 与踏板上人的质量 的关系见图3. 则下列说法不正确的是 ( )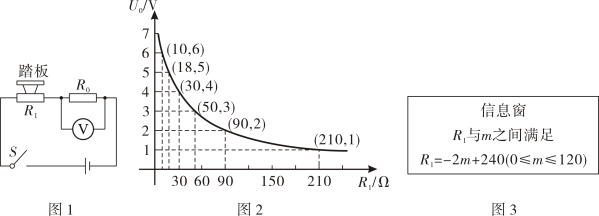 A、在一定范围内, 越大, 越小 B、当 时, 的阻值为 C、当踏板上人的质量为 时, D、若电压表量程为 , 为保护电压表, 该电子体重科可称的最大质量是14. 如图,为驾驶员的盲区,驾驶员的眼睛点处与地面 的距离为米,车头近似看成一个矩形,且满足 , 若盲区的长度是米, 则车宽的长度为( )米.
A、在一定范围内, 越大, 越小 B、当 时, 的阻值为 C、当踏板上人的质量为 时, D、若电压表量程为 , 为保护电压表, 该电子体重科可称的最大质量是14. 如图,为驾驶员的盲区,驾驶员的眼睛点处与地面 的距离为米,车头近似看成一个矩形,且满足 , 若盲区的长度是米, 则车宽的长度为( )米. A、 B、 C、 D、15. 天干地支纪年法源于中国,是上古文明的产物,又称节气历或中国阳历,有十天干与十二地支,如表:
A、 B、 C、 D、15. 天干地支纪年法源于中国,是上古文明的产物,又称节气历或中国阳历,有十天干与十二地支,如表:天干
甲
乙
丙
丁
戊
己
庚
辛
壬
癸
4
5
6
7
8
9
0
1
2
3
地支
子
丑
寅
卯
辰
已
午
未
申
酉
戌
亥
4
5
6
7
8
9
10
11
12
1
2
3
算法如下:先用年份的尾数查出天干,再用年份除以12的余数查出地支.如2014年,尾数4为甲,2014除以12余数为10,10为午,那么2014年就是甲午年.则2023年是( )
A、甲卯年 B、甲寅年 C、癸卯年 D、癸寅年16. 如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
①BF=CF; ②若BE⊥AC,则CF=DF;
③连结EF,若BE⊥AC,则∠DFE=2∠ABE
④.若BE平分∠ABC,则FG=;
 A、①②③ B、③④ C、①②④ D、①②③④
A、①②③ B、③④ C、①②④ D、①②③④二、填空题
-
17. 阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.

小云的作法如下:
①在直线l上任取两点B,C;
②以A为圆心,以BC长为半径作弧;以C为圆心,以AB长为半径作弧,两弧相交于点D;
③作直线AD.
直线AD即为所求.

老师说:“小云的作法正确.”请回答:小云的作图依据是 .
18. 有一种手持烟花,该烟花有10个花弹,每1秒发一发花弹,每一发花弹的飞行路径均相同.第一发花弹的飞行高度(米)与飞行时间(秒)满足关系式:.当秒时,该花弹的高度为米.(1)、第一发花弹的飞行高度的最大高度是米.(2)、第一发花弹飞行过程中与其他花弹同一高度时,其的值为.19. 如图,在Rt△ABC中,∠CAB=90°,I为△ABC的内心,延长CI交AB于点D.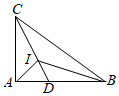 (1)、∠BIC=°;(2)、若BD=3,BI=4,则AB= .
(1)、∠BIC=°;(2)、若BD=3,BI=4,则AB= .三、解答题
-
20. 已知代数式A=6x2+3xy+2y , B=3x2﹣2xy+5x .(1)、求A﹣2B;(2)、当 , y=﹣6时,求A﹣2B的值;(3)、若A﹣2B的值与x的取值无关,求y的值.21. 有4张背面完全相同的纸牌A,B,C,D,其中正面分别画有如图所示4个不同的几何图形,小华将这4张纸牌背面朝上洗匀后摸出1张,放回洗匀后再摸1张.
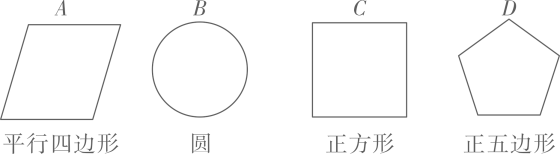 (1)、用画树状图或列表的方法表示两次摸牌所有可能出现的结果.(纸牌可用A,B,C,D表示)(2)、求摸出的两张纸牌正面所画的几何图形,既是轴对称图形又是中心对称图形的概率.22. 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了 5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
(1)、用画树状图或列表的方法表示两次摸牌所有可能出现的结果.(纸牌可用A,B,C,D表示)(2)、求摸出的两张纸牌正面所画的几何图形,既是轴对称图形又是中心对称图形的概率.22. 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了 5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).甲、乙两人射箭成绩统计表
第1次
第2次
第3次
第4次
第5次
甲
9
4
7
4
6
乙
7
5
7
a
7
小宇的作业:
解
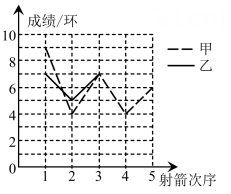 (1)、a= , x₂= , 甲成绩的众数是 , 乙成绩的中位数是(2)、请完成图中表示乙成绩变化情况的折线.(3)、①请求出乙成绩的方差,并比较谁的成绩比较稳定.
(1)、a= , x₂= , 甲成绩的众数是 , 乙成绩的中位数是(2)、请完成图中表示乙成绩变化情况的折线.(3)、①请求出乙成绩的方差,并比较谁的成绩比较稳定.②请你从平均数和方差的角度分析,谁将被选中.
甲、乙两人射箭成绩折线统计图
23. 已知关于x的二次函数 .(1)、求该抛物线的对称轴(用含t的式子表示);(2)、若点 , 在抛物线上,则mn;(填“>”,“<”或“=”)(3)、 , 是抛物线上的任意两个点,若对于且 , 都有 , 求t的取值范围.24. 如图,某公路上有一隧道,顶部是圆弧形拱顶,圆心为O , 隧道的水平宽AB为24m , AB离地面的高度AE=10m , 拱顶最高处C离地面的高度CD为18m.若在拱顶的M , N处安装照明灯,且M , N离地面的高度相等,都为17m.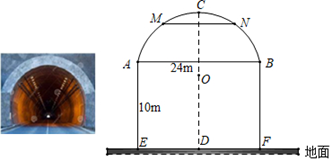 (1)、求圆弧形拱顶的半径的长度.(2)、求MN的长度.25. 在公主岭南站的公主故里广场,有一尊标志性的大清固伦和敬公主雕像,某“数学综合与实践”小组通过实地测量(如示意图)和查阅资料,得到了以下信息:
(1)、求圆弧形拱顶的半径的长度.(2)、求MN的长度.25. 在公主岭南站的公主故里广场,有一尊标志性的大清固伦和敬公主雕像,某“数学综合与实践”小组通过实地测量(如示意图)和查阅资料,得到了以下信息:信息一:雕塑底座高为米.
信息二:在P处用测角仪测得雕像最高点仰角为 , 雕塑底座最高点的仰角为 .
信息三:点在垂直地面的同一条直线上.
信息四:参考数据 , .
请根据以上信息,求公主雕像的高度(精确到米).
 26. 如图,在中, , , , 点D是上一动点(不与点B , C重合), , .
26. 如图,在中, , , , 点D是上一动点(不与点B , C重合), , .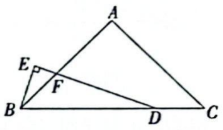 (1)、求的度数;(2)、在点D运动过程中,的值是否为定值?请说明理由;(3)、当时,连接 , 三边上分别有动点P , M , N(点P在上),当的周长取最小值时,求的长.
(1)、求的度数;(2)、在点D运动过程中,的值是否为定值?请说明理由;(3)、当时,连接 , 三边上分别有动点P , M , N(点P在上),当的周长取最小值时,求的长.