2024年河北省初中毕业生升学文化课模拟考试数学试卷(二)
试卷更新日期:2024-03-18 类型:中考模拟
一、选择题
-
1. 要使算式(-1)□3的运算结果最大,则“□”内应填入的运算符号为( )A、+ B、- C、× D、÷2. 有理数a,b在数轴上的对应点的位置如图所示,下列结论中不正确的是( )
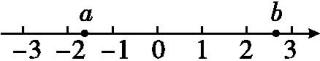 A、a-b<0 B、|a|<|b| C、a+b>0 D、ab>03. 如图,正五边形中,F为边中点,连接 , 则的度数是( )
A、a-b<0 B、|a|<|b| C、a+b>0 D、ab>03. 如图,正五边形中,F为边中点,连接 , 则的度数是( )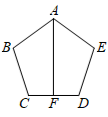 A、 B、 C、 D、4. 如果长方形的长为(4a2-2a+1),宽为(2a+1),则这个长方形的面积为( )A、8a3-4a2+2a-1 B、8a3+4a2-2a-1 C、8a3-1 D、8a3+15. 一次数学活动中,小明对纸带沿AB折叠,量得 , 则的度数为( )
A、 B、 C、 D、4. 如果长方形的长为(4a2-2a+1),宽为(2a+1),则这个长方形的面积为( )A、8a3-4a2+2a-1 B、8a3+4a2-2a-1 C、8a3-1 D、8a3+15. 一次数学活动中,小明对纸带沿AB折叠,量得 , 则的度数为( )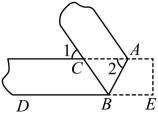 A、 B、 C、 D、6. 据报道,2023年“十一”假期全国国内旅游出游合计7.54亿人次,7.54亿用科学记数法表示是( )A、 B、 C、 D、7. 如图的立体图形由相同大小的正方体积木堆叠而成.判断拿走图中的哪一个积木后,此图形前视图的形状会改变( )
A、 B、 C、 D、6. 据报道,2023年“十一”假期全国国内旅游出游合计7.54亿人次,7.54亿用科学记数法表示是( )A、 B、 C、 D、7. 如图的立体图形由相同大小的正方体积木堆叠而成.判断拿走图中的哪一个积木后,此图形前视图的形状会改变( ) A、甲 B、乙 C、丙 D、丁8. 在中, , 是的中点,求证: .
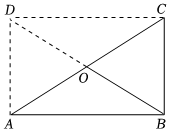
A、甲 B、乙 C、丙 D、丁8. 在中, , 是的中点,求证: .证明:如图,延长至点 , 使 , 连接 , .
……
,
.
下面是“……”部分被打乱顺序的证明过程:①∴四边形是平行四边形;②∵;③∵ , ;④∴四边形是矩形.
A、③①②④ B、③②①④ C、②③①④ D、②①③④9.有一种足球是由32块黑白相间的牛皮缝制而成的(如图),黑皮可看作正五边形,白皮可看作正六边形.设白皮有x块,则黑皮有(32﹣x)块,要求出黑皮、白皮的块数,列出的方程是( )
 A、3x=32﹣x B、3x=5(32﹣x) C、5x=3(32﹣x ) D、6x=32﹣x10. 为响应“双减”政策,进一步落实“立德树人、五育并举”的思想主张,深圳某学校积极推进学生综合素质评价改革,小芳在本学期德、智、体、美、劳的评价得分如图所示,其各项的得分分别为9,8,10,8,7,则该同学这五项评价得分的众数,中位数,平均数分别为( )
A、3x=32﹣x B、3x=5(32﹣x) C、5x=3(32﹣x ) D、6x=32﹣x10. 为响应“双减”政策,进一步落实“立德树人、五育并举”的思想主张,深圳某学校积极推进学生综合素质评价改革,小芳在本学期德、智、体、美、劳的评价得分如图所示,其各项的得分分别为9,8,10,8,7,则该同学这五项评价得分的众数,中位数,平均数分别为( )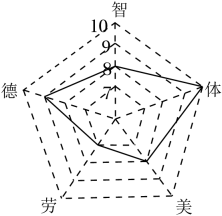 A、8,8,8 B、7,8,7.8 C、8,8,8.7 D、8,8,8.411. 如图,已知钝角 ,依下列步骤尺规作图,并保留了作图痕迹.
A、8,8,8 B、7,8,7.8 C、8,8,8.7 D、8,8,8.411. 如图,已知钝角 ,依下列步骤尺规作图,并保留了作图痕迹.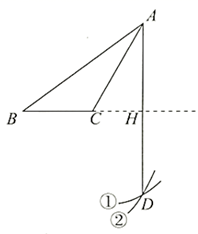
步骤1:以 为圆心, 长为半径画弧①;
步骤2:以 为圆心, 长为半径画弧②,交弧①于点 ;
步骤3:连接 ,交 的延长线于点 .
则下列说法错误的是( )
A、 是 中 边上的高 B、 C、 平分 D、作图依据是:①两点确定一条直线;②到线段两端点距离相等的点在线段的垂直平分线上12. 对于抛物线 , y与x的部分对应值如下表所示:x
…
0
3
4
…
y
…
10
3
…
下列说法中正确的是( )
A、开口向下 B、当时,y随x的增大而增大 C、对称轴为直线 D、函数的最小值是13. 《四元玉鉴》是一部成就辉煌的数学名著,是宋元数学集大成者,也是我国古代水平最高的一部数学著作.该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽”.大意是:现请人代买一批椽,这批椽的总售价为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设6210元购买椽的数量为x株,则符合题意的方程是( )A、 B、 C、 D、14. 已知一次函数的图象与的图象交于点 . 则对于不等式 , 下列说法正确的是( )A、当时, B、当时, C、当且时, D、当且时,15. 如图,在平面直角坐标系中,A(0,3)、B(3,0),以点B为圆心、2为半径的⊙B上有一动点P.连接AP,若点C为AP的中点,连接OC,则OC的最小值为( )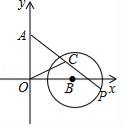 A、1 B、2﹣1 C、 D、﹣116. 如图1,菱形纸片ABCD的边长为2,∠ABC=60°,如图2,翻折∠ABC , ∠ADC , 使两个角的顶点重合于对角线BD上一点P , EF , GH分别是折痕.设BE=x(0<x<2),给出下列判断:
A、1 B、2﹣1 C、 D、﹣116. 如图1,菱形纸片ABCD的边长为2,∠ABC=60°,如图2,翻折∠ABC , ∠ADC , 使两个角的顶点重合于对角线BD上一点P , EF , GH分别是折痕.设BE=x(0<x<2),给出下列判断: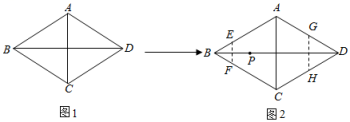
①当x=1时,DP的长为;②EF+GH的值随x的变化而变化;③六边形AEFCHG面积的最大值是;④六边形AEFCHG周长的值不变.
其中正确的是( )
A、①② B、①④ C、②③④ D、①③④二、填空题
-
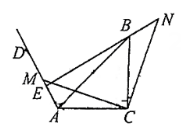
17. 已知a , b互为相反数,c , d互为倒数,m的绝对值是2,则= .18. 如图,现有一矩形纸片为姖形的对角线, , 点为上一点,沿线段将折叠为 , 折痕交于点 , 连接 , 作点关于直线对称的点 , 点恰好落在对角线上,连接 .
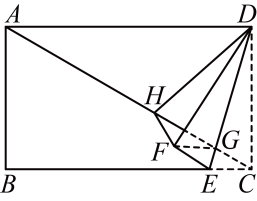 (1)、的大小为;(2)、的长为 .19. 如图1,在中, , 动点从点出发,以每秒1个单位的速度沿线段运动到点停止,同时动点从点出发,以每秒4个单位的速度沿折线运动到点停止.图2是点运动时,的面积与运动时间函数关系的图象,则的值是 .
(1)、的大小为;(2)、的长为 .19. 如图1,在中, , 动点从点出发,以每秒1个单位的速度沿线段运动到点停止,同时动点从点出发,以每秒4个单位的速度沿折线运动到点停止.图2是点运动时,的面积与运动时间函数关系的图象,则的值是 .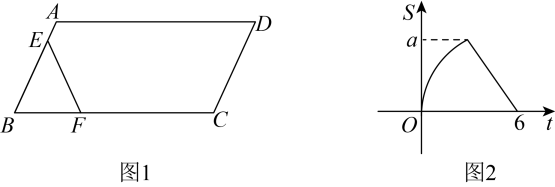
三、解答题
-
20. 聪聪根据市自来水公司的居民用水收费标准,制定了如下水费计算程序转换机示意图:
 (1)、根据该程序转换机计算表中a、b的值;(2)、当时,月应缴纳水费(元)用x的代数式表示为 ▲ ;
(1)、根据该程序转换机计算表中a、b的值;(2)、当时,月应缴纳水费(元)用x的代数式表示为 ▲ ;用户
张大爷
刘奶奶
王阿姨
聪聪家
用户
输入()
8
15
18
25
输入()
输出(元)
24
a
60
b
输出(元)
(3)、小丽家比小明家用水量多 , 水费多44元,则小丽家该月用水多少?21. 阅读下面的图示,并按要求解决问题: 22. 教育部办公厅印发了《关于加强中小学生手机管理的工作通知》,要求中小学生原则上不得将个人手机带入校园,确有需求的,须经家长同意、书面提出申请,进校后应将手机由学校统一保管,禁止带入课堂.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图(1),图(2)所示的统计图,已知“查资料”的人数是48人.
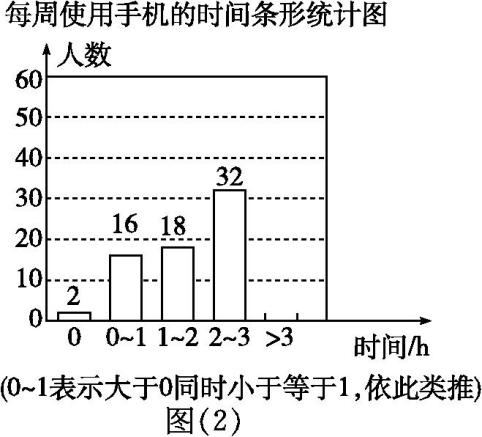
22. 教育部办公厅印发了《关于加强中小学生手机管理的工作通知》,要求中小学生原则上不得将个人手机带入校园,确有需求的,须经家长同意、书面提出申请,进校后应将手机由学校统一保管,禁止带入课堂.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图(1),图(2)所示的统计图,已知“查资料”的人数是48人.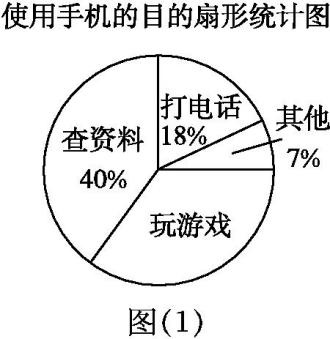
解答下列问题:
(1)、在扇形统计图中,表示“玩游戏”的扇形圆心角度数为 , 补全条形统计图;(2)、该校共有学生2 100人,估计每周使用手机时间在2 h以上(不含2 h)的人数;(3)、请写出一条学生健康使用手机的建议.23.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.
(1)请分别作出下图中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
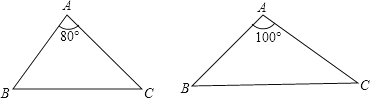
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明).
24. 一名生物学家在研究两种不同的物种A和B在同一生态环境中的资源消耗时发现:50个物种A和100个物种B共消耗了200单位资源;100个物种A和50个物种B共消耗了250单位资源.(1)、求1个物种A和1个物种B各消耗多少单位资源;(2)、已知物种A , B共有200个且A的数量不少于100个.设物种A有a个,物种A , B共消耗的单位资源W .①求W与a的函数关系式;
②当物种A的数量为何值时,物种A、B共消耗的单位资源最少,最小值是多少?

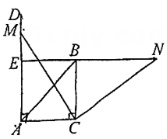 图2
图2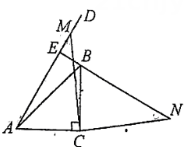 图3
图3