广东省深圳市福田区重点学校2024年直升适应性数学试卷

试卷更新日期：2024-03-18 类型：中考模拟

进入出卷网下载

一、数学选择题（本大题共5小题，每小题3分，共15分，每小题有四个选项，其中只有一项是正确的）

1. 实数﹣2的相反数是（）

A、﹣2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 已知a＝ $\sqrt{5}$ ， b＝2，c＝ $\sqrt{3}$ ，则a、b、c的大小关系是（）

A、b＞a＞c B、a＞c＞b C、a＞b＞c D、b＞c＞a

查看试题解析
3. 函数y＝ $\frac{1}{x^{2}}$ 的大致图象是（）

A、 B、 C、 D、

查看试题解析
4. 小明同学利用计算机软件绘制函数y＝ $\frac{a x}{{(x + b)}^{2}}$ （a、b为常数）的图象如图所示，由学习函数的经验，可以推断常数a、b的值满足（）

A、a＞0，b＞0 B、a＞0，b＜0 C、a＜0，b＞0 D、a＜0，b＜0

查看试题解析
5. 如图，点P是函数y＝ $\frac{k_{1}}{x}$ （k₁＞0，x＞0）的图象上一点，过点P分别作x轴和y轴的垂线，垂足分别为点A、B，交函数y＝ $\frac{k_{2}}{x}$ （k₂＞0，x＞0）的图象于点C、D，连接OC、OD、CD、AB，其中k₁＞k₂ ．下列结论：①CD∥AB；②S_△OCD＝ $\frac{k_{1} - k_{2}}{2}$ ；③S_△DCP＝ $\frac{{(k_{1} - k_{2})}^{2}}{2 k_{1}}$ ，其中正确的是（）

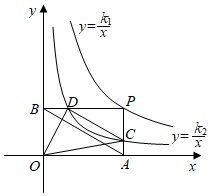A、①② B、①③ C、②③ D、①

查看试题解析

二、数学填空题（本大题共5小题，每小题3分，共15分）

6. 用半径为 $24 c m$ ，面积为 $120 π c m^{2}$ 的扇形纸片，围成一个圆锥的侧面，则这个圆锥的底面圆的半径为 $c m$ ．

查看试题解析
7. 在△ABC中，∠C＝90°，a、b、c分别为∠A、∠B、∠C的对边，若b²＝ac，则sinA的值为．

查看试题解析
8. 平面上5个圆最多能把平面分成个部分．

查看试题解析
9. 如图，四边形ABCD中，已知AC⊥BC，AD⊥BD，垂足分别为C，D．若BC＝2，CD＝3 $\sqrt{2}$ ， ∠ACD＝45°，则AB＝．

查看试题解析
10. 如图，已知平面直角坐标系xOy中，点A的坐标为（3，3），点D的坐标是（6，0），点B是x轴上一动点，过点A作AC⊥AB，垂足为A，且AC•AB＝6．当点B从坐标原点O起沿x轴向右运动到终点D时，点C运动的路径的长度是．

查看试题解析

三、解答题（本大题共4小题，共30分）

11. 计算： $| - \sqrt{3} | - 2 s i n 60 ° + (\frac{1}{4})^{- 1} + (2023 - π)^{0}$ ．

查看试题解析
12. 【问题情境】
在综合实践活动课上，李老师让同桌两位同学用相同的两块含30°的三角板开展数学探究活动，两块三角板分别记作△ADB和△A^'D^'C，∠ADB＝∠A^'D^'C＝90°，∠B＝∠C＝30°，设AB＝2．
【操作探究】
如图1，先将△ADB和△A^'D^'C的边AD、A^'D^'重合，再将△A^'D^'C绕着点A按顺时针方向旋转，旋转角为α（0°≤α≤360°），旋转过程中△ADB保持不动，连接BC．

(1)、当α＝60°时，BC＝；当BC＝2 $\sqrt{2}$ 时，α＝°；

(2)、当α＝90°时，画出图形，并求两块三角板重叠部分图形的面积；

(3)、如图2，取BC的中点F，将△A^'D^'C^'绕着点A旋转一周，点F的运动路径长为．

查看试题解析
13. 如图，已知点A（1，2）、B（5，n）（n＞0），点P为线段AB上的一个动点，反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过点P．小明说：“点P从点A运动至点B的过程中，k值逐渐增大，当点P在点A位置时k值最小，在点B位置时k值最大．”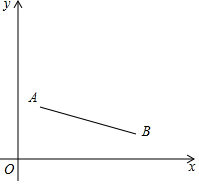

(1)、当n＝1时．
①求线段AB所在直线的函数表达式．
②你完全同意小明的说法吗？若完全同意，请说明理由；若不完全同意，也请说明理由，并求出正确的k的最小值和最大值．

(2)、若小明的说法完全正确，求n的取值范围．

查看试题解析
14. 定义：对角线互相垂直且相等的四边形叫做垂等四边形．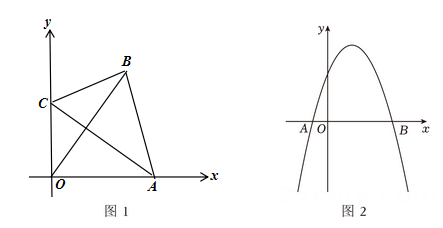

(1)、理解应用：如图，在平面直角坐标系xOy中，已知四边形OABC是垂等四边形，点A的坐标为（4，0），点C的坐标为（0，3），则点B的坐标为．

(2)、综合探究：如图，已知抛物线y＝﹣x²+2x+3与x轴交于A，B两点，点A在点B的左侧，C，D两点在该抛物线上．若以A，B，C，D为顶点的四边形是垂等四边形．设点C的横坐标为m，点D的横坐标为n，且m＞n，求m的值．

查看试题解析