人教版2024年小升初专项复习——圆柱与圆锥
试卷更新日期:2024-03-18 类型:一轮复习
一、单选题
-
1. 把一个圆柱的侧面展开,不可能得到下面的图形是( )A、
 B、
B、 C、
C、 D、
D、
-
2. 下面第( )个图形是圆柱的展开图.A、
 B、
B、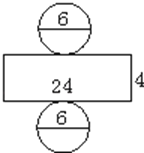 C、
C、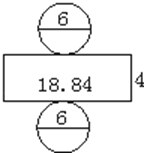 D、
D、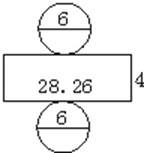
-
3. 把一个棱长为6分米的正方体削成一个最大的圆柱,这个圆柱的体积是( )。A、216立方分米 B、169.56立方分米 C、75.36立方分米
-
4. 圆锥的底面半径扩大两倍,高也扩大两倍,则圆锥体积( )A、扩大4倍 B、扩大6倍 C、扩大8倍
-
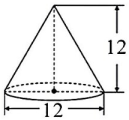
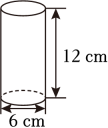
5. 一个高是12cm的圆锥形容器盛满水,将水倒入和它等底的圆柱形量杯里,水的高度是( )cm。A、4 B、12 C、36
-
6. 一个圆柱,挖去一个最大的圆锥,成为一个容器,这个容器的体积是原来圆柱体积( )。A、 B、 C、3倍 D、
-
7. 关于下面圆柱和圆锥的体积,下列说法错误的是( )。(单位:cm)
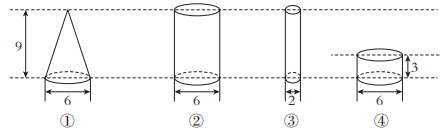 A、①和④的体积相等 B、②的体积是①的 3 倍 C、②的体积是④的 3 倍 D、①和③的体积相等
A、①和④的体积相等 B、②的体积是①的 3 倍 C、②的体积是④的 3 倍 D、①和③的体积相等 -
8. 把一个高为6.28厘米的圆柱体的侧面沿一条高剪开,展开后得到一个正方形,那么原来这个圆柱体的体积约是( )立方厘米A、6.28 B、19.72 C、78.88
-
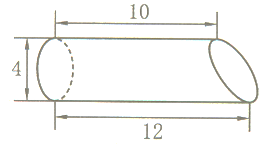
9. 如图,有一根圆柱形木料,沿底面直径纵向切开,下面说法正确的是( )
 A、表面积不变 B、总体积减少 C、表面积增加72cm² D、表面积增加144cm²
A、表面积不变 B、总体积减少 C、表面积增加72cm² D、表面积增加144cm² -
10. 一个长方体、一个圆柱和一个圆锥底面积相等,高也相等。下面说法正确的是( )。A、圆柱的体积比长方体的体积小一些 B、圆锥的体积是长方体体积的 C、圆柱的体积和圆锥的体积相等 D、圆锥的体积最大
二、填空题
-
11. 一个圆锥的底面直径是4厘米,高是3厘米。它的体积是立方厘米。
-
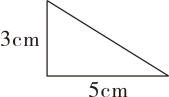
12. 如图,一个直角三角形两条直角边是3厘米和5厘米,任意选一条直角边为轴旋转一周,所形成的图形是 , 体积最大是立方厘米。
-
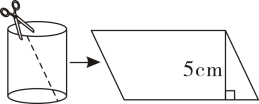
13. 一个圆柱形食品罐(如图),沿着虚线把侧面商标纸剪开,展开后得到一个面积为31.4cm²的平行四边形,那么这个食品罐的体积是cm3。
-
14. 把一个圆柱形木头削成一个最大的圆锥,要削去24立方分米,削成圆锥的体积是立方分米。
-
15. 一个圆柱和一个圆锥等底等高,体积之和是48立方分米,圆锥的体积是 立方分米。
-
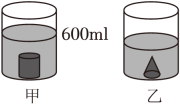
16. 两个大小相同的量杯中,都盛有450mL的水。将等底等高的圆柱形零件与圆锥形零件分别放入两个量杯中,甲水面的刻度如图所示,则乙水面的刻度应显示 mL。
-
17. 做一个底面直径是10厘米、长2米的圆柱形通风管,至少需铁皮平方厘米。
-
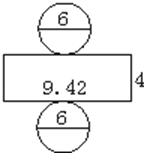
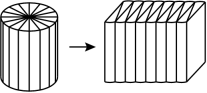
18. 如图,把圆柱体平均分成若干份,再拼成一个近似的长方体。已知长方体的长是12.56cm,高是4cm,这个圆柱体的侧面积是 cm2 , 拼成的长方体表面积比圆柱体多 cm2。
-
19. 一个高5厘米的圆柱体,沿底面直径将圆柱体锯成两块,其表面积增加40平方厘米,原来这个圆柱体的体积是立方厘米。
-
20. 一个装有水的长方体容器长13cm,宽10cm,把一个圆柱和一个圆锥都放入容器中,水面上升了2cm。已知圆柱和圆锥等底等高,圆锥完全浸入水中,圆柱有的高露出水面,则圆柱的体积是cm3。
三、计算题
四、解答题
-
24. 一个圆锥形麦堆,底面积是3.14m2 , 高是1.5m,按每立方米小麦的质量为700kg计,这堆小麦的质量有多少千克?
-
25. 把一个直径是12cm、高是2dm的圆柱形钢件熔铸成一个高是9dm的圆锥形钢件。这个圆锥形钢件的底面积是多少?
-
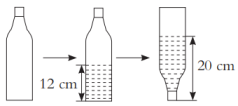
26. 为了测量一个空瓶子的容积,典典进行了如下实验。
①测量出整个瓶子的高度是 30 cm;
②测量出瓶身圆柱部分的内直径是 8 cm;
③给瓶子里注入一些水,把瓶子正放时,测量出水的高度是12 cm;
④把瓶盖拧紧后倒置,此时水的高度是 20 cm。
 (1)、要算出这个瓶子的容积,需要知道。(填序号)(2)、请根据选出的信息,求出这个瓶子的容积。
(1)、要算出这个瓶子的容积,需要知道。(填序号)(2)、请根据选出的信息,求出这个瓶子的容积。 -
27. 如图:有三个高度相等的容器(尺寸见图,单位:cm),如果将乙、丙容器注满水一起倒入甲容器中,那么甲容器水深为多少厘米?

-
28. 一堆9.8方的沙子装入一个高1.8米的圆柱形容器里,露出的部分是一个高0.9米的圆锥形沙堆,这个露出圆锥形沙堆的体积是多少立方米?(1方等于1立方米)

-
29. 在一个棱长20cm的正方体中间挖一个圆柱形孔(如图),圆孔的直径为8cm 。求正方体挖孔后的表面积。