【培优卷】2024年浙教版数学七年级下册3.5整式的化简同步练习

试卷更新日期：2024-03-17 类型：同步测试

进入出卷网下载

一、选择题

1. 已知 $a + \frac{1}{a}$ = $\sqrt{10}$ ，则 $a - \frac{1}{a}$ 的值为（　　）

A、 $\pm 2 \sqrt{2}$ B、8 C、 $\pm \sqrt{6}$ D、6

查看试题解析
2. 如果 $m^{2} + m = 3$ ，那么代数式 $m (m - 2) + (m + 2)^{2}$ 的值为（）

A、14 B、10 C、7 D、6

查看试题解析
3. 若 $A ＝ x^{2} + 2 x - 6 y$ ， $B ＝ - y^{2} + 4 x - 11$ ，则A、B的大小关系为（）

A、A＞B B、A＜B C、A≥B D、A＝B

查看试题解析
4. 已知 $x + y = 6, x - y = 5$ ，则下列计算正确的是（）

A、 ${(x + y)}^{2} = - 36$ B、 ${(y - x)}^{2} = - 10$ C、 $x y = 2.75$ D、 $x^{2} - y^{2} = 25$

查看试题解析
5. 如图，有A，B，C三种不同型号的卡片，每种各10张.A型卡片是边长为a的正方形，B型卡片是相邻两边长分别为a、b的长方形，C型卡片是边长为b的正方形.从中取出若干张卡片（每种卡片至少一张），把取出的这些卡片拼成一个正方形，所有符合要求的正方形的个数是（）

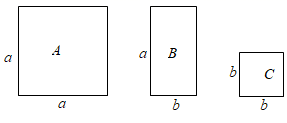A、4 B、5 C、6 D、7

查看试题解析
6. 如图，阴影部分是边长是 $a$ 的大正方形剪去一个边长是 $b$ 的小正方形后所得到的图形，将阴影部分通过割、拼形成新的图形，能够验证的公式为（）

A、 $a^{2} + 2 a b + b^{2} = {(a + b)}^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
7. 在多项式 $16 x^{2} + 1$ 添加一个单项式，使得到的多项式能运用完全平方公式分解因式，则下列表述正确的是（）
嘉琪：添加 $\pm 8 x$ ， $16 x^{2} + 1 \pm 8 x = {(4 x \pm 1)}^{2}$
陌陌：添加 $64 x^{4}$ ， $64 x^{4} + 16 x^{2} + 1 = {(8 x^{2} + 1)}^{2}$
嘟嘟：添加 $- 1$ ， $16 x^{2} + 1 - 1 = 16 x^{2} = {(4 x)}^{2}$

A、嘉琪和陌陌的做法正确 B、嘉琪和嘟嘟的做法正确 C、陌陌和嘟嘟的做法正确 D、三位同学的做法都错误

查看试题解析
8. 如图，用1块边长为a的大正方形，4块边长为b的小正方形和4块长为a，宽为b的长方形 $(a > b)$ ，密铺成正方形 $A B C D$ ，已知 $a b = 3$ ，正方形 $A B C D$ 的面积为S（）

A、若 $a = 2 b + 1$ ，则 $S = 26$ B、若 $a = 2 b + 2$ ，则 $S = 29$ C、若 $S = 33$ ，则 $a = 2 b + 3$ D、若 $S = 28$ ，则 $a = 2 b + 4$

查看试题解析

二、填空题

9. 若 $(2023 - x) (x - 2021) = - 2022$ ，则 ${(2023 - x)}^{2} + {(x - 2021)}^{2}$ 的值为．

查看试题解析
10. 已知 $N = (2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) (2^{16} + 1)$ ，则 $N$ 的个位数字是．

查看试题解析
11. 如图，将一张长方形纸板按图中虚线裁剪成九块，其中有两块边长都为m的大正方形，两块边长都为n的小正方形，五块长为m，宽为n的小长方形．若每块小长方形的面积为7，四块正方形的面积和为100，则这个长方形纸板的周长为．

查看试题解析
12.
如图是我国古代数学家杨辉最早发现的，称为“杨辉三角”．“杨辉三角”中有许多规律，如它的每一行的数字正好对应了（a+b）ⁿ（n为非负整数）的展开式中a按次数从大到小排列的项的系数．例如，（a+b）²=a²+2ab+b²展开式中的系数1、2、1恰好对应图中第三行的数字．请认真观察此图，写出（a+b）³的展开式（a+b）³= ．

查看试题解析

三、解答题

13. 如图，现有一块长为 $(3 a + b)$ 米，宽为 $(a + b)$ 米的长方形地块，规划将阴影部分进行绿化，中间预留部分是边长为 $(2 a - b)$ 米的正方形．

(1)、求绿化的面积S（用含a，b的代数式表示，并化简）；

(2)、若 $a = 3$ ， $b = 2$ ，绿化成本为100元/平方米，则完成绿化共需要多少元？

查看试题解析
14. 【阅读理解】若 $x$ 满足 $(9 - x) (x - 4) = 4$ ，求 ${(9 - x)}^{2} + {(x - 4)}^{2}$ 的值．
解：设 $9 - x = a$ ， $x - 4 = b$ ，则 $(9 - x) (x - 4) = a b = 4$ ， $a + b = (9 - x) + (x - 4) = 5$ ，

$∴ {(9 - x)}^{2} + {(x - 4)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 5^{2} - 2 \times 4 = 17$ ．

这种方法叫做换元法，利用换元法达到简化方程的目的，体现了转化的数学思想．

请仿照上例解决下面的问题：

(1)、若 $x$ 满足 $(50 - x) (x - 20) = 40$ ，求 ${(50 - x)}^{2} + {(x - 20)}^{2}$ 的值．

(2)、若 $x$ 满足 $(8 - x) (2 - x) = 12$ ，求代数式 ${(10 - 2 x)}^{2}$ 的值．

(3)、已知正方形 $A B C D$ 的边长为 $x$ ， $E$ ， $F$ 分别是 $A D$ 、 $D C$ 上的点，且 $A E = 3$ ， $C F = 5$ ，长方形 $E M F D$ 的面积是48，分别以 $M F$ 、 $D F$ 作正方形，求阴影部分的面积．

查看试题解析
15. 通过构造一个图形，利用两种方法计算该图形的面积，从而得到一个等式，这种方法习惯称为“算两次”，在数学学习中有着广泛的应用．公元三世纪，三国时代的赵爽创制了“勾股圆方图”，验证了著名的勾股定理．

(1)、如图1，边长为 $a$ 的大正方形 $A B C D$ 中有一个边长为 $b$ 的小正方形 $A E F G$ ．请你用两种不同方法求阴影部分的面积；

(2)、如图2，现有若干张 $A$ 型、 $B$ 型、 $C$ 型三种不同形状的纸片，请你利用纸片拼出一个几何图形直观地解释 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ；

(3)、在（1）的条件下，若 $a = 4 c m$ ， $b = 2 c m$ ，一动点 $M$ 以每秒 $1 c m$ 的速度从点 $E$ 出发，沿着 $E \to B \to C \to D \to G$ 方向运动．
①当点 $M$ 在 $E \to B$ 上运动时，请表示出 $△ E F M$ 的面积 $y$ 与 $t$ 的关系式： ▲ ；
②是否存在 $t$ 使得 $△ E F M$ 的面积为 $1 c m^{2}$ ，若存在，求出 $t$ 的值；若不存在，请说明理由．

查看试题解析

【培优卷】2024年浙教版数学七年级下册3.5整式的化简 同步练习

一、选择题

二、填空题

三、解答题

【培优卷】2024年浙教版数学七年级下册3.5整式的化简同步练习