【提高卷】2024年浙教版数学七年级下册3.5整式的化简同步练习

试卷更新日期：2024-03-17 类型：同步测试

进入出卷网下载

一、选择题

1. 计算 $(1 - \frac{1}{2^{2}}) \times (1 - \frac{1}{3^{2}}) \times (1 - \frac{1}{4^{2}}) \times (1 - \frac{1}{5^{2}}) \times (1 - \frac{1}{6^{2}})$ 的值为（）．

A、 $\frac{5}{12}$ B、 $\frac{1}{2}$ C、 $\frac{7}{12}$ D、 $\frac{11}{30}$

查看试题解析
2. 若 $x^{2} + 2 (m - 3) x + 49$ 是一个二项式的平方，则m的值为（）

A、 $- 4$ B、10 C、4或 $- 10$ D、 $- 4$ 或10

查看试题解析
3. 已知 $a^{2} - 25 b^{2} = 4$ ， $a - 5 b = \frac{1}{4}$ ，则 $a + 5 b$ 的值为（）

A、16 B、8 C、4 D、14

查看试题解析
4. 式子 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) \dots (2^{1024} + 1) + 1$ 化简的结果为（）

A、 $2^{1010} + 1$ B、 $2^{1010}$ C、 $2^{2020} + 1$ D、 $2^{2048}$

查看试题解析
5. 已知 ${(2023 - a)}^{2} + {(a - 2022)}^{2} = 7$ ，则代数式 $(2023 - a) (a - 2022)$ 的值是（）

A、2 B、1 C、3 D、 $- 3$

查看试题解析
6. 在下列各式：①a-b＝b-a；②（a-b）²＝（b-a）²；③（a-b）²＝-（b-a）²；④（a-b）³＝（b-a）³； ⑤（a+b）（a-b）＝（-a-b）（-a+b）中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，图1中的阴影部分移动成图2，根据两个图形中阴影部分的关系，可以验证下列哪个计算公式（）

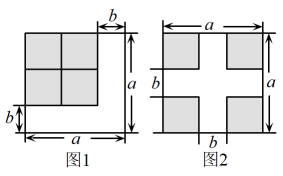A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $(a + b)^{2} = 4 a b + (a - b)^{2}$

查看试题解析
8. 如图4张长为a、宽为b（a＞b）的长方形纸片，按如图的方式拼成一个边长为（a+b）的正方形，图中空白部分的面积为S₁ ，阴影部分的面积为S₂ ．若S₁＝2S₂ ，则a：b=（）

A、3：2 B、5：2 C、2：1 D、3：1

查看试题解析

二、填空题

9. 若 $2^{a} \times 2^{b} = 16 ， a b = 2$ ，则 $(a - b)^{2} =$ .

查看试题解析
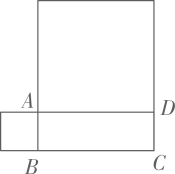
10. 我们学习的平方差公式不但可以使运算简便，也可以解决一些复杂的数学问题.尝试计算（1＋ $\frac{1}{2}$ ）（1＋ $\frac{1}{2^{2}}$ ）（1＋ $\frac{1}{2^{4}}$ ）（1＋ $\frac{1}{2^{8}}$ ）＋ $\frac{1}{2^{15}}$ 的值是.

查看试题解析
11. 如图，长方形 $A B C D$ 的周长为8，分别以长方形的一条长和一条宽向外作两个正方形，且这两个正方形的面积和为10，则长方形 $A B C D$ 的面积是．

查看试题解析
12. 阅读材料解决问题．
小明遇到下面一个问题：
计算：(2+1)(2²+1)(2⁴+1)(2⁸+1)．
经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：
(2+1)(2²+1)(2⁴+1)(2⁸+1)
=(2-1)(2+1)(2²+1)(2⁴+1)(2⁸+1)
=(2²-1)(2²+1)(2⁴+1)(2⁸+1)
=(2⁴-1)(2⁴+1)(8+1)
=(2⁸-1)(2⁸+1)
=2¹⁶-1．
请你仿照小明解决问题的方法，计算：(6+1)(6²+1)(6⁴+1)(6⁸+1)=

查看试题解析

三、解答题

13. 我们知道完全平方公式是 $(a + b)^{2} = a^{2} + 2 a b + b^{2} ， (a - b)^{2} = a^{2} - 2 a b + b^{2}$ ，由此公式我们可以得出以下结论：① $(a - b)^{2} = (a + b)^{2} - 4 a b$ ；② $a b = \frac{1}{2} [(a + b)^{2} - (a^{2} + b^{2})]$ ；利用公式①和②解决下列问题：

(1)、若 $m + n = 10 ， m n = - 3$ ，求 $(m - n)^{2}$ 的值．

(2)、若 $m$ 满足 $(2023 - 2 m)^{2} + (2 m - 2024)^{2} = 7$ ，求 $(2023 - 2 m) (2 m - 2024)$ 的值．

查看试题解析
14. 如图1是一个长为 $4 a$ 、宽为 $b$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）

(1)、观察图2请你写出 ${(a + b)}^{2}$ 、 ${(a - b)}^{2}$ 、 $a b$ 之间的等量关系是；

(2)、根据（1）中的结论，若 $x + y = 5$ ， $x \cdot y = \frac{9}{4}$ ，则 $x - y =$ ；

(3)、拓展应用：若 ${(2019 - m)}^{2} + {(m - 2020)}^{2} = 15$ ，求 $(2019 - m) (m - 2020)$ 的值．

查看试题解析
15. 某中学九年级的学生人数比八年级学生多．做广播操时，九年级排成的是一个规范的长方形方阵，每排 $(3 a + b)$ 人，站有 $(2 a + 2 b)$ 排；八年级站的正方形方阵，排数和每排人数都是 $2 (a + b)$ ，其中 $a > b$ ．

(1)、试求该学校九年级比八年级多多少名学生；用a与b的代数式表示．

(2)、当 $a = 10$ ， $b = 2$ 时，求该学校九年级比八年级多多少名学生．

查看试题解析

【提高卷】2024年浙教版数学七年级下册3.5整式的化简 同步练习

一、选择题

二、填空题

三、解答题

【提高卷】2024年浙教版数学七年级下册3.5整式的化简同步练习