【培优卷】2024年浙教版数学七年级下册3.4乘法公式同步练习

试卷更新日期：2024-03-17 类型：同步测试

进入出卷网下载

一、选择题

1. 设 $a = x - 2017$ ， $b = x - 2019$ ， $c = x - 2018$ ．若 $a^{2} + b^{2} = 34$ ，则 $c^{2}$ 的值是（）

A、16 B、12 C、8 D、4

查看试题解析
2. 不论x，y取什么实数，代数式x²＋y²＋2x－4y＋7的值（）

A、不小于2 B、不小于7 C、为任何实数 D、可能为负数

查看试题解析
3. 计算 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) \cdot \cdot \cdot (2^{64} + 1)$ ，结果是（）

A、 $2^{64} - 1$ B、 $2^{64}$ C、 $2^{32} - 1$ D、 $2^{128} - 1$

查看试题解析
4. 已知： $a (a - 1) - (a^{2} - b) = - 5$ . 求：代数式 $\frac{a^{2} + b^{2}}{2} - a b$ 的值为（）

A、-5 B、5 C、 $\frac{25}{2}$ D、25

查看试题解析
5. 有4张长为 $a$ 、宽为 $b (a > b)$ 的长方形纸片，按如图的方式拼成一个边长为 $(a + b)$ 的正方形，图中阴影部分的面积为 $S_{1}$ ，空白部分的面积为 $S_{2}$ ．若 $S_{1} = \frac{1}{2} S_{2}$ ，则 $a$ 、 $b$ 满足（）

A、 $2 a = 3 b$ B、 $2 a = 5 b$ C、 $a = 2 b$ D、 $a = 3 b$

查看试题解析
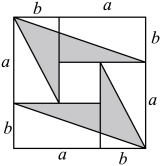6. 比较图1和图2你可以得到 ① ，如图3，点C是线段 $A B$ 上的一点，以 $A C$ ， $C F$ 为边向两边作正方形，设 $A B = 8$ ，两正方形的面积和 $S_{1} + S_{2} = 26$ ，求图中阴影部分的面积是 ② （）

A、① $(a + b)^{2} = (a - b)^{2} + 4 a b$ ②26 B、① $(a + b)^{2} - (a - b)^{2} = + 4 a b$ ② $\frac{19}{2}$ C、① $(a + b) (a - b) = a^{2} - b^{2}$ ② $\frac{19}{2}$ D、① $(a + b)^{2} - (a - b)^{2} = + 4 a b$ ②26

查看试题解析
7. 如图所示，阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后得到的图形，小佳将阴影部分通过拼剪，拼成了图①、图②、图③三种新的图形，其中能够验证平方差公式的是（）．

A、①② B、①③ C、②③ D、①②③

查看试题解析
8. 如图，大正方形的边长为m，小正方形的边长为n，x，y表示四个相同长方形的两边长(x>y) ．则①x-y=n；②xy= $\frac{m^{2} - n^{2}}{4}$ ；③x²-y²=mn；④x²+y²= $\frac{m^{2} - n^{2}}{2}$ ，中正确的是（）

A、①②③ B、①②④ C、①③ D、①②③④

查看试题解析

二、填空题

9. $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{99^{2}}) (1 - \frac{1}{100^{2}})$ =；

查看试题解析
10. 配方法是数学中非常重要的一种思想方法，它是指将一个式子或将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．这种方法常被用到代数式的变形中，并结合非负数的意义来解决问题．例如： $x^{2} - 4 x + 5$ 可配方成 ${(x - 2)}^{2} + 1$ ； $x^{2} + 2 x + 4$ 可配方成 ${(x + 1)}^{2} + 3$ ．若 $x^{2} + y^{2} - 2 x + 4 y + 5 = 0$ ，则 $x + y$ 的值为．

查看试题解析
11. 两个正方形的边长分别为a和b，且a+b=10，ab=22 ，那么阴影部分的面积是．

查看试题解析
12. 如图，阴影部分是边长是 $a$ 的大正方形剪去一个边长是 $b$ 的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，给出下列4幅图割拼方法中，其中能够验证平方差公式的有（填序号）

查看试题解析

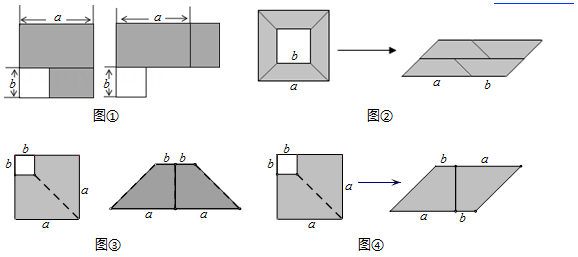
三、解答题

13. 【阅读理解】
完全平方公式： $(a \pm b)^{2} = a^{2} \pm 2 a b + b^{2}$ 适当的变形，可以解决很多的数学问题．

例：若 $a - b = 3 ， a b = 1$ ，求 $a^{2} + b^{2}$ 的值．

解：因为 $a - b = 3 ， a b = 1$ ，

所以 $(a - b)^{2} = 9 ， 2 a b = 2$ ，

所以 $(a - b)^{2} = a^{2} - 2 a b + b^{2} = 9$ ，

所以 $a^{2} + b^{2} = 11$ ．

根据上面的解题思路与方法，解决下列问题：

(1)、已知 $a - b = 4 ， a b = 5$ ，求 $a^{2} + b^{2}$ 和 $(a + b)^{2}$ 的值．

(2)、若 $x$ 满足 $(x - 2023)^{2} + (x - 2010)^{2} = 189$ ，求 $(x - 2023) (x - 2010)$ 的值；

查看试题解析
14. 公元3世纪，古希腊数学家丢番图（Diophantus）在其《算术》一书中设置了以下问题：已知两正整数之和为20，乘积为96，求这两个数．因为两数之和为20，所以这两个数不可能同时大于10，也不可能同时小于10，必定是一个大于10，一个小于10．根据如图所示的设法，可设一个数为 $10 + x$ ，则另一个数为 $10 - x$ ，根据两数之积为96，可得 $(10 + x) (10 - x) = 96$ ．请根据以上思路解决下列问题：

(1)、若两个正整数之和为100，大数比小数大 $2 a$ ，根据丢番图的设法，这两个正整数可表示为和；

(2)、请你根据丢番图的运算方法，计算 $502 \times 498$ 的值．

查看试题解析
15. 综合实践．
活动主题：探究图形面积与代数式之间的关系

活动资源：提供长度不同的两种木棒各 $4$ 根 $($ 如图 $)$

入项任务：运用以上 $8$ 根木棒 $($ 不折断 $)$ 摆成长方形或正方形，且木棒全部用完 $.$ 选取同学们的甲、乙、丙、丁四种不同的摆法 $($ 如图 $)$ 进行研究．

问题探究过程

(1)、发现问题：
请观察以上所有图形，并研究不同2种或2种以上 $)$ 摆法的图形面积之间关系，你发现哪些结论？
例如：小明发现：甲摆法的面积是乙摆法总面积的2倍．
小张发现：丁摆法的总面积大于乙摆法的总面积．
聪明的你，能提出不同于小明和小张的更创新更有意义问题吗？
你的发现是； $($ 请用简洁的语言描述 $)$

(2)、提出问题：
请用代数式表示你的发现 $($ 设两种木棒的长度分别为 $a$ ， $b ($ 其中 $a > b)$ ，四种图形面积分别为 $S_{甲}$ ， $S_{乙}$ ， $S_{丙}$ ， $S_{丁}$ ．
例如：小明的结论是 $S_{甲} = 2 S_{乙} = 4 a b$ ．
小张的结论是 $S_{丁} > S_{乙}$ ，
你的结论是：；

(3)、分析问题：
请用所学的数学知识证明你的结论．
例如：小明的证明方法如下．
证： $∵ S_{甲} = 2 a \times 2 b = 4 a b$ ， $S_{乙} = a b + a b = 2 a b$ ，
$∴ S_{甲} = 2 S_{乙}$ ，
你的证明：；

(4)、拓展创新：
把甲摆法围成大长方形纸片沿虚线剪成四个全等的小长方形，请用四个小长方形拼摆出边长为 $(a - b)$ 的正方形，画出示意图，并用等式表达示意图中的各图形面积之间的关系．
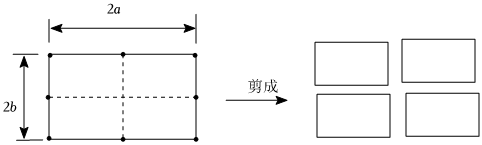
你的示意图：；
你的关系式：．

(5)、迁移应用：
根据以上的研究结论，请解决数学问题，若 $x + y = \sqrt{31}$ ， $x y = 7$ ，求 $x - y$ 的值．

你的解答：．

查看试题解析

【培优卷】2024年浙教版数学七年级下册3.4乘法公式 同步练习

一、选择题

二、填空题

三、解答题

【培优卷】2024年浙教版数学七年级下册3.4乘法公式同步练习