【2024中考数学一轮复习】06平面直角坐标系与函数基础巩固
试卷更新日期:2024-03-17 类型:一轮复习
一、选择题
-
1. 在平面直角坐标系中,点P(﹣3,2)在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在平面直角坐标系中,点到轴的距离是( )A、4 B、3 C、 D、3. 在平面直角坐标系内有一点P(x , y),若点P位于第二象限,并且点P到x轴和y轴的距离分别为5,2,则点P的坐标是( )A、(5,2) B、(2,5) C、(2,﹣5) D、(﹣2,5)4. 根据下列描述,能够确定一个点的位置的是( )A、省博物馆东侧 B、体育馆东面看台第排 C、第节车厢,号座位 D、学校图书馆前面5. 在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1) 关于x轴对称, 则a+b的值是( )A、1 B、2 C、3 D、46. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益部游戏.如图是一局象棋残局,已知表示棋子“马“和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
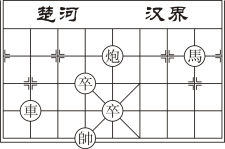 A、(2,3) B、(2,1) C、(1,2) D、(1,3)7. 在平面直角坐标系xOy中,点关于原点对称的点的坐标是( )A、 B、 C、 D、8. 已知点A在第二象限,到 x轴的距离是5,到y轴的距离是6,点A的坐标为( )A、 B、 C、 D、9. 在函数y= + 中,自变量x的取值范围是( )A、x<4 B、x≥4且x≠-3 C、x>4 D、x≤4且x≠-310. 函数中自变量x的取值范围在数轴上可表示为( )A、
A、(2,3) B、(2,1) C、(1,2) D、(1,3)7. 在平面直角坐标系xOy中,点关于原点对称的点的坐标是( )A、 B、 C、 D、8. 已知点A在第二象限,到 x轴的距离是5,到y轴的距离是6,点A的坐标为( )A、 B、 C、 D、9. 在函数y= + 中,自变量x的取值范围是( )A、x<4 B、x≥4且x≠-3 C、x>4 D、x≤4且x≠-310. 函数中自变量x的取值范围在数轴上可表示为( )A、 B、
B、 C、
C、 D、
D、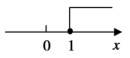 11. 下列图象中,y不是x的函数图象的是( )A、
11. 下列图象中,y不是x的函数图象的是( )A、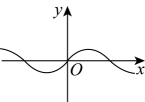 B、
B、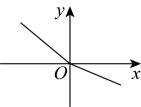 C、
C、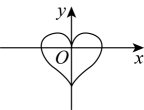 D、
D、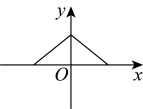 12. 骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化如图反映了骆驼的体温随时间的变化情况,下列说法错误的是( )
12. 骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化如图反映了骆驼的体温随时间的变化情况,下列说法错误的是( ) A、骆驼体温从最低上升到最高需要小时 B、骆驼体温一天内有两次达到 C、从时到时,骆驼的体温逐渐上升 D、第一天时与第二天时,骆驼的体温相同
A、骆驼体温从最低上升到最高需要小时 B、骆驼体温一天内有两次达到 C、从时到时,骆驼的体温逐渐上升 D、第一天时与第二天时,骆驼的体温相同二、填空题
-
13. 写出图中点P的坐标: . 点P到横轴的距离是 , 到纵轴的距离是
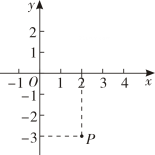 14. 若点M(m+3,m-1)在第四象限,则m的取值范围是.15. 在平面直角坐标系中,将点向右平移3个单位长度后,再向下平移2个单位长度,得到点 , 则点的坐标为 .16. 如图,将某动物园中的猴山,狮虎山,熊猫馆分别记为M,N,P,若建立平面直角坐标系,将猴山M,狮虎山N用坐标分别表示为(2,1)和(8,2),则熊猫馆P用坐标表示为.
14. 若点M(m+3,m-1)在第四象限,则m的取值范围是.15. 在平面直角坐标系中,将点向右平移3个单位长度后,再向下平移2个单位长度,得到点 , 则点的坐标为 .16. 如图,将某动物园中的猴山,狮虎山,熊猫馆分别记为M,N,P,若建立平面直角坐标系,将猴山M,狮虎山N用坐标分别表示为(2,1)和(8,2),则熊猫馆P用坐标表示为. 17. 直角坐标系中,点在第二象限,且到轴和轴的距离分别为 , , 则点的坐标为 .18. 函数中自变量的取值范围是 .19. 函数y= 中,自变量x的取值范围是 .20. 函数的自变量x的取值范围为.21. 函数y=中自变量的取值范围是.
17. 直角坐标系中,点在第二象限,且到轴和轴的距离分别为 , , 则点的坐标为 .18. 函数中自变量的取值范围是 .19. 函数y= 中,自变量x的取值范围是 .20. 函数的自变量x的取值范围为.21. 函数y=中自变量的取值范围是.三、解答题
-
22. 小倩和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴;只知道游乐园D的坐标为(2,﹣2).
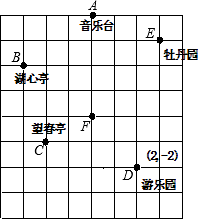 (1)、画出平面直角坐标系;(2)、求出其他各景点的坐标.23. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)、画出平面直角坐标系;(2)、求出其他各景点的坐标.23. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3). (1)、点C关于原点对称的点的坐标为 ;(2)、画出△ABC绕着点O按顺时针方向旋转90°得到的图形△A1B1C1 , 写出△A1B1C1各顶点的坐标.24. 对于平面直角坐标系xOy内的点P和图形M,给出如下定义:连接OP,过点O作OP的垂线OW,在垂线OW上取一点P′,使OP′=OP,点P′在图形M上或图形M围成的区域内,那么称点P是图形M关于原点O的“关联垂点”.已知点A(1,1),B(3,1),C(2,3).
(1)、点C关于原点对称的点的坐标为 ;(2)、画出△ABC绕着点O按顺时针方向旋转90°得到的图形△A1B1C1 , 写出△A1B1C1各顶点的坐标.24. 对于平面直角坐标系xOy内的点P和图形M,给出如下定义:连接OP,过点O作OP的垂线OW,在垂线OW上取一点P′,使OP′=OP,点P′在图形M上或图形M围成的区域内,那么称点P是图形M关于原点O的“关联垂点”.已知点A(1,1),B(3,1),C(2,3). (1)、在点P1(﹣1,0),P2(﹣1,1),P3(﹣1,2),P4(﹣1,3)中,点 是线段AB关于原点O的“关联垂点”(只填写字母);(2)、如果点D(m,2)是△ABC关于原点O的“关联垂点”,求m的取值范围.25. 为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费.现设一户居民每月用水x立方米,应缴水费y元.(1)、求出y关于x的函数表达式;(2)、若该市一户居民某月用水10立方米,求应缴水费;(3)、该市一户居民某月缴水费26.6元,求该户居民本月用水量.26. “珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次离家距离与所用的时间的关系示意图.
(1)、在点P1(﹣1,0),P2(﹣1,1),P3(﹣1,2),P4(﹣1,3)中,点 是线段AB关于原点O的“关联垂点”(只填写字母);(2)、如果点D(m,2)是△ABC关于原点O的“关联垂点”,求m的取值范围.25. 为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费.现设一户居民每月用水x立方米,应缴水费y元.(1)、求出y关于x的函数表达式;(2)、若该市一户居民某月用水10立方米,求应缴水费;(3)、该市一户居民某月缴水费26.6元,求该户居民本月用水量.26. “珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次离家距离与所用的时间的关系示意图.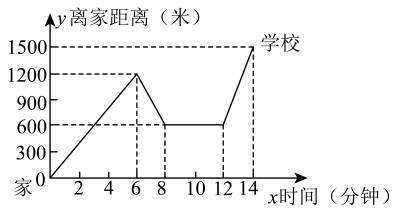
根据图中提供的信息回答下列问题:
(1)、小明家到学校的路程是米;他书店停留了分钟;(2)、本次上学途中,小明骑单车一共行驶了米;(3)、我们认为骑单车的速度超过300米/分钟就超越了安全限度.在整个上学的途中,请通过图像直接判断哪个时间段小明骑车速度最快?然后通过计算说明小明骑单车最快速度是否在安全限度内?27. 如图1是甲乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上,现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(cm)与注水时间x(min)之间的关系如图2所示,根据图象解答下列问题: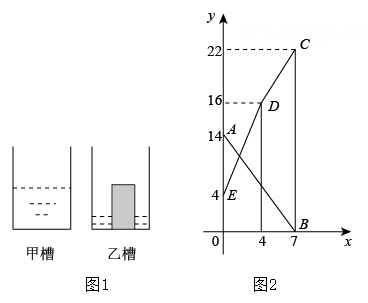 (1)、图2中折线EDC表示槽中水的深度与注水时间之间的关系;线段AB表示槽中水的深度与注水时间之间的关系;铁块的高度为cm.(2)、注水多长时间,甲、乙两个水槽中水的深度相同?28. 如图,表示振华商场一天的某型电脑销售额与销售量的关系,表示该商场一天的销售成本与电脑销售量的关系.观察图象,解决以下问题:
(1)、图2中折线EDC表示槽中水的深度与注水时间之间的关系;线段AB表示槽中水的深度与注水时间之间的关系;铁块的高度为cm.(2)、注水多长时间,甲、乙两个水槽中水的深度相同?28. 如图,表示振华商场一天的某型电脑销售额与销售量的关系,表示该商场一天的销售成本与电脑销售量的关系.观察图象,解决以下问题: (1)、当销售量时,销售额万元,销售成本万元;(2)、一天销售台时,销售额等于销售成本;(3)、分别求出和对应的函数表达式;(4)、直接写出利润与销售量之间的函数表达式,并求出当销售量是多少时,每天的利润达到5万元?
(1)、当销售量时,销售额万元,销售成本万元;(2)、一天销售台时,销售额等于销售成本;(3)、分别求出和对应的函数表达式;(4)、直接写出利润与销售量之间的函数表达式,并求出当销售量是多少时,每天的利润达到5万元?