【2024中考数学一轮复习】08反比例函数基础巩固
试卷更新日期:2024-03-17 类型:一轮复习
一、选择题
-
1. 反比例函数y= (x<0)的图象位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列关于反比例函数的描述中,不正确的是( )A、图象在第二、四象限 B、随的增大而增大 C、点在反比例函数的图象上 D、当时,3. 若点A(x₁,-2),B(x₂,1),C(x₃,2)都在反比例函数的图象上,则x₁,x₂,x₂的大小关系是( )A、 B、 C、 D、4. 已知函数y= , 下列说法:①函数图象分布在第一、三象限;②在每个象限内,y随x的增大而减小;③若A(x1 , y1) ,B(x2 , y2)两点在该函数图象上,且x1+x2=0,则y1 =y2 , 其中说法正确的个数是( )A、0 B、1 C、2 D、35. 点、、在反比例函数的图象上,且 , 则有( )A、 B、 C、 D、6. 从1,2,3这三个数中随机抽取两个不同的数,分别记作和.若点的坐标记作 , 则点在双曲线上的概率是( )A、 B、 C、 D、7. 在同一直角坐标系中,函数y=-kx+k与的大致图象可能为( )A、
 B、
B、 C、
C、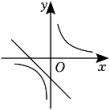 D、
D、 8. 如图,在直角坐标系中,一次函数与反比例函数的图象交于A , B两点,下列结论正确的是( )
8. 如图,在直角坐标系中,一次函数与反比例函数的图象交于A , B两点,下列结论正确的是( )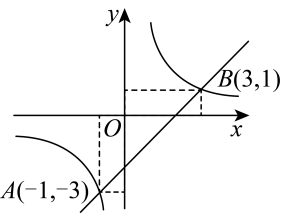 A、当时, B、当时, C、当时, D、当时,9. 已知,直线y=−2x+8与双曲线相交于点(m,n),则的值等于( )A、-2 B、2 C、-4 D、410. 如图,点A是反比例函数图象上任意一点,过点A分别作x轴,y轴的垂线,垂足为B , C , 则四边形OBAC的面积为( )
A、当时, B、当时, C、当时, D、当时,9. 已知,直线y=−2x+8与双曲线相交于点(m,n),则的值等于( )A、-2 B、2 C、-4 D、410. 如图,点A是反比例函数图象上任意一点,过点A分别作x轴,y轴的垂线,垂足为B , C , 则四边形OBAC的面积为( )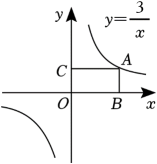 A、1.5 B、3 C、6 D、911. 关于反比例函数 ,下列说法错误的是( )A、图象位于第一、三象限 B、图象关于原点成中心对称 C、 D、12. 对于函数y= , 当x=2时,y=-5,则这个函数的表达式为( )A、y= B、y= C、y= D、y=
A、1.5 B、3 C、6 D、911. 关于反比例函数 ,下列说法错误的是( )A、图象位于第一、三象限 B、图象关于原点成中心对称 C、 D、12. 对于函数y= , 当x=2时,y=-5,则这个函数的表达式为( )A、y= B、y= C、y= D、y=二、填空题
-
13. 反比例函数的图象分布在第一、三象限内,则的取值范围为 .14. 反比例函数与一次函数交于点 , 则k的值为.15. 在平面直角坐标系中,正比例函数y=3x与反比例函数y= 的图象交于点A(a,﹣6),则k=.16. 如图,已知直线y=mx与双曲线y= 一个交点坐标为(3,4),则它们的另一个交点坐标是.
 17. 已知点 在直线 上,也在双曲线 上,则 的值为.18. 如图,点在反比例函数的图象上,轴于点 , 的面积为3,则的值为 .
17. 已知点 在直线 上,也在双曲线 上,则 的值为.18. 如图,点在反比例函数的图象上,轴于点 , 的面积为3,则的值为 . 19. 如图,A、B两点分别在反比例函数(x>0)和(x>0)的图象上,且ABx轴,C为x轴上任意一点,则△ABC的面积为 .
19. 如图,A、B两点分别在反比例函数(x>0)和(x>0)的图象上,且ABx轴,C为x轴上任意一点,则△ABC的面积为 .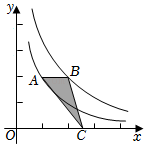 20. 如图所示,点A是反比例函数图象上的任意一点,轴交反比例函数的图象于点B,以为边作 , 点C,D在x轴上,则的面积为 .
20. 如图所示,点A是反比例函数图象上的任意一点,轴交反比例函数的图象于点B,以为边作 , 点C,D在x轴上,则的面积为 .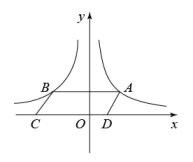
三、解答题
-
21. 如图,已知一次函数y1=kx+b与反比例函数y2= 的图象交于 、 两点.分别求出y1和y2的解析式.
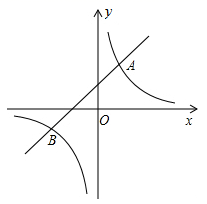 22. 已知一次函数y1=﹣x+7的图象与反比例函数y2=图象交于A、B两点,且A点的横坐标﹣1,求:
22. 已知一次函数y1=﹣x+7的图象与反比例函数y2=图象交于A、B两点,且A点的横坐标﹣1,求: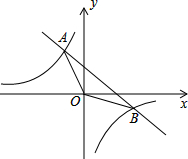 (1)、反比例函数的解析式.(2)、△AOB的面积.(3)、直接写出满足y1≤y2时x的取值范围.23. 如图,一次函数图象与反比例函数图象交于点A(-1,6),B( , a-3),与x轴交于点C,与y轴交于点D.
(1)、反比例函数的解析式.(2)、△AOB的面积.(3)、直接写出满足y1≤y2时x的取值范围.23. 如图,一次函数图象与反比例函数图象交于点A(-1,6),B( , a-3),与x轴交于点C,与y轴交于点D. (1)、求反比例函数与一次函数的表达式;(2)、点M在x轴上,若S△OAM=S△OAB , 求点M的坐标.24. 如图,已知一次函数: y₁=kx+b(k≠0)与反比例函数 的图象在第一、三象限分别相交于点A(3,4),B(a,-2),直线AB与y轴、x轴分别相交于点C,D.
(1)、求反比例函数与一次函数的表达式;(2)、点M在x轴上,若S△OAM=S△OAB , 求点M的坐标.24. 如图,已知一次函数: y₁=kx+b(k≠0)与反比例函数 的图象在第一、三象限分别相交于点A(3,4),B(a,-2),直线AB与y轴、x轴分别相交于点C,D.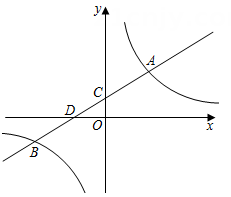 (1)、求一次函数和反比例函数的表达式.(2)、比较大小:ADBC(填“>”“<”或“=”).(3)、直接写出当y₁<y₂时,x的取值范围.'25. 如图,直线y=kx+2与双曲线y=相交于点A,B,已知点A的横坐标为1.
(1)、求一次函数和反比例函数的表达式.(2)、比较大小:ADBC(填“>”“<”或“=”).(3)、直接写出当y₁<y₂时,x的取值范围.'25. 如图,直线y=kx+2与双曲线y=相交于点A,B,已知点A的横坐标为1.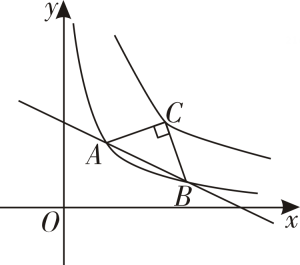 (1)、求直线y=kx+2的表达式及点B的坐标;(2)、以线段AB为斜边在直线AB的上方作等腰直角三角形ABC.求经过点C的双曲线的表达式26. 如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(-1,4),B(a,-1)两点
(1)、求直线y=kx+2的表达式及点B的坐标;(2)、以线段AB为斜边在直线AB的上方作等腰直角三角形ABC.求经过点C的双曲线的表达式26. 如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(-1,4),B(a,-1)两点 (1)、求反比例函数和一次函数的表达式;(2)、点P(n,0)在x轴负半轴上,连结AP,过点B作BQ∥AP,交y=的图象于点Q,连结PQ.当BQ=AP时,若四边形APQB的面积为36,求n的值27. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=(x>0)的图象上,点D的坐标为(4,3).
(1)、求反比例函数和一次函数的表达式;(2)、点P(n,0)在x轴负半轴上,连结AP,过点B作BQ∥AP,交y=的图象于点Q,连结PQ.当BQ=AP时,若四边形APQB的面积为36,求n的值27. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=(x>0)的图象上,点D的坐标为(4,3).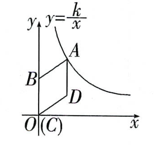 (1)、求k的值.(2)、若将菱形ABCD沿x轴正方向平移m个单位.
(1)、求k的值.(2)、若将菱形ABCD沿x轴正方向平移m个单位.①当菱形的顶点B落在反比例函数的图象上时,求m的值;
②在平移过程中,若反比例函数图象与菱形的边AD始终有交点,求m的取值范围.
28. 如图是函数 与函数 在第一象限内的图象,点P是 的图象上一动点,PA⊥x轴于点A , 交 的图象于点C, PB⊥y轴于点B , 交 的图象于点D. (1)、求证:D是BP的中点;(2)、求出四边形ODPC的面积.
(1)、求证:D是BP的中点;(2)、求出四边形ODPC的面积.