【2024中考数学一轮复习】09二次函数基础巩固
试卷更新日期:2024-03-17 类型:一轮复习
一、选择题
-
1. 抛物线y=(x-1)2+2的顶点坐标是( )A、(-1,2) B、(1,2) C、(-1,-2) D、(1,-2)2. 已知抛物线下列结论错误的是( )A、抛物线开口向上 B、抛物线的对称轴为直线x=2 C、抛物线的顶点坐标为(2,1) D、当x<2时,y随x的增大而增大3. 二次函数 的最小值是 ( )A、 2 B、2 C、 1 D、14. 若为二次函数图象上的三点,则的大小关系为( )A、 B、 C、 D、5. 下列图象中,是二次函数的图象的是( )A、
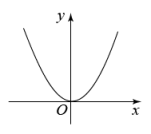 B、
B、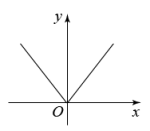 C、
C、 D、
D、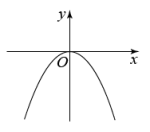 6. 若抛物线的顶点在第二象限,则的取值范围是( )A、 B、 C、 D、7. 二次函数的图像如图所示,下列结论中正确的是( ).
6. 若抛物线的顶点在第二象限,则的取值范围是( )A、 B、 C、 D、7. 二次函数的图像如图所示,下列结论中正确的是( ). A、 B、 C、 D、8. 如图,抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,下列结论不正确的是( )
A、 B、 C、 D、8. 如图,抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,下列结论不正确的是( ) A、3a+c>0 B、2a+b=0 C、abc>0 D、4a+2b+c<09. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度后,得到抛物线的解析式为( )A、 B、 C、 D、10. 将抛物线向下平移,关于平移前后的抛物线,下列说法正确的是( )A、开口方向改变 B、开口大小改变 C、对称轴不变 D、顶点位置不变11. 如图,用水管从某栋建筑物2.25m高的窗口A 处向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )
A、3a+c>0 B、2a+b=0 C、abc>0 D、4a+2b+c<09. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度后,得到抛物线的解析式为( )A、 B、 C、 D、10. 将抛物线向下平移,关于平移前后的抛物线,下列说法正确的是( )A、开口方向改变 B、开口大小改变 C、对称轴不变 D、顶点位置不变11. 如图,用水管从某栋建筑物2.25m高的窗口A 处向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )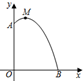 A、2.5米 B、3米 C、3.5米 D、4米12.
A、2.5米 B、3米 C、3.5米 D、4米12.如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( )
 A、60m2 B、63m2 C、64m2 D、66m213. 将二次函数y=x2-2x+3化为y=(x-m)2+k的形式,结果为( )A、y=(x+1)2+4 B、y=(x+1)2+2 C、y=(x-1)2+4 D、y=(x-1)2+214. 如下表中列出了二次函数的一些对应值,则一元二次方程的其中一个近似解的范围是( )
A、60m2 B、63m2 C、64m2 D、66m213. 将二次函数y=x2-2x+3化为y=(x-m)2+k的形式,结果为( )A、y=(x+1)2+4 B、y=(x+1)2+2 C、y=(x-1)2+4 D、y=(x-1)2+214. 如下表中列出了二次函数的一些对应值,则一元二次方程的其中一个近似解的范围是( )x
…
0
1
…
y
…
1
1
…
A、 B、 C、 D、15. 在平面直角坐标系 中,二次函数 的图象如图所示,则方程 的根的情况是 A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断
A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断二、填空题
-
16. 一种礼炮的升空高度与飞行时间的关系式是 , 若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为s.17. 二次函数y=x2+bx+c的图象如图所示,则下列结论:①b<0;②c>0;③b2﹣4ac>0;④a﹣b+c>0,其中正确的个数是个.
 18. 雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞如图 , 可以发现数学的研究对象一一抛物线在如图所示的平面直角坐标系中,伞柄在轴上,坐标原点为伞骨、的交点点为抛物线的顶点,点、在抛物线上,、关于轴对称分米,点到轴的距离是分米,、两点之间的距离是分米分别延长、交抛物线于点、 , 则雨伞撑开时的最大直径的长为 分米.
18. 雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞如图 , 可以发现数学的研究对象一一抛物线在如图所示的平面直角坐标系中,伞柄在轴上,坐标原点为伞骨、的交点点为抛物线的顶点,点、在抛物线上,、关于轴对称分米,点到轴的距离是分米,、两点之间的距离是分米分别延长、交抛物线于点、 , 则雨伞撑开时的最大直径的长为 分米. 19. 是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图建立平面直角坐标系,则抛物线的关系式是 .
19. 是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图建立平面直角坐标系,则抛物线的关系式是 . 20. 在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为y=-x2+x+ , 由此可知小宇此次实心球训练的成绩为米.
20. 在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为y=-x2+x+ , 由此可知小宇此次实心球训练的成绩为米.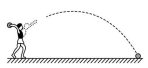
三、解答题
-
21. 如图,二次函数的图象与轴交于 , 两点,顶点为 .
 (1)、求此二次函数的解析式.(2)、 求的面积.22. 在平面直角坐标系中,抛物线y=x2+bx﹣3的对称轴为直线x=1.(1)、求这条抛物线的解析式.(2)、当﹣1≤x≤4时,求y的最大值和最小值.(3)、点P为这条抛物线上的一个动点,点P的横坐标为m(m>0),以点P为中心作正方形ABCD,AB=2m,且AB⊥x轴.
(1)、求此二次函数的解析式.(2)、 求的面积.22. 在平面直角坐标系中,抛物线y=x2+bx﹣3的对称轴为直线x=1.(1)、求这条抛物线的解析式.(2)、当﹣1≤x≤4时,求y的最大值和最小值.(3)、点P为这条抛物线上的一个动点,点P的横坐标为m(m>0),以点P为中心作正方形ABCD,AB=2m,且AB⊥x轴.
①当抛物线落在正方形内部的点的纵坐标y随x的增大而减小时,求m的取值范围.②正方形ABCD的边与抛物线只有两个交点,且交点的纵坐标之差为时,直接写出m的值.
23. 已知二次函数图象的顶点坐标是 , 且经过点 .(1)、求这个二次函数的表达式;(2)、若点在该函数图象上,求点的坐标.24. 如图,已知抛物线y=﹣x2+mx+3经过点M(﹣2,3).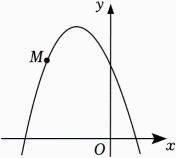 (1)、求m的值,并求出此抛物线的顶点坐标;(2)、当﹣3≤x≤0时,直接写出y的取值范围.25. 椒江某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价5元,那么平均可多售出10件.(1)、设每件童装降价x元时,每天可销售 件,每件盈利 元;(用x的代数式表示)(2)、每件童装降价多少元时,平均每天盈利1200元.(3)、设专卖店每天销售这款童装可获利润W元,当x为多少时W最大,最大值是多少?26. 如图,某单位拟在一块空地上修建矩形植物园ABCD,其中一边靠墙,可利用的墙长不超过16米,另外三边由36米长的栅栏围成,设矩形ABCD中,垂直于墙的边米,面积为y平方米.
(1)、求m的值,并求出此抛物线的顶点坐标;(2)、当﹣3≤x≤0时,直接写出y的取值范围.25. 椒江某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价5元,那么平均可多售出10件.(1)、设每件童装降价x元时,每天可销售 件,每件盈利 元;(用x的代数式表示)(2)、每件童装降价多少元时,平均每天盈利1200元.(3)、设专卖店每天销售这款童装可获利润W元,当x为多少时W最大,最大值是多少?26. 如图,某单位拟在一块空地上修建矩形植物园ABCD,其中一边靠墙,可利用的墙长不超过16米,另外三边由36米长的栅栏围成,设矩形ABCD中,垂直于墙的边米,面积为y平方米. (1)、y与x之间的函数关系式为 , 自变量x的取值范围为;(2)、若矩形ABCD的面积为154平方米,求x的值;(3)、当矩形ABCD的面积最大时,利用的墙长是多少米?并求此时的最大面积.27. 第31届世界大学生夏季运动会将于2023年7月28日至8月8日在成都举行,大熊猫是成都最具特色的对外传播标识物和“品牌图腾”,是天府之国享有极高知名度的个性名片.此次成都大运会吉祥物“蓉宝”(如图1)便是以熊猫基地真实的大熊猫“芝麻”为原型创作的.某商店销售“蓉宝”的公仔毛绒玩具,进价为30元/件,经市场调查发现:该商品的月销售量y(件)与销售价x(元/件)之间的关系如图2所示.
(1)、y与x之间的函数关系式为 , 自变量x的取值范围为;(2)、若矩形ABCD的面积为154平方米,求x的值;(3)、当矩形ABCD的面积最大时,利用的墙长是多少米?并求此时的最大面积.27. 第31届世界大学生夏季运动会将于2023年7月28日至8月8日在成都举行,大熊猫是成都最具特色的对外传播标识物和“品牌图腾”,是天府之国享有极高知名度的个性名片.此次成都大运会吉祥物“蓉宝”(如图1)便是以熊猫基地真实的大熊猫“芝麻”为原型创作的.某商店销售“蓉宝”的公仔毛绒玩具,进价为30元/件,经市场调查发现:该商品的月销售量y(件)与销售价x(元/件)之间的关系如图2所示. (1)、 求y关于x的函数解析式;(2)、由于某种原因,该商品进价提高了a元/件(),如果规定该玩具售价不超过40元/件,该商品在今后的销售中,月销售量与销售价仍然满足(1)中的函数关系,若该商品的月销售最大利润是2400元,求a的值.28. 调查了某城市近20个月的商品房价格,与上年同期相比,房价增长率y(%)与月份序号x近似地满足二次函数关系y=-0.25x2+3x.(1)、哪个月房价年增长率最高?哪几个月房价年增长率y随x的增加而增加?(2)、第几个月房价相当于上年同期水平?
(1)、 求y关于x的函数解析式;(2)、由于某种原因,该商品进价提高了a元/件(),如果规定该玩具售价不超过40元/件,该商品在今后的销售中,月销售量与销售价仍然满足(1)中的函数关系,若该商品的月销售最大利润是2400元,求a的值.28. 调查了某城市近20个月的商品房价格,与上年同期相比,房价增长率y(%)与月份序号x近似地满足二次函数关系y=-0.25x2+3x.(1)、哪个月房价年增长率最高?哪几个月房价年增长率y随x的增加而增加?(2)、第几个月房价相当于上年同期水平?