【2024中考数学一轮复习】11三角形基础巩固

试卷更新日期：2024-03-17 类型：一轮复习

进入出卷网下载

一、选择题

1. 长度分别为a，2，4的三条线段能组成一个三角形，则a的值可能是（）.

A、1 B、2 C、3 D、6

查看试题解析
2. 如图，CD⊥AB于点D，已知∠ABC是钝角，则（）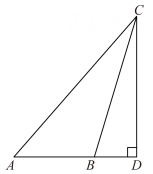

A、线段CD是△ABC的AC边上的高线 B、线段CD是△ABC的AB边上的高线 C、线段AD是△ABC的BC边上的高线 D、线段AD是△ABC的AC边上的高线

查看试题解析
3. 一次数学活动中，小明对纸带沿AB折叠，量得 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为（）

A、 $50 °$ B、 $60 °$ C、 $70 °$ D、 $80 °$

查看试题解析
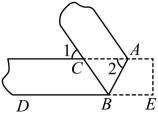4. 如图，在△ABC中，D是BC延长线上一点，∠B＝30°，∠ACD＝110°，则∠A等于（）

A、60° B、70° C、80° D、90°

查看试题解析
5. 如图，M，N分别是△ABC的边AB，AC的中点，若∠A=65°，∠ANM=45°，则∠B的度数为（）

A、20° B、45° C、65° D、70°

查看试题解析
6. 如图，菱形 $A B C D$ 中， $E ， F$ 分别是 $A B ， A C$ 的中点，若菱形 $A B C D$ 的周长为 $24$ ，则 $E F$ 的长为（）

A、 $6$ B、 $8$ C、 $3$ D、 $4$

查看试题解析
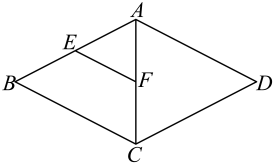7. 一副三角板如图摆放，则 $∠ α$ 的值是（）

A、125° B、100° C、115° D、105°

查看试题解析
8. 下列命题中，假命题的是（）

A、等腰三角形的两个底角相等 B、直角三角形的两个锐角互余 C、有两个内角是 60°的三角形是等边三角 D、等腰三角形的两个底角的平分线互相垂直

查看试题解析
9. 如图，等边 $△ A B C$ 中， $A B = 6$ ，点 $P$ 是 $B C$ 边上一点，则 $A P$ 的最小值是（）

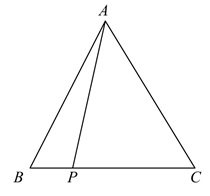A、3 B、4 C、5 D、 $3 \sqrt{3}$

查看试题解析
10. 等边三角形的对称轴有（）条

A、2 B、3 C、4 D、1

查看试题解析
11. 在 $△ A B C$ 中， $∠ A ： ∠ B ： ∠ C = 3 ： 2 ： 1$ ，则这个三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定

查看试题解析
12. 如图，已知AC⊥BC于点C，CD⊥AB于点D，∠A=56°，则∠DCB的度数是（）

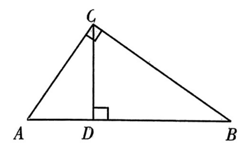A、30° B、45° C、56° D、60°

查看试题解析
13. 如图，湖的两岸有A，C两点，在与AC成直角的BC方向上的点C处测得AB＝15米，BC＝12米，则A，C两点间的距离为（）

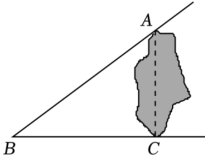A、3米 B、6米 C、9米 D、10米

查看试题解析
14. 下列各组数中，是勾股数的是（）

A、 $3$ ， $4$ ， $5$ B、 $1$ ， $2$ ， $3$ C、 $8$ ， $10$ ， $16$ D、 $5$ ， $10$ ， $13$

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ ，且 $B C = 4$ ，则BD长为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

16. 三角形两边的长分别是3和4，第三边的长是方程 $x^{2} - 12 x + 35 = 0$ 的根，则该三角形的周长为

查看试题解析
17. 如图，一副常规直角三角板叠放在一起，则图中 $∠ α$ 的度数为．

查看试题解析
18. 如图，把一块三角板的 $60 °$ 角的顶点放在直尺的一边上，若 $∠ 1 = 65 °$ ，则 $∠ 2$ 的度数是．

查看试题解析
19. 如图，在△ABC中，已知∠A为钝角，边AB，AC的中垂线分别交BC于点D，E．若BD²+CE²=DE² ，则∠A= ．

查看试题解析
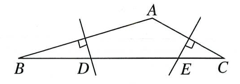20. 如图，已知平行四边形对角线AC、BD相交于点O，点E、F分别是线段AO、BO的中点．若AC+BD＝26cm，△OAB的周长是16cm，则EF＝cm．

查看试题解析
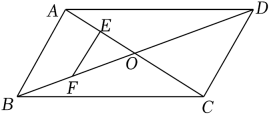21. 如图是一个残缺不全的三角形纸片，小明通过测量发现AB＝10cm，∠CAB＝∠DBA＝60°，则三角形纸片破损前的周长为 cm．

查看试题解析
22. 给出五种图形：①矩形；②菱形；③等腰三角形(腰与底边不相等)；④等边三角形；⑤平行四边形(不含矩形、菱形)，其中可用两块能完全重合的含有30°角的三角板拼成的所有图形是．

查看试题解析
23. 如图，点 $P$ 在 $∠ A O B$ 内，因为 $P M ⊥ O A$ ， $P N ⊥ O B$ ，垂足分别是 $M$ 、 $N$ ， $P M = P N$ ，所以 $O P$ 平分 $∠ A O B$ ，理由是．

查看试题解析
24. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 60 °$ ， $B C = 4 c m$ ，则 $A B =$ $c m$ ．

查看试题解析

三、解答题

25. 如图， $△ A B C ≅ △ D E B$ ，点E在边 $A B$ 上， $D E$ 与 $A C$ 相交于点 $F$ ．若 $D E = 9 ， B C = 4$ ， $∠ D = 2 5^{∘} ， ∠ C = 7 0^{∘}$ ．

(1)、求线段 $A E$ 的长；

(2)、求 $∠ D B C$ 的度数．

查看试题解析
26. 如图，AB=AC，DB = DC，则△ABD≌△ACD．完成下面的推理过程（填空）．
解：在△ABD和△ACD中，
∵AB=    ▲     （已知），
DB=DC（  ），
AD=    ▲     （公共边），
∴△ABD≌△ACD（）

查看试题解析
27. 在 $△ A B C$ 中， $D$ 是边 $A B$ 上一点， $E$ 是边 $A C$ 的中点，作 $C F ∥ A B$ 交 $D E$ 的延长线于点 $F$ ．

(1)、证明： $△ A D E ≌ △ C F E$ ．

(2)、若 $A B = A C$ ， $C E = 6$ ， $C F = 8$ ，求 $D B$ 的长．

查看试题解析
28. 如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 6 c m$ ， $B C = 8 c m$ ，点 $P$ 从 $A$ 点出发沿 $A B$ 边向 $B$ 以 $1 c m / s$ 的速度移动，点 $Q$ 从 $B$ 点出发沿 $B C$ 向 $C$ 点以 $2 c m / s$ 的速度移动，当其中一个点到达终点时两个点同时停止运动，请回答：

(1)、经过多少时间， $△ P B Q$ 的面积是 $5 c m^{2}$ ，此时， $P Q$ 长为多少 $c m$ ．

(2)、探究：是否存在某一时刻 $t$ ，使 $S_{四边形 A P Q C} = \frac{5}{12} S_{△ A B C}$ ，如果存在，求出 $t$ 的值；如果不存在，请说明理由．

查看试题解析