【2024中考数学一轮复习】12解直角三角形基础巩固
试卷更新日期:2024-03-17 类型:一轮复习
一、选择题
-
1. 如图,在中, , 下列结论中正确的是( )
 A、 B、 C、 D、2. 在Rt△ABC中,各边都扩大5倍,则角A的三角函数值( )
A、 B、 C、 D、2. 在Rt△ABC中,各边都扩大5倍,则角A的三角函数值( )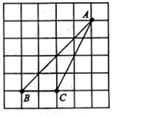 A、不变 B、扩大5倍 C、缩小5倍 D、不能确定3. 在Rt△ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为( )A、 B、 C、 D、4. 若 ,则 的大小是( )A、30° B、45° C、60° D、75°5. 如图是的高, , , , 则的长为( ).
A、不变 B、扩大5倍 C、缩小5倍 D、不能确定3. 在Rt△ABC中,∠C=90°,如果AC=4,BC=3,那么∠A的正切值为( )A、 B、 C、 D、4. 若 ,则 的大小是( )A、30° B、45° C、60° D、75°5. 如图是的高, , , , 则的长为( ).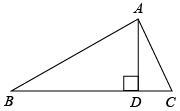 A、 B、 C、 D、6. 如图,是电杆的一根拉线,测得米, , 则拉线的长为( )
A、 B、 C、 D、6. 如图,是电杆的一根拉线,测得米, , 则拉线的长为( )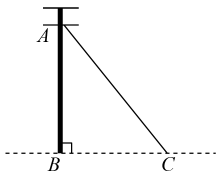 A、米 B、米 C、米 D、米7. 图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,和分别是两根不同长度的支撑杆,其中两支脚 , 展开角 , 晾衣臂 , 则支樟杆的端点离地面的高度为( )
A、米 B、米 C、米 D、米7. 图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,和分别是两根不同长度的支撑杆,其中两支脚 , 展开角 , 晾衣臂 , 则支樟杆的端点离地面的高度为( )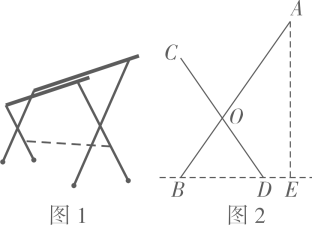 A、 B、 C、 D、8. 如图,滑雪场有一坡角为20°的滑道,滑雪道的长AC为100米,则BC的长为( )米.
A、 B、 C、 D、8. 如图,滑雪场有一坡角为20°的滑道,滑雪道的长AC为100米,则BC的长为( )米. A、 B、100cos20° C、 D、100sin20°9. 如图,河坝横断面迎水坡AB的坡比为1: , 坝高BC=4m,则AB的长度为( )
A、 B、100cos20° C、 D、100sin20°9. 如图,河坝横断面迎水坡AB的坡比为1: , 坝高BC=4m,则AB的长度为( )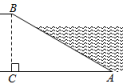 A、2m B、4m C、4m D、6m10. 计算sin 45°+cos45°的值为( )A、1 B、2 C、 D、211. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α , ∠ADC=β , 则竹竿AB与AD的长度之比为( )
A、2m B、4m C、4m D、6m10. 计算sin 45°+cos45°的值为( )A、1 B、2 C、 D、211. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α , ∠ADC=β , 则竹竿AB与AD的长度之比为( )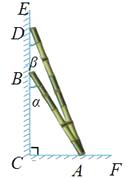 A、 B、 C、 D、12. 如图,若△ABC底边BC上的高为h1 , △DEF底边EF上的高为h2 , 则h1与h2的大小关系是( )
A、 B、 C、 D、12. 如图,若△ABC底边BC上的高为h1 , △DEF底边EF上的高为h2 , 则h1与h2的大小关系是( )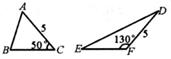 A、h1=h2 B、h1<h2 C、h1>h2 D、以上都有可能13. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )
A、h1=h2 B、h1<h2 C、h1>h2 D、以上都有可能13. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )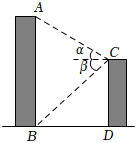 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
14. 在Rt△ABC中,∠C=90°,sinA= ,则cosA=.
15. 计算cos260°+sin260°的值为.16. 在Rt△ABC中,∠C=90,sinA= ,则sinB=.17. 如图,在 8×4 的矩形网格中,每个小正方形的边长都是 1,若 的三个顶点在图中相应的格点上,则 的值为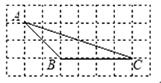 18. 计算;sin30°•tan30°+cos60°•tan60°= .19. 某水库大坝横截面示意图如下所示,其中AB,CD分别表示水库下底面、上底面的水平线,∠ABC=120°,BC的长是50m,则水库大坝的高度h=.
18. 计算;sin30°•tan30°+cos60°•tan60°= .19. 某水库大坝横截面示意图如下所示,其中AB,CD分别表示水库下底面、上底面的水平线,∠ABC=120°,BC的长是50m,则水库大坝的高度h=.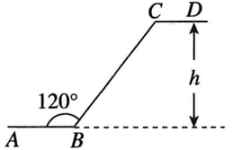 20.
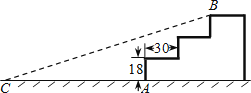
20.如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是cm.
 21. 如图,河岸AD,BC互相平行,桥AB垂直于两岸,从C处看桥的两端A,B,夹角∠BCA=60°,测得BC=14m,则桥长AB=m(结果精确到1m).
21. 如图,河岸AD,BC互相平行,桥AB垂直于两岸,从C处看桥的两端A,B,夹角∠BCA=60°,测得BC=14m,则桥长AB=m(结果精确到1m).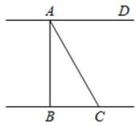 22. 某校九年级的一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在A处测得新教学楼房顶B点的仰角为45°,走6米到C处再测得B点的仰角为55°,已知O、A、C在同一条直线上,则新教学楼的高度OB是米.(结果根据“四舍五入”法保留小数点后两位)(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
22. 某校九年级的一位同学,想利用刚刚学过的三角函数知识测量新教学楼的高度,如图,她在A处测得新教学楼房顶B点的仰角为45°,走6米到C处再测得B点的仰角为55°,已知O、A、C在同一条直线上,则新教学楼的高度OB是米.(结果根据“四舍五入”法保留小数点后两位)(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)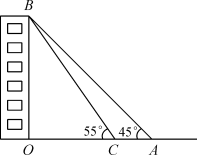 23. 在数学实践活动课上,某兴趣小组测量操场上篮球筐距地面的高度如图所示,已知篮球筐的直径AB约为0.45m,某同学站在C处,先仰望篮球筐直径的一端A处,测得仰角为42°,再调整视线,测得篮球筐直径的另一端B处的仰角为35°.若该同学的目高OC为1.7m,则篮球筐距地面的高度AD大约是m.(结果精确到1m).(参考数据:tan42°≈0.9,tan35°=0.7,tan48°≈1.1,tan55°≈1.4)
23. 在数学实践活动课上,某兴趣小组测量操场上篮球筐距地面的高度如图所示,已知篮球筐的直径AB约为0.45m,某同学站在C处,先仰望篮球筐直径的一端A处,测得仰角为42°,再调整视线,测得篮球筐直径的另一端B处的仰角为35°.若该同学的目高OC为1.7m,则篮球筐距地面的高度AD大约是m.(结果精确到1m).(参考数据:tan42°≈0.9,tan35°=0.7,tan48°≈1.1,tan55°≈1.4)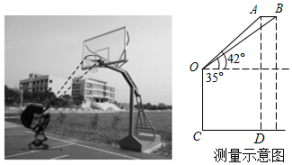
三、解答题
-
24. 如图,四边形ABCD中,∠ADB=∠DBC=90°,AD=6,CD=12,tanA= ,求sinC的值.
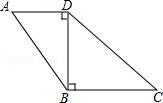 25. 为建设美好公园社区, 增强民众生活幸福感, 如图 1, 某社区服务中心在文化活动室墙外安装遮阳篷, 便于社区居民休想. 在如图 2 的侧面示意图中, 遮阳篷靠墙端离地高记为 B C, 遮阳篷 A B 长为 5 米, 与水平面的夹角为 .
25. 为建设美好公园社区, 增强民众生活幸福感, 如图 1, 某社区服务中心在文化活动室墙外安装遮阳篷, 便于社区居民休想. 在如图 2 的侧面示意图中, 遮阳篷靠墙端离地高记为 B C, 遮阳篷 A B 长为 5 米, 与水平面的夹角为 .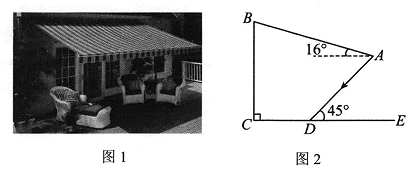 (1)、求点A到墙面BC的距离;(2)、当太阳光线AD与地面CE的夹角为45°时,量得影长CD为1.8米,求遮阳篷靠墙端离地高BC的长.(结果精确到0.1米;参考数据: sin16°≈0.28,cos16°≈0.96,tan16° ≈0.29 )26. 如图,兰兰在山坡A处放风筝,在A点观察风筝P的仰角为37 , 风筝线PA的长为20米,已知山坡的坡角 , 米,求风筝P距离地面BC的高度(参考数据: , , , ).
(1)、求点A到墙面BC的距离;(2)、当太阳光线AD与地面CE的夹角为45°时,量得影长CD为1.8米,求遮阳篷靠墙端离地高BC的长.(结果精确到0.1米;参考数据: sin16°≈0.28,cos16°≈0.96,tan16° ≈0.29 )26. 如图,兰兰在山坡A处放风筝,在A点观察风筝P的仰角为37 , 风筝线PA的长为20米,已知山坡的坡角 , 米,求风筝P距离地面BC的高度(参考数据: , , , ).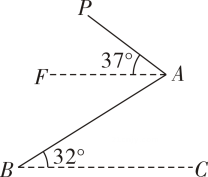 27. 小瑞放学后回家,到小区的门口C处时,看到自己家的窗户A的仰角 , 他向前走了后到达点D处时,看到自己家窗户A的仰角 , 小瑞的身高 , 求小瑞家到地面的高度 . (结果取整数,参考数据: , , , , , , )
27. 小瑞放学后回家,到小区的门口C处时,看到自己家的窗户A的仰角 , 他向前走了后到达点D处时,看到自己家窗户A的仰角 , 小瑞的身高 , 求小瑞家到地面的高度 . (结果取整数,参考数据: , , , , , , )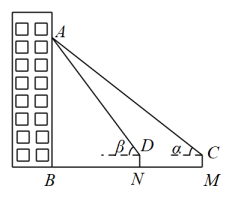 28. 如图,线段 表示信号塔, 表示一斜坡, .且点 三点在同一水平线上,点 在同一平面内,斜坡 的坡比为 米.某人站在坡顶D处测得塔顶A点的仰角为37°,站在坡底C处测得塔顶A点的仰角为48°(人的身高忽略不计),求信号塔的高度 (结果精确到1米).(参考数据: , ).
28. 如图,线段 表示信号塔, 表示一斜坡, .且点 三点在同一水平线上,点 在同一平面内,斜坡 的坡比为 米.某人站在坡顶D处测得塔顶A点的仰角为37°,站在坡底C处测得塔顶A点的仰角为48°(人的身高忽略不计),求信号塔的高度 (结果精确到1米).(参考数据: , ).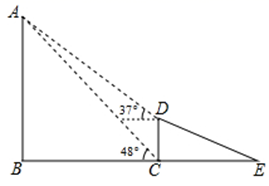 29. 如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物 的高度,他们先在斜坡上的 处,测得建筑物顶端 的仰角为30°.且 离地面的高度 .坡底 ,然后在 处测得建筑物顶端 的仰角是60°,点 、 、 在同一水平线上,求建筑物 的高.(结果用含有根号的式子表示)
29. 如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物 的高度,他们先在斜坡上的 处,测得建筑物顶端 的仰角为30°.且 离地面的高度 .坡底 ,然后在 处测得建筑物顶端 的仰角是60°,点 、 、 在同一水平线上,求建筑物 的高.(结果用含有根号的式子表示)