【2024中考数学一轮复习】13四边形基础巩固
试卷更新日期:2024-03-17 类型:一轮复习
一、选择题
-
1. 如图,若 , 则下列结论正确的是( )
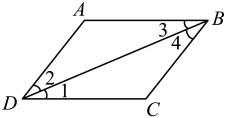 A、∠1=∠2 B、∠2=∠3 C、∠1=∠3 D、∠2=∠42. 下列说法正确的是( )A、邻边相等的平行四边形是矩形 B、矩形的对角线互相平分 C、对角线互相垂直的四边形是菱形 D、一组对边相等,另一组对边平行的四边形是平行四边形3. 如图,在平行四边形ABCD中,E,F分别在边BC,AD上,添加选项中的条件后不能判定四边形AECF是平行四边形的是( ).
A、∠1=∠2 B、∠2=∠3 C、∠1=∠3 D、∠2=∠42. 下列说法正确的是( )A、邻边相等的平行四边形是矩形 B、矩形的对角线互相平分 C、对角线互相垂直的四边形是菱形 D、一组对边相等,另一组对边平行的四边形是平行四边形3. 如图,在平行四边形ABCD中,E,F分别在边BC,AD上,添加选项中的条件后不能判定四边形AECF是平行四边形的是( ).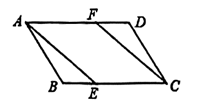 A、BE = DF B、AECF C、AF = EC D、AE = EC4. 如图,在平行四边形ABCD中,都不一定成立的是( )
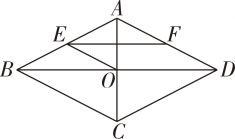
A、BE = DF B、AECF C、AF = EC D、AE = EC4. 如图,在平行四边形ABCD中,都不一定成立的是( )①AO=CO;②AC⊥BD;③AD∥BC;④∠CAB=∠CAD.
 A、①和④ B、②和③ C、③和④ D、②和④5. 如图,在△ABC中,∠C=90°, AC=8, BC=6,点P为斜边AB上一动点,过点P作PE⊥Ac于点E, PF⊥BC于点F,连结EF,则线段EF的最小值为( )
A、①和④ B、②和③ C、③和④ D、②和④5. 如图,在△ABC中,∠C=90°, AC=8, BC=6,点P为斜边AB上一动点,过点P作PE⊥Ac于点E, PF⊥BC于点F,连结EF,则线段EF的最小值为( )
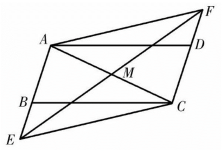
 A、1.2 B、2.4 C、2.5 D、4.86. 如图,在平行四边形ABCD中,AB= , AD=2,连接AC,BD相交于点O,E为BC的中点,若BD= , 则四边形OECD的面积为( )
A、1.2 B、2.4 C、2.5 D、4.86. 如图,在平行四边形ABCD中,AB= , AD=2,连接AC,BD相交于点O,E为BC的中点,若BD= , 则四边形OECD的面积为( )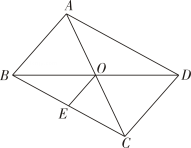 A、 B、 C、 D、7. 一次数学活动中,小明对纸带沿AB折叠,量得 , 则的度数为( )
A、 B、 C、 D、7. 一次数学活动中,小明对纸带沿AB折叠,量得 , 则的度数为( )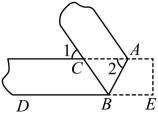 A、 B、 C、 D、8. 如图,将长方形纸片ABCD沿对角线BD折叠,点C的对应点为若 , 则的度数为( ).
A、 B、 C、 D、8. 如图,将长方形纸片ABCD沿对角线BD折叠,点C的对应点为若 , 则的度数为( ).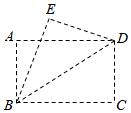 A、 B、 C、 D、9. 如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
A、 B、 C、 D、9. 如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )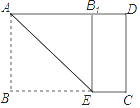 A、6cm B、4cm C、3cm D、2cm10. 下列说法不正确的是( )A、一组邻边相等的矩形是正方形 B、对角线相等的菱形是正方形 C、对角线互相垂直的矩形是正方形 D、有一个角是直角的平行四边形是正方形11. 如果正多边形的每个外角等于40°,则这个正多边形的边数是( )A、10 B、9 C、8 D、712. 如图,小明从点A出发沿直线前进10米到达点B,向左转45%后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
A、6cm B、4cm C、3cm D、2cm10. 下列说法不正确的是( )A、一组邻边相等的矩形是正方形 B、对角线相等的菱形是正方形 C、对角线互相垂直的矩形是正方形 D、有一个角是直角的平行四边形是正方形11. 如果正多边形的每个外角等于40°,则这个正多边形的边数是( )A、10 B、9 C、8 D、712. 如图,小明从点A出发沿直线前进10米到达点B,向左转45%后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )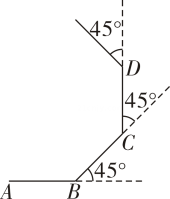 A、100米 B、80米 C、60米 D、40米13. 能说明命题“关于x的方程一定有实数根”是假命题的反例为( )A、m=1 B、m=0 C、m=4 D、m=514. 下列命题中,属于真命题的是 ( )A、两条对角线相等的四边形是矩形 B、两条对角线互相垂直的四边形是菱形 C、两条对角线互相平分的四边形是平行四边形 D、两条对角线互相垂直且相等的四边形是正方形
A、100米 B、80米 C、60米 D、40米13. 能说明命题“关于x的方程一定有实数根”是假命题的反例为( )A、m=1 B、m=0 C、m=4 D、m=514. 下列命题中,属于真命题的是 ( )A、两条对角线相等的四边形是矩形 B、两条对角线互相垂直的四边形是菱形 C、两条对角线互相平分的四边形是平行四边形 D、两条对角线互相垂直且相等的四边形是正方形二、填空题
-
15. 如图,在梯形中, , , , , , 那么梯形的周长为cm.
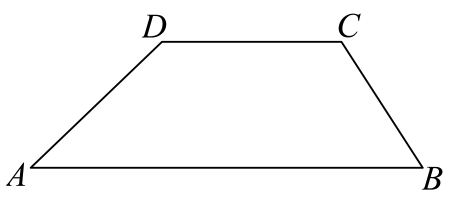 16. 如图,已知△ABC中,D,E分别是AB,AC的中点,连接DE并延长至F.使EF=DE,连接CF.若∠B=45°,则的度数为 .
16. 如图,已知△ABC中,D,E分别是AB,AC的中点,连接DE并延长至F.使EF=DE,连接CF.若∠B=45°,则的度数为 .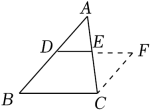 17. 如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是平行四边形,点A,B,C的坐标分别为A(0,2),B(-1,0),C(4,0),E是 BC 的中点,P 是线段AD 上的动点.若△BEP是等腰三角形,则点P 的坐标为.
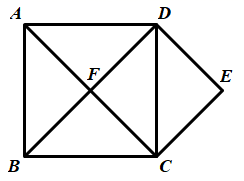
17. 如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是平行四边形,点A,B,C的坐标分别为A(0,2),B(-1,0),C(4,0),E是 BC 的中点,P 是线段AD 上的动点.若△BEP是等腰三角形,则点P 的坐标为.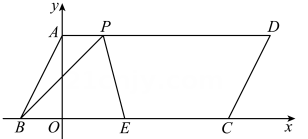 ·18. 如图,在四边形ABCD中,AC,BD相交于点O,AO=OC,BO=OD,∠ABC=90°,则四边形ABCD是;若AC=5 cm,则BD=.
·18. 如图,在四边形ABCD中,AC,BD相交于点O,AO=OC,BO=OD,∠ABC=90°,则四边形ABCD是;若AC=5 cm,则BD=.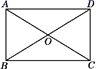 19. .如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A'重合,若 ,则 .
19. .如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A'重合,若 ,则 . 20. 如图,在Rt ABC中 , , ,D为AB的中点, ,则四边形ADCE的周长为 .
20. 如图,在Rt ABC中 , , ,D为AB的中点, ,则四边形ADCE的周长为 . 21. 如图,△ABC中,∠ACB =90°,AC=9,CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,已知DF=4,则AD的长是.
21. 如图,△ABC中,∠ACB =90°,AC=9,CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,已知DF=4,则AD的长是.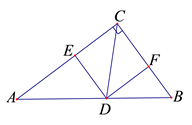 22. 如图,矩形纸片ABCD,AD=12,AB=4,点E在线段BC上,将△ECD沿DE向上翻折,点C的对应点C′落在线段AD上,点M,N分别是线段AD与线段BC上的点,将四边形ABNM沿MN向上翻折,点B恰好落在线段DE的中点B′处.则线段MN的长 .
22. 如图,矩形纸片ABCD,AD=12,AB=4,点E在线段BC上,将△ECD沿DE向上翻折,点C的对应点C′落在线段AD上,点M,N分别是线段AD与线段BC上的点,将四边形ABNM沿MN向上翻折,点B恰好落在线段DE的中点B′处.则线段MN的长 .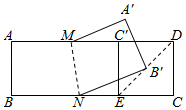
三、解答题
-
23. 如图,在四边形中, , , , ,
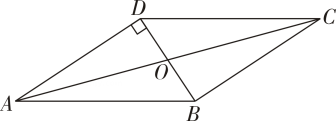 (1)、求证;四边形为平行四边形;
(1)、求证;四边形为平行四边形;
(2)、求四边形的面积.24. 如图,在▱ABCD中,AM⊥BD,CN⊥BD,垂足分别为点M,N.求证:四边形AMCN是平行四边形.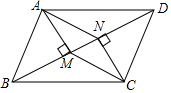 25. 如图,菱形ABCD的对角线相交于点O,BE∥AC,AE∥BD,EO与AB相交于点F.
25. 如图,菱形ABCD的对角线相交于点O,BE∥AC,AE∥BD,EO与AB相交于点F.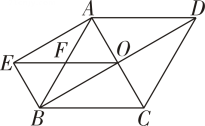 (1)、求证:EO=DC;(2)、若菱形ABCD的边长为10,∠EBA=60°,求菱形ABCD的面积.26. 如图1,将长方形纸片ABCD沿MN折叠得到图2,点A,B的对应点分别为A',B',折叠后A'M与CN相交于点E.
(1)、求证:EO=DC;(2)、若菱形ABCD的边长为10,∠EBA=60°,求菱形ABCD的面积.26. 如图1,将长方形纸片ABCD沿MN折叠得到图2,点A,B的对应点分别为A',B',折叠后A'M与CN相交于点E.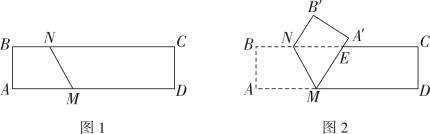 (1)、若 , 求∠A'MD的度数.(2)、设∠B'NC=α,∠A'MN=β.
(1)、若 , 求∠A'MD的度数.(2)、设∠B'NC=α,∠A'MN=β.①请用含α的代数式表示β.
②当MA'恰好平分∠DMN时,求∠A'MD的度数.
27.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE , 过点C作CF∥BE交DE的延长线于F . 求证:四边形BCFE是菱形.