【2024中考数学一轮复习】14圆基础巩固
试卷更新日期:2024-03-17 类型:一轮复习
一、选择题
-
1. 如图,线段是的直径,于点E , 若长为16,长为6,则半径是( )
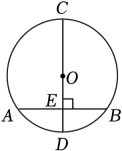 A、5 B、6 C、8 D、102. 如图所示,已知的半径为10,弦是AB上任意一点,则线段OM的长可能是( ).
A、5 B、6 C、8 D、102. 如图所示,已知的半径为10,弦是AB上任意一点,则线段OM的长可能是( ). A、5 B、7 C、9 D、113. 下列命题是假命题的是( )A、两条平行线间的距离处处相等 B、平分弦的直径垂直于弦 C、正方形的两条对角线互相垂直平分 D、在同圆或等圆中,同弧或等弧所对的圆周角相等4. 如图,在中,弦AC与半径OB交于点D , 连接OA , BC . 若 , , 则的度数为( )
A、5 B、7 C、9 D、113. 下列命题是假命题的是( )A、两条平行线间的距离处处相等 B、平分弦的直径垂直于弦 C、正方形的两条对角线互相垂直平分 D、在同圆或等圆中,同弧或等弧所对的圆周角相等4. 如图,在中,弦AC与半径OB交于点D , 连接OA , BC . 若 , , 则的度数为( )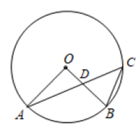 A、110° B、112° C、120° D、132°5. 如图,⊙O是△ABC的外接圆,∠A=50°,则∠BOC的度数为( )
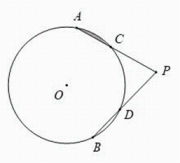
A、110° B、112° C、120° D、132°5. 如图,⊙O是△ABC的外接圆,∠A=50°,则∠BOC的度数为( ) A、40° B、50° C、80° D、100°6. 已知的半径为6cm,点到直线的距离为7cm,则直线与的位置关系是( )A、相离 B、相切 C、相交 D、无法确定7. 已知⊙O的半径为3,直线l与⊙O相交,则圆心O到直线l的距离d的取值范围是( )A、d=3 B、d>3 C、0≤d<3 D、d<38. 如图,PA、PB是⊙O的切线,A、B为切点,若∠AOB= 128 ,则∠P的度数为( )
A、40° B、50° C、80° D、100°6. 已知的半径为6cm,点到直线的距离为7cm,则直线与的位置关系是( )A、相离 B、相切 C、相交 D、无法确定7. 已知⊙O的半径为3,直线l与⊙O相交,则圆心O到直线l的距离d的取值范围是( )A、d=3 B、d>3 C、0≤d<3 D、d<38. 如图,PA、PB是⊙O的切线,A、B为切点,若∠AOB= 128 ,则∠P的度数为( )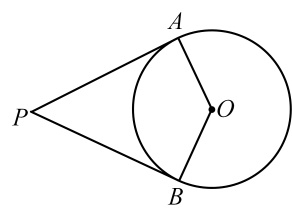 A、32° B、52° C、64° D、72°9. 如图,在Rt△ABC中,∠A=30°,BC=2 ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
A、32° B、52° C、64° D、72°9. 如图,在Rt△ABC中,∠A=30°,BC=2 ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( ) A、 ﹣ B、 ﹣ C、 ﹣ D、 ﹣10. 习近平总书记强调:“青年一代有理想、有本领、有担当,国家就有前途,民族就有希望”.如图①是一块弘扬“新时代青年励志奋斗”的扇面宣传展板,该展板的部分示意图如图②所示,它是以O为圆心, , 长分别为半径,圆心角形成的扇面,若 , , 则阴影部分的面积为( )
A、 ﹣ B、 ﹣ C、 ﹣ D、 ﹣10. 习近平总书记强调:“青年一代有理想、有本领、有担当,国家就有前途,民族就有希望”.如图①是一块弘扬“新时代青年励志奋斗”的扇面宣传展板,该展板的部分示意图如图②所示,它是以O为圆心, , 长分别为半径,圆心角形成的扇面,若 , , 则阴影部分的面积为( )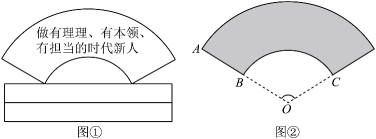 A、 B、 C、 D、11. 若扇形的圆心角为45°,半径为6,则扇形的弧长为( )A、 B、 C、 D、12. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )
A、 B、 C、 D、11. 若扇形的圆心角为45°,半径为6,则扇形的弧长为( )A、 B、 C、 D、12. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )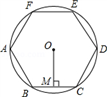 A、2, B、2 ,π C、 , D、2 ,13. 已知在半径为R的圆中,长为l的弧所对的圆心角度数为n°,则下列关系不正确的是( )A、l= B、n= C、R= D、l=2nR14. 如图,在矩形中, , 以的中点为圆心,以长为半径画弧与相切于点 , 则阴影部分的面积为( )
A、2, B、2 ,π C、 , D、2 ,13. 已知在半径为R的圆中,长为l的弧所对的圆心角度数为n°,则下列关系不正确的是( )A、l= B、n= C、R= D、l=2nR14. 如图,在矩形中, , 以的中点为圆心,以长为半径画弧与相切于点 , 则阴影部分的面积为( ) A、 B、 C、 D、15. 如图,圆锥底面圆半径为7 cm,高为24 cm,则它侧面展开图的面积为( )
A、 B、 C、 D、15. 如图,圆锥底面圆半径为7 cm,高为24 cm,则它侧面展开图的面积为( )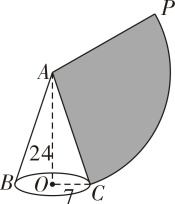 A、 B、 C、 D、16. 一个圆锥的底面半径是 ,其侧面展开图的圆心角是120°,则圆锥的母线长是( )A、 B、 C、 D、17. 若圆锥的轴截图为等边三角形,则称此圆锥为正圆锥,则正圆锥的侧面展开图的圆心角是( )A、90° B、120° C、150° D、180°
A、 B、 C、 D、16. 一个圆锥的底面半径是 ,其侧面展开图的圆心角是120°,则圆锥的母线长是( )A、 B、 C、 D、17. 若圆锥的轴截图为等边三角形,则称此圆锥为正圆锥,则正圆锥的侧面展开图的圆心角是( )A、90° B、120° C、150° D、180°二、填空题
-
18. 如图,在中,半径垂直弦于点D , 若 , , 则的长为 .
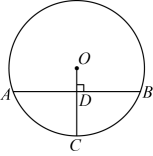 19. 如图,AB是⊙O的直径,点C在⊙O上,∠ABC=70°,PA , PC是⊙O的切线,∠P=°.
19. 如图,AB是⊙O的直径,点C在⊙O上,∠ABC=70°,PA , PC是⊙O的切线,∠P=°. 20. 如图,四边形是的内接四边形,是的直径, , 则的度数是 .
20. 如图,四边形是的内接四边形,是的直径, , 则的度数是 . 21. 如图,正五边形内接于 , 则的度数为.
21. 如图,正五边形内接于 , 则的度数为.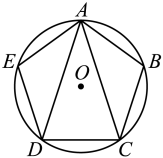 22. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若圆锥的母线长l为6cm,扇形的圆心角θ=120°,则该圆锥的侧面积为cm2.(结果保留π)
22. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若圆锥的母线长l为6cm,扇形的圆心角θ=120°,则该圆锥的侧面积为cm2.(结果保留π)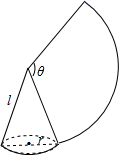 23. 已知⊙O1与⊙O2的半径分别为3和4,O1O2=7,则这两圆的位置关系为 .24.
23. 已知⊙O1与⊙O2的半径分别为3和4,O1O2=7,则这两圆的位置关系为 .24.圆和圆有不同的位置关系.与下图不同的圆和圆的位置关系是 .(只填一种)

三、解答题
-
25. 如图,OA=OB,AB交⊙O于点C,D,OE是半径,且OE⊥AB于点F.
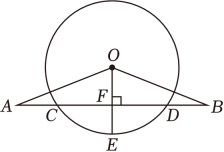 (1)、求证:AC=BD .(2)、若CD=4,EF=1,求⊙O的半径.26. 如图,在中, . 延长到O , 使 , 以O 为圆心,长为半径作交延长线于点D , 连结 .
(1)、求证:AC=BD .(2)、若CD=4,EF=1,求⊙O的半径.26. 如图,在中, . 延长到O , 使 , 以O 为圆心,长为半径作交延长线于点D , 连结 . (1)、求扇形的面积.(2)、判断所在直线与的位置关系,并说明理由.27. 如图,是的直径,点在的延长线上, , , 交的延长线于点 .
(1)、求扇形的面积.(2)、判断所在直线与的位置关系,并说明理由.27. 如图,是的直径,点在的延长线上, , , 交的延长线于点 .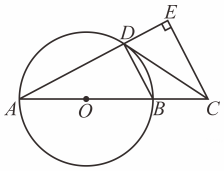 (1)、求证:与相切:(2)、若 , , 求的长.28. 如图,在⊙O中,AB是直径,C是圆上一点.在AB的延长线上取一点D,连结CD,使∠BCD=∠A.
(1)、求证:与相切:(2)、若 , , 求的长.28. 如图,在⊙O中,AB是直径,C是圆上一点.在AB的延长线上取一点D,连结CD,使∠BCD=∠A. (1)、求证:直线CD是⊙O的切线.(2)、若∠ACD=120°,CD=2 , 求图中阴影部分的面积.
(1)、求证:直线CD是⊙O的切线.(2)、若∠ACD=120°,CD=2 , 求图中阴影部分的面积.