【2024中考数学一轮复习】15尺规作图、视图、投影基础巩固
试卷更新日期:2024-03-17 类型:一轮复习
一、选择题
-
1. 如图,下列四种用无刻度直尺和圆规作角平分线的方法,其中不正确的个数是( )
 A、个 B、个 C、个 D、个2. 如图是某个几何体的展开图,该几何体是( )
A、个 B、个 C、个 D、个2. 如图是某个几何体的展开图,该几何体是( )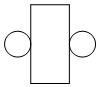 A、圆锥 B、圆柱 C、圆台 D、四棱柱3. 如图是一个几何体的平面展开图,则这个几何体是( )
A、圆锥 B、圆柱 C、圆台 D、四棱柱3. 如图是一个几何体的平面展开图,则这个几何体是( )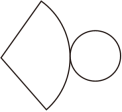 A、
A、 B、
B、 C、
C、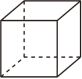 D、
D、 4. 如图是某个几何体的平面展开图,该几何体是( )
4. 如图是某个几何体的平面展开图,该几何体是( )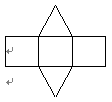 A、
A、 B、
B、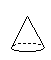 C、
C、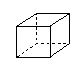 D、
D、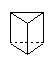 5. 下列图形属于棱锥侧面展开图的是( )A、
5. 下列图形属于棱锥侧面展开图的是( )A、 B、
B、 C、
C、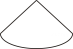 D、
D、 6. 如图,这是一个几何体的侧面展开图,则该几何体的形状是( )
6. 如图,这是一个几何体的侧面展开图,则该几何体的形状是( )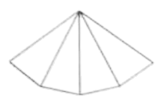 A、四棱柱 B、四棱锥 C、五棱柱 D、五棱锥7. 如图,已知钝角 ,依下列步骤尺规作图,并保留了作图痕迹.
A、四棱柱 B、四棱锥 C、五棱柱 D、五棱锥7. 如图,已知钝角 ,依下列步骤尺规作图,并保留了作图痕迹.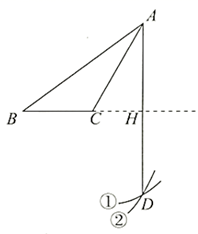
步骤1:以 为圆心, 长为半径画弧①;
步骤2:以 为圆心, 长为半径画弧②,交弧①于点 ;
步骤3:连接 ,交 的延长线于点 .
则下列说法错误的是( )
A、 是 中 边上的高 B、 C、 平分 D、作图依据是:①两点确定一条直线;②到线段两端点距离相等的点在线段的垂直平分线上8. 如图所示均为几何体的展开图,则从左到右的图形对应的几何体分别为( ) A、圆锥、三棱锥、圆柱、正方体 B、圆锥、四棱锥、圆柱、正方体 C、圆锥、四棱柱、圆柱、正方体 D、圆锥、三棱柱、圆柱、正方体9. 下列几何体中,其侧面展开图为扇形的是( )A、
A、圆锥、三棱锥、圆柱、正方体 B、圆锥、四棱锥、圆柱、正方体 C、圆锥、四棱柱、圆柱、正方体 D、圆锥、三棱柱、圆柱、正方体9. 下列几何体中,其侧面展开图为扇形的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图是某个几何体的展开图,则这个几何体是( )
10. 如图是某个几何体的展开图,则这个几何体是( )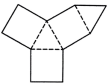 A、圆柱 B、正方体 C、长方体 D、三棱柱11. 如图是某几何体的展开图,该几何体是( )
A、圆柱 B、正方体 C、长方体 D、三棱柱11. 如图是某几何体的展开图,该几何体是( ) A、长方体 B、圆柱 C、圆锥 D、三棱柱12. 小明用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有( )
A、长方体 B、圆柱 C、圆锥 D、三棱柱12. 小明用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有( )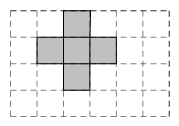 A、1种 B、2种 C、3种 D、4种13. 把图中三棱柱沿表面展开,所得到的平面图形可以是( )
A、1种 B、2种 C、3种 D、4种13. 把图中三棱柱沿表面展开,所得到的平面图形可以是( ) A、
A、 B、
B、 C、
C、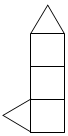 D、
D、 14. 由下面正方体的平面展开图可知,原正方体“我”字所在面的对面的汉字是( )
14. 由下面正方体的平面展开图可知,原正方体“我”字所在面的对面的汉字是( ) A、国 B、的 C、中 D、梦15. 下列图形中,能够折叠成一个正方体的是( )A、
A、国 B、的 C、中 D、梦15. 下列图形中,能够折叠成一个正方体的是( )A、 B、
B、 C、
C、 D、
D、 16. 正方体的六个面上分别标有1,2,3,4,5,6六个数字,下图是三种不同的放置方式,与数字“2”相对的面上的数字是( )
16. 正方体的六个面上分别标有1,2,3,4,5,6六个数字,下图是三种不同的放置方式,与数字“2”相对的面上的数字是( ) A、1 B、3 C、4 D、517. 如图,是一个棱长为1的正方体纸盒.若一只蚂蚁要沿着正方体纸盒的表面,从顶点 爬到顶点 去觅食,则需要爬行的最短路程是( )
A、1 B、3 C、4 D、517. 如图,是一个棱长为1的正方体纸盒.若一只蚂蚁要沿着正方体纸盒的表面,从顶点 爬到顶点 去觅食,则需要爬行的最短路程是( ) A、 B、2 C、 D、318. 一个正方体的展开图如图所示,如果正方体相对的两个面所标的数字均互为相反数,那么的值为( )
A、 B、2 C、 D、318. 一个正方体的展开图如图所示,如果正方体相对的两个面所标的数字均互为相反数,那么的值为( )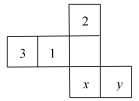 A、 B、 C、 D、19. 在下面的图形中,不是正方体的展开图的是( )A、
A、 B、 C、 D、19. 在下面的图形中,不是正方体的展开图的是( )A、 B、
B、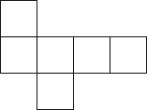 C、
C、 D、
D、
二、填空题
-
20. 如图,已知线段 ,其垂直平分线 的作法如下:①分别以点 和点 为圆心, 长为半径画弧,两弧相交于 , 两点;②作直线 .上述作法中 满足的条作为 1.(填“ ”,“ ”或“ ”)
 21. 如图,是一个正方体纸盒的展开图,若在其中两个正方形 , 内分别填上适当的数,使得折叠成正方体后相对面上的两个数互为相反数,则正方形内填入的数是 .
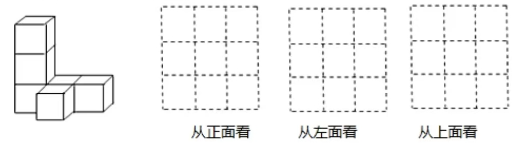
21. 如图,是一个正方体纸盒的展开图,若在其中两个正方形 , 内分别填上适当的数,使得折叠成正方体后相对面上的两个数互为相反数,则正方形内填入的数是 . 22. 棱长为2的正方体,摆成如图所示的形状,则该物体的表面积是 .
22. 棱长为2的正方体,摆成如图所示的形状,则该物体的表面积是 . 23. 种树时,只要定出两个树坑的位置,就能使同一行树坑在同一条直线上,其中的数学道理是 .24. 如图,从教学楼到图书馆总有少数同学不走人行道而横穿草坪,虽然明知不对,可他们还是要这样做,请用我们所学的数学知识解释这一现象: .
23. 种树时,只要定出两个树坑的位置,就能使同一行树坑在同一条直线上,其中的数学道理是 .24. 如图,从教学楼到图书馆总有少数同学不走人行道而横穿草坪,虽然明知不对,可他们还是要这样做,请用我们所学的数学知识解释这一现象: .
三、解答题
-
25. 图中的直线l表示一条小河,点A,B表示两个、村庄.在何处架桥才能使A村到B村的路程最短?
 26. 如图是一个正方体纸盒的表面展开图,纸盒中相对两个面上的数互为倒数.
26. 如图是一个正方体纸盒的表面展开图,纸盒中相对两个面上的数互为倒数.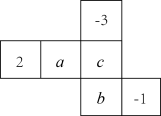 (1)、填空: , ;(2)、先化简,再求值: .27. 如图,是的平分线,是的平分线, .
(1)、填空: , ;(2)、先化简,再求值: .27. 如图,是的平分线,是的平分线, . (1)、求的度数;(2)、若 , 求的度数.28. 已知是直线上的一点,是直角,平分 , 如图(1)所示.
(1)、求的度数;(2)、若 , 求的度数.28. 已知是直线上的一点,是直角,平分 , 如图(1)所示.
 (1)、①若 , 求的度数;
(1)、①若 , 求的度数;②若 , 直接写出的度数(用含的式子表示).
(2)、将图(1)中的绕点顺时针旋转至图(2)所示的位置,试探究和的度数之间的关系,写出你的结论,并说明理由.