【2024中考数学一轮复习】17图形的相似基础巩固
试卷更新日期:2024-03-17 类型:一轮复习
一、选择题
-
1. 若 , 则的值为( )A、1 B、 C、 D、2. 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=2,BC=4,EF=3,则DE的长为 ( )
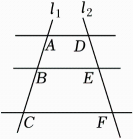 A、1 B、1.5 C、2 D、2.53. 如图,在 中, , , , ,则 的长为( )
A、1 B、1.5 C、2 D、2.53. 如图,在 中, , , , ,则 的长为( )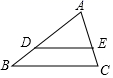 A、 B、 C、 D、4. 如图,已知 , , 若的长度为6,则的长度为( )
A、 B、 C、 D、4. 如图,已知 , , 若的长度为6,则的长度为( ) A、4 B、9 C、12 D、5. 已知△ABC与△A'B'C'是位似图形,位似比是1:3,则△ABC与△A'B'C'的面积比是( )A、1:3 B、1:6 C、1:9 D、3:16. 如图,在中,点D、E分别是边BC、AC上的点,连接DE,若 , 且 , , 则的值是( ).
A、4 B、9 C、12 D、5. 已知△ABC与△A'B'C'是位似图形,位似比是1:3,则△ABC与△A'B'C'的面积比是( )A、1:3 B、1:6 C、1:9 D、3:16. 如图,在中,点D、E分别是边BC、AC上的点,连接DE,若 , 且 , , 则的值是( ).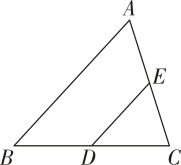 A、 B、 C、 D、7. 如图,在中,是边上的点, , :: , 则与的面积比是( )
A、 B、 C、 D、7. 如图,在中,是边上的点, , :: , 则与的面积比是( )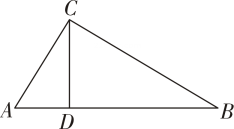 A、:
A、:
B、:
C、:
D、:8. 如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,并测得 , , 那么树DB的高度是( )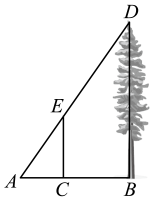 A、6m B、8m C、32m D、25m9. 如图,在 中,已知 ,则下列等式成立的是
A、6m B、8m C、32m D、25m9. 如图,在 中,已知 ,则下列等式成立的是 A、 B、 C、 D、10. 如图,已知 , 那么添加下列一个条件后,不能判定的是( )
A、 B、 C、 D、10. 如图,已知 , 那么添加下列一个条件后,不能判定的是( ) A、 B、 C、 D、11. 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
A、 B、 C、 D、11. 如图,要使△ACD∽△ABC,需要补充的一个条件是( )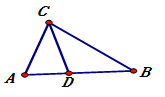 A、 B、 C、 D、12. 如图,小明同学利用相似三角形测量旗杆的高度,若测得木杆AB长2m,它的影长BC为1m,旗杆DE的影长EF为6m,则旗杆DE的高度为( )
A、 B、 C、 D、12. 如图,小明同学利用相似三角形测量旗杆的高度,若测得木杆AB长2m,它的影长BC为1m,旗杆DE的影长EF为6m,则旗杆DE的高度为( )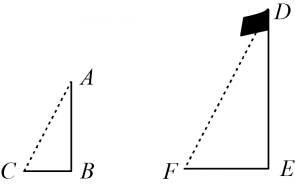 A、9m B、10m C、11m D、12m13. 如图,四边形和相似,则和的大小分别为( )
A、9m B、10m C、11m D、12m13. 如图,四边形和相似,则和的大小分别为( ) A、 30 B、 33 C、 30 D、 3314. 如图,取一张长为 、宽为 的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边 应满足的条件是( )
A、 30 B、 33 C、 30 D、 3314. 如图,取一张长为 、宽为 的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边 应满足的条件是( ) A、 B、 C、 D、15. 如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A'的坐标是( )
A、 B、 C、 D、15. 如图,在平面直角坐标系中,已知点A(2,2),B(4,1),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A'的坐标是( )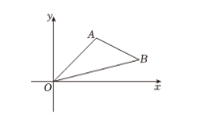 A、(1,1) B、(4,4)或(8,2) C、(4,4) D、(4,4)或(-4,-4)
A、(1,1) B、(4,4)或(8,2) C、(4,4) D、(4,4)或(-4,-4)二、填空题
-
16. 已知△ABC∽△A′B′C′,相似比为3:4,△ABC的周长为6,则△A′B′C′的周长为 .17. 如果两个相似三角形的面积之比为 , 那么这两个三角形一组对边上的中线之比为 .18. 已知 , , , 的高为6,那么的高长为 .19. 如图,在平行四边形中,是线段上一点,连结、交于点.若 , 则.
 20. 如图,在△ABC中,∠AED=∠B,若AB=10,AE=8,DE=6,则BC的长为.
20. 如图,在△ABC中,∠AED=∠B,若AB=10,AE=8,DE=6,则BC的长为. 21. 如图是小孔成像原理示意图,若点O到AB的距离是18cm,O到CD的距离是6cm,物体AB的高度是9cm,则像CD的高度是cm.
21. 如图是小孔成像原理示意图,若点O到AB的距离是18cm,O到CD的距离是6cm,物体AB的高度是9cm,则像CD的高度是cm.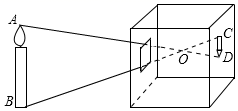 22. 在某一时刻测得一根高为1.8m的竹竿的影长为3m,同时同地测得一栋楼的影长为90m,则这栋楼的高度为m.23. 如图,A,B两点分别位于一个池塘的两端,为了测量A、B之间的距离,小天想了一个办法:在地上取一点C,使它可以直接到达A、B两点,连接AC,BC,在AC上取一点M,使AM=3MC,作MN//AB交BC于点N,测得MN=36m,则A、B两点间的距离为.
22. 在某一时刻测得一根高为1.8m的竹竿的影长为3m,同时同地测得一栋楼的影长为90m,则这栋楼的高度为m.23. 如图,A,B两点分别位于一个池塘的两端,为了测量A、B之间的距离,小天想了一个办法:在地上取一点C,使它可以直接到达A、B两点,连接AC,BC,在AC上取一点M,使AM=3MC,作MN//AB交BC于点N,测得MN=36m,则A、B两点间的距离为. 24. 如图,在平面直角坐标系中,△ABC与△A'B'C是位似图形,位似中心是原点O,已知点A (2,a)、A' (4,b),则△ABC与△A' B' C'的相似比是
24. 如图,在平面直角坐标系中,△ABC与△A'B'C是位似图形,位似中心是原点O,已知点A (2,a)、A' (4,b),则△ABC与△A' B' C'的相似比是 25. 如图,的顶点坐标是 , , , 以点O为位似中心,将缩小为原来的 , 得到 , 则点的坐标为.
25. 如图,的顶点坐标是 , , , 以点O为位似中心,将缩小为原来的 , 得到 , 则点的坐标为.
三、解答题
-
26. 如图,△ABC∽△ACD .
 (1)、若CD平分∠ACB , ∠ACD=40° , 求∠ADC的度数.(2)、若AD=2,BD=3,求AC的长.27. 如图, ,直线 , 与这三条平行线分别交于点 , , 和点 , , ,已知 , , ,则 的长为?
(1)、若CD平分∠ACB , ∠ACD=40° , 求∠ADC的度数.(2)、若AD=2,BD=3,求AC的长.27. 如图, ,直线 , 与这三条平行线分别交于点 , , 和点 , , ,已知 , , ,则 的长为?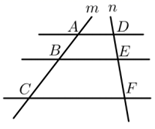 28. 如图,矩形中, , 点M是的中点,连接 . 将沿着折叠后得 , 延长交于E , 连接 .
28. 如图,矩形中, , 点M是的中点,连接 . 将沿着折叠后得 , 延长交于E , 连接 . (1)、求证:平分;(2)、求证:△EMC∽△MAB.29. 学习了相似三角形知识后,小丽同学准备用自制的直角三角形纸板测量校园内一棵古树的高度.已知三角形纸板的斜边长为0.5米,较短的直角边长为0.3米.
(1)、求证:平分;(2)、求证:△EMC∽△MAB.29. 学习了相似三角形知识后,小丽同学准备用自制的直角三角形纸板测量校园内一棵古树的高度.已知三角形纸板的斜边长为0.5米,较短的直角边长为0.3米. (1)、小丽先调整自己的位置至点P,将直角三角形纸板的三个顶点位置记为A、B、C(如图①),斜边AB平行于地面MN(点M、P、E、N在一直线上),且点D在边AC(较长直角边)的延长线上,此时测得边AB距离地面的高度EF为1.5米,小丽与古树的距离AF为16米,求古树的高度DE;(2)、为了尝试不同的思路,小丽又向前移动自己的位置至点Q,将直角三角形纸板的三个顶点的新位置记为A′、B′、C′(如图②),使直角边B′C′(较短直角边)平行于地面MN(点M、Q、E、N在一直线上),点D在斜边B′A′的延长线上,且测得此时边B′C′距离地面的高度依然是1.5米,那么小丽向前移动了多少米?30.
(1)、小丽先调整自己的位置至点P,将直角三角形纸板的三个顶点位置记为A、B、C(如图①),斜边AB平行于地面MN(点M、P、E、N在一直线上),且点D在边AC(较长直角边)的延长线上,此时测得边AB距离地面的高度EF为1.5米,小丽与古树的距离AF为16米,求古树的高度DE;(2)、为了尝试不同的思路,小丽又向前移动自己的位置至点Q,将直角三角形纸板的三个顶点的新位置记为A′、B′、C′(如图②),使直角边B′C′(较短直角边)平行于地面MN(点M、Q、E、N在一直线上),点D在斜边B′A′的延长线上,且测得此时边B′C′距离地面的高度依然是1.5米,那么小丽向前移动了多少米?30.如图所示的网格中,每个小方格都是边长为1的小正方形,B(﹣1,﹣1),C(5,﹣1)
 (1)、把△ABC绕点C按顺时针旋转90°后得到△A1B1C1 , 请画出这个三角形并写出点B1的坐标;(2)、以点A为位似中心放大△ABC,得到△A2B2C2 , 使放大前后的面积之比为1:4,请在下面网格内出△A2B2C2 .
(1)、把△ABC绕点C按顺时针旋转90°后得到△A1B1C1 , 请画出这个三角形并写出点B1的坐标;(2)、以点A为位似中心放大△ABC,得到△A2B2C2 , 使放大前后的面积之比为1:4,请在下面网格内出△A2B2C2 .