【2024中考数学一轮复习】18统计与概率基础巩固

试卷更新日期：2024-03-16 类型：一轮复习

进入出卷网下载

一、选择题

1. 下列调查方式中，适合的是（）

A、《新闻联播》电视栏目的收视率，采用普查方式 B、某小型企业给在职员工做工作服前进行尺寸大小调查，采用抽样调查方式 C、一批灯泡的使用寿命，采用普查方式 D、环保部门对安乡珊泊湖水质情况的调查，采用抽样调查方式

查看试题解析
2. 某校举办“强国复兴有我，争做新时代美德少年”演讲比赛．比赛中，九位评委给某个选手打分，如果去掉一个最高分和一个最低分，则下列数据一定不发生变化的是（）

A、方差 B、平均数 C、众数 D、中位数

查看试题解析
3. 下表是浙江省七个城市某季度 GDP(地区生产总值)数据的情况：
城市
嘉兴
绍兴
温州
衢州
杭州
宁波
台州
GDP(亿元)
1517
1610
1889
437
4539
3516
1375
则这组数据的中位数是（）

A、1 889 亿元 B、1610 亿元 C、1517 亿元 D、437亿元

查看试题解析
4. 小楠所在社会实践活动小组的同学们响应“垃圾分类，从我做起”的号召，主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示，那么这组数据的众数和中位数分别是（）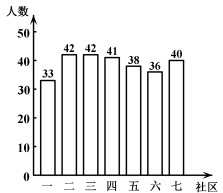

A、42，40 B、42，38 C、2，40 D、2，38

查看试题解析
5. 在射击训练中，某队员的10次射击成绩如图，则这10次射击成绩的中位数(单位：环)和众数(单位：环)分别是（）

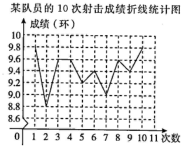A、9.6，9.6 B、9.5，9.4 C、9.5，9.6 D、9.6，9.8

查看试题解析
6. 为了了解2015年我县九年级学生学业水平考试的数学成绩，从中随机抽取了1000名学生的数学成绩，下列说法正确的是（　　）

A、2015年我县九年级学生是总体 B、样本容量是1000 C、1000名九年级学生是总体的一个样本 D、每一名九年级学生是个体

查看试题解析
7. 为了解某校学生每周参加社团活动时间的情况，随机抽查了100名学生的社团活动时间进行统计，并绘制成如图所示的频数分布直方图，已知该校共有1200名学生，依此估计，该校每周参加社团活动的时间在6～8小时之间的学生数大约是（）

A、240名 B、300名 C、360名 D、480名

查看试题解析
8. 在某次考试中，某班级的数学成绩统计图如图所示，下列说法中错误的是（）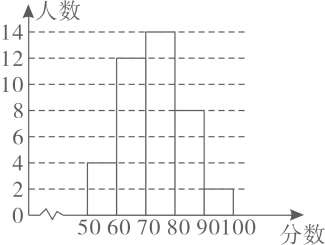

A、得分在70~80分之间的人数最多 B、该班总人数为40人 C、得分在90~100分之间的人数最少 D、不低于60分为及格，该班的及格率为80%

查看试题解析
9. 某校组织了第二课堂，分别设置了文艺类，体育类、阅读类、兴趣类四个社团（假设该校要求人人参与社团，每人只能选择一个），为了了解学生喜爱哪种社团活动，学校做了一次抽样调查，并绘制成如图①，图②所示的两幅不完整的统计图，根据图中信息回答，下列结论正确的是（）

A、本次抽样调查的样本容量是50 B、阅读类对应扇形的圆心角是 $90 °$ C、样本中喜爱体育类社团的有16人 D、若全校有800名学生，则喜爱文艺类社团的有200人

查看试题解析
10. 下列事件是必然事件的为（）

A、明天早上会下雨 B、任意一个三角形，它的内角和等于180° C、掷一枚硬币，正面朝上 D、打开电视机，正在播放“瑞安新闻”

查看试题解析
11. 从数学的观点看，对以下成语及诗句中的事件判断正确的是（）

A、成语“守株待兔”是随机事件 B、成语“水中捞月”是随机事件 C、诗句“清明时节雨纷纷”是必然事件 D、诗句“离离原上草，一岁一枯荣”是不可能事件

查看试题解析
12. 下列事件中，属于必然事件的是（）

A、明天会下雨 B、抛一枚硬币，正面朝上 C、地球每天都在自转 D、打开电视机，正在播放广告

查看试题解析
13. 为了更好地落实“双减”政策，学校设置了以实践探究为主的个性化作业，如图是某学生设计的电路图，随机闭合开关 $S_{1}$ ， $S_{2}$ ， $S_{3}$ 中的两个，能让灯泡发光的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析

二、填空题

14. 为了了解十一黄金周某汽车站的客流量，现随机抽取了其中3天的客流量展开调查，在这次调查中，采用的调查方式是.其中，总体是，个体是，样本是，样本容量是.

查看试题解析
15. 小云和小天练习射击，一轮10发子弹打完后，两人的成绩如图所示.根据图中的信息，小云和小天两人中成绩较稳定的是.

查看试题解析
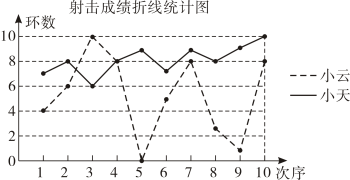16. 若一组数据1，3，x，5，4，6的平均数是4，则这组数据的中位数是.

查看试题解析
17. 随着体育中考的临近，某校随机调查了 45名学生的跳远成绩，结果如下表所示：
跳远成绩(cm)
160
170
180
190
200
210
人数
3
9
6
9
15
3
则这些同学的跳远成绩的众数为cm，中位数为cm

查看试题解析
18. 某射击运动员封闭训练 $10$ 个月，每天击中 $9$ 环以上的频率记录如图，封闭训练结束时，估计这名运动员射击一次时“击中 $9$ 环以上”的概率为 $($ 结果保留一位小数 $)$ ．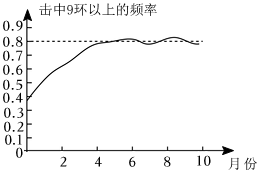

查看试题解析
19. 任意抛掷一只纸杯200次，经过统计发现“杯口朝上”的次数为48次，则由此可以估计这只纸杯出现“杯口朝上”的概率为．

查看试题解析
20. 垃圾分类是指按照垃圾的不同成分，属性、利用价值以及对环境的影响，并根据不同处置方式的要求，分成属性不同的若干种类.某市试点区域的垃圾收集情况如扇形统计图所示，已知可回收垃圾共收集60吨，且全市人口约为试点区域人口的10倍，那么估计全市可收集的干垃圾总量为吨.

查看试题解析
21. 从 $\sqrt{16}$ ， $\frac{22}{7}$ ， $\sqrt{2}$ ， $π$ 四个实数，任取一个数是有理数的概率为．

查看试题解析
22. 如图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，且分别标有数字，分别转动两个转盘一次，转盘停止时（若指针恰好停在分割线上，那么重转一次，直到指针指向某一区域为止），则两个指针所指区域的数字之积为偶数的概率是．

查看试题解析

三、解答题

23. 某校在七年级（1）班学生中开展对于“我国国家公祭日”知晓情况的问卷调查．问卷调查的结果分为A、B、C、D四类，其中A类表示“非常了解”；B类表示“比较了解”；C类表示“基本了解”；D类表示“不太了解”；班长将本班同学的调查结果绘制成下列两幅不完整的统计图．请根据上述信息解答下列问题：

(1)、该班参与问卷调查的人数有人；

(2)、求C类人数占总调查人数的百分比；

(3)、求扇形统计图中A类所对应扇形圆心角的度数．

查看试题解析
24. 为促进师生身心全面健康发展，进一步推广“阳光体育”大课间活动，某学校就学生对 $A$ 实心球， $B$ 立定跳远， $C$ 跑步， $D$ 跳绳四种体育活动项目喜欢情况进行调查，随机抽取了部分学生，并将调查结果绘制成图 $1$ ，图 $2$ 的统计图，请结合图中的信息解答下列问题：

(1)、请计算本次被调查的学生总人数和喜欢“跑步”的学生人数；

(2)、将两个统计图补充完整；

(3)、随机抽取了 $4$ 名喜欢“跑步”的学生，其中有 $2$ 名女生， $2$ 名男生，现从这 $4$ 名学生中任意抽取 $2$ 名学生，请用画树状图或列表的方法，求出刚好抽到 $2$ 名女生的概率．

查看试题解析
25. 为了解某校八年级学生立定跳远水平，随机抽取该年级 $50$ 名学生进行测试，并把测试成绩（单位： $m$ ）绘制成不完整的频数分布表和频数分布直方图．
分组
频数
          $1.2 \leq x < 1.6$
          $8$
          $1.6 \leq x < 2.0$
          $12$
          $2.0 \leq x < 2.4$
          $2.4 \leq x < 2.8$
          $10$
请根据图表中所提供的信息，完成下列问题：

(1)、请把频数分布直方图补充完整；

(2)、跳远成绩大于等于 $2.0 m$ 为优秀，若该校八年级共有 $1300$ 名学生，估计该年级学生立定跳远成绩优秀的学生有多少人？

查看试题解析
26. 在一个不透明的口袋中装有4张相同的纸牌，它们分别标有数字1，2，3，4，随机地摸取两张纸牌，请用列表或画树状图的方法解决下列问题．

(1)、计算摸取的两张纸牌上数字之和为5的概率；

(2)、甲、乙两人进行游戏，如果摸取的两张纸牌上数字之和为奇数，则甲胜；如果摸取的两张纸牌上数字之和为偶数，则乙胜．这个游戏公平吗？请说明理由．

查看试题解析
27. 从分别标有1~10号的10张卡片中抽取1张，已知下列事件：
①号码是偶数，②号码是奇数，③号码是5，④号码既是2的倍数，又是3的倍数，⑤号码既是5的倍数，又是3的倍数，⑥号码大于4．

(1)、上述事件中有没有必然发生的事件？

(2)、有没有不可能发生的事件？

(3)、哪一个事件出现的可能性最大？

(4)、哪一个事件出现的可能性最小？

(5)、有没有可能性一样大的事件？

查看试题解析
28. 为了打造书香文化，培养阅读习惯．崇德中学计划在各班建图书角，开展“我最喜欢的书籍”为主题的调查活动，学生根据自己的爱好选择一类书籍（A：科技类，B：文学类，C：政史类，D：艺术类，E：其他类）．张老师组织数学兴趣小组对学校部分学生进行了问卷调查，根据收集到的数据，绘制了两幅不完整的统计图（如图所示）．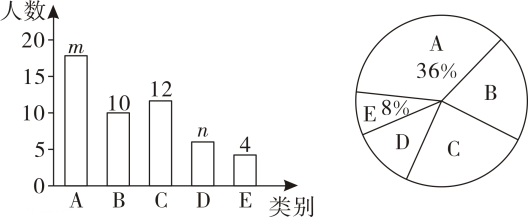
根据图中信息，请回答下列问题；

(1)、条形图中的m＝， n＝，

(2)、文学类书籍对应扇形圆心角等于度：

(3)、若该校有2000名学生，请你估计最喜欢阅读政史类书籍的学生人数；

(4)、甲同学从A，B，C三类书籍中随机选择一种，乙同学从B，C，D三类书籍中随机选择一种，请用画树状图或者列表法求甲乙两位同学选择相同类别书籍的概率．

查看试题解析

城市	嘉兴	绍兴	温州	衢州	杭州	宁波	台州
GDP(亿元)	1517	1610	1889	437	4539	3516	1375

分组	频数
$1.2 \leq x < 1.6$	$8$
$1.6 \leq x < 2.0$	$12$
$2.0 \leq x < 2.4$
$2.4 \leq x < 2.8$	$10$

跳远成绩(cm)	160	170	180	190	200	210
人数	3	9	6	9	15	3