【2024中考数学一轮复习】19规律探索问题基础巩固

试卷更新日期：2024-03-16 类型：一轮复习

进入出卷网下载

一、填空题

1. 观察这列数0，-1，2，-3，4，则这组数据的第2023个数为．

查看试题解析
2. 将一列自然数按如图所示的规律排列， $A_{1}$ 表示的数为1， $A_{2}$ 表示的数为10， $A_{10}$ 表示的数为．

查看试题解析
3. 小苗探究了一道有关分式的规律题， $\frac{1}{x + 3}$ ， $\frac{3}{x + 5}$ ， $\frac{4}{x + 7}$ ， $\frac{7}{x + 9}$ ， $\frac{11}{x + 11}$ ，， $\frac{29}{x + 15}$ ， …请按照此规律在横线上补写出第6个分式．

查看试题解析
4. 下表在我国宋朝数学家杨辉1261年的著作《解：九章算法》中提到过，因而人们把这个表叫做杨辉三角，请你根据杨辉三角的规律补全下表第四行空缺的数字是.

查看试题解析
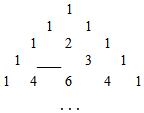5. 按一定规律排列的一列数依次为 $\frac{1}{2}$ ， $- \frac{1}{5}$ ， $\frac{1}{10}$ ， $- \frac{1}{17}$ ， $\frac{1}{26}$ ， $- \frac{1}{37}$ ，…，按此规律排列下去，这列数中第8个数是，第 $n$ 个数是（ $n$ 为正整数）．

查看试题解析
6. 观察下列有规律的等式：① $\sqrt{1 - \frac{1}{2}} = \sqrt{\frac{1}{2}}$ ；② $\sqrt{2 - \frac{2}{5}} = 2 \sqrt{\frac{2}{5}}$ ；③ $\sqrt{3 - \frac{3}{10}} = 3 \sqrt{\frac{3}{10}}$ ；…….则第6个等式为.

查看试题解析
7. （阅读材料）“九宫图”源于我国古代夏禹时期的“洛书” $($ 图1所示 $)$ ，是世界上最早的矩阵，又称“幻方”，用今天的数学符号翻译出来，“洛书”就是一个三阶“幻方” $($ 图2所示 $)$ ．
（规律总结）观察图1、图2，根据“九宫图”中各数字之间的关系，我们可以总结出“幻方”需要满足的条件是；若图3，是一个“幻方”，则 $a =$ ．

查看试题解析
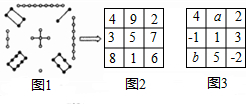8.
如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P₁（0，1），P₂（1，1），P₃（1，0），P₄（1，﹣1），P₅（2，﹣1），P₆（2，0），…，则点P₆₀的坐标是．

查看试题解析
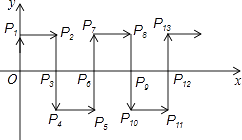9. 填在下面各正方形中的四个数之间都有相同的规律，根据此规律，m的值是．

查看试题解析
10. 如图是一个三角形点阵，从上向下数有无数多行，其中第1行有1个点，第2行有2个点，⋯，第n行有n个点，容易发现，三角形点阵中前4行的点数和为10.若三角形点阵中前a行的点数和为300，则a的值为.

查看试题解析
11. 每一个多边形都可分割（分割方法如图）成若干个三角形．根据这种方法八边形可以分割成个三角形．用此方法n边形能割成个三角形．

查看试题解析
12. 观察下列图形：它们是按一定规律排列的，依照此规律，第2021个图形中共有个五角星．

查看试题解析
13. 如图是一组有规律的图案，图案（1）是由4个组成的，图案（2）是由7个组成的，那么图案（3）是由个组成的．

查看试题解析
14. 如图是平面直角坐标系中的一组直线，按此规律推断，第5条直线与x轴交点的横坐标是.

查看试题解析
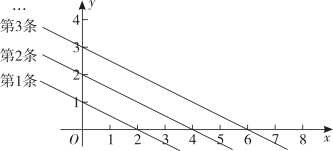15. 如图，平面内有公共端点的六条射线OA，OB，OC，OD，OE，OF，从射线OA开始按逆时针方向依次在射线上写出数字1、2、3、4、5、6、7…，则数字“2016”在射线上．

查看试题解析
16. 把一根起点为0的数轴弯折成如图所示的样子，虚线最下面第1个数字是0，往上第2个数字是6，第3个数字是21，…，则第23个数字是．

查看试题解析
17. 如图，在平面直角坐标系中，点A₁ ， A₂ ， A₃ ， …都在x轴上，点B₁ ， B₂ ， B₃ ， …都在直线y＝x上，OA₁＝1，且△B₁A₁A₂ ， B₂A₂A₃ ， B₃A₃A₄ ， …，△B_nA_nA_n+1 ， …分别是以A₁ ， A₂ ， A₃ ， …，A_n ， …为直角顶点的等腰直角三角形，则△B₁₀A₁₀A₁₁的面积是．

查看试题解析
18. 正方形 $A_{1} B_{1} C_{1} O$ ， $A_{2} B_{2} C_{2} C_{1}$ ， $A_{3} B_{3} C_{3} C_{2}$ ， …按如图的方式放置，点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， …和点 $C_{1}$ ， $C_{2}$ ， $C_{3}$ ， …分别在直线 $y = x + 1$ 和 $x$ 轴上，则点 $B_{2023}$ 的坐标为．

查看试题解析

二、选择题

19. 按一定规律排列的单项式：a，a² ， a³ ， a⁴ ， a⁵ ， …，则第n个单项式是（）

A、aⁿ⁺¹ B、aⁿ C、a^n-1 D、a²ⁿ

查看试题解析
20. 如图是一个运算程序的示意图，若开始输入x的值为18，则第10次输出的结果为（）

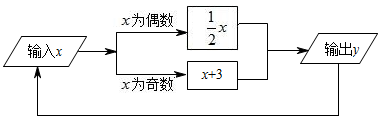A、5 B、0 C、3 D、6

查看试题解析
21. 生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型.在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2ⁿ来表示.即：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，……，请你推算2²⁰²²的个位数字是（）

A、8 B、6 C、4 D、2

查看试题解析
22. 观察下列关于x的单项式： $x$ ， $- 3 x^{2}$ ， $5 x^{3}$ ， $- 7 x^{4}$ ， …按照上述规律，则第2022个单项式是（）

A、 $4045 x^{2022}$ B、 $- 4045 x^{2022}$ C、 $4043 x^{2022}$ D、 $- 4043 x^{2022}$

查看试题解析
23. 观察下列按一定规律排列的n个数：2，4，6，8，10，12，…；若最后三个数之和是3000，则n等于（）

A、499 B、500 C、501 D、1002

查看试题解析
24. 如图，下列各图形中的三个数之间均具有相同的规律．根据此规律，图形中M与m，n的关系是（）

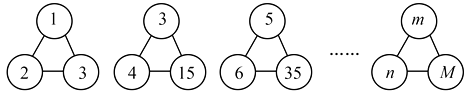A、M＝mn B、M＝n(m＋1) C、M＝mn＋1 D、M＝m(n＋1)

查看试题解析
25. 若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式，如a+b+c就是完全对称式．下列三个代数式：
①（a-b）²；②ab+bc+ca；③a²b+b²c+c²a．其中是完全对称式的是（　　）

A、①② B、①③　 C、②③ D、①②③

查看试题解析
26. 如图是用棋子摆成的图案，按照这样的规律摆下去，第⑨个图案需要的棋子个数为（）

A、 $81$ B、 $91$ C、 $109$ D、 $111$

查看试题解析
27. 观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗；③中共有11颗星，图形①中共有17颗星，……，按此规律，图形⑦的颗数是（）

A、43 B、45 C、41 D、536

查看试题解析
28. 如图，在四边形 $A B C D$ 中， $A B = A D ， B C = D C$ ，点 $P$ 为 $A C$ 上的点（不与 $A ， C$ 重合），观察下列图形中全等三角形的对数．其中，图1中有3对全等三角形，图2中有6对全等三角形，图3中有10对全等三角形，…．按此规律，第5个图中有（）对全等三角形．

A、15 B、16 C、18 D、21

查看试题解析

三、解答题

29. 观察下面一列数：-1，2，-3，4，-5，6，-7，8，-9，……

(1)、请写出这一列数中的第100个数和第2022个数．

(2)、在前2022个数中，正数和负数分别有多少个？

(3)、2023和-2023是否都在这一列数中？若在，请指出它们分别是第几个数；若不在，请说明理由．

查看试题解析
30. 探索规律，观察下面等式，解答问题．
1＝1²；
1+3＝4＝2²；
1+3+5＝9＝3²；
1+3+5+7＝16＝4²；
1+3+5+7+9＝25＝5²；
…

(1)、请猜想1+3+5+7+9+…+21＝；

(2)、请猜想1+3+5+7+9+…+（2n﹣1）＝；（n是整数且n≥1）

(3)、计算：201+203+…+297+299．

查看试题解析