【2024中考数学一轮复习】20阅读理解与新定义问题

我们定义：如果两个实数的和等于这两个实数的积，那么这两个实数就叫做“和积等数对”，即：如果$a\text{+}b=a\times b$ ， 那么a与b就叫做“和积等数对”，记为$\left(a\mathrm{，}b\right)$.

例如：$2\text{+}2=2\times 2$ ， $\frac{1}{2}+\mathrm{(}-1\mathrm{)}=\frac{1}{2}\times \mathrm{(}-1\mathrm{)}$ ， $3+\frac{3}{2}=3\times \frac{3}{2}$ ，

则称数对$\left(2\mathrm{，}2\right)$ ， $\left(\frac{1}{2}\mathrm{，}-1\right)$ ， $\left(3\mathrm{，}\frac{3}{2}\right)$是“和积等数对”.

根据上述材料，解决下列问题：

$a$＊$b$=$a^2+2ab-4$ ，

例如：1＊2=1²+2×1×2$-$4=1.求：

一般地，n个相同的因数a相乘$\underset{\text{n}\text{个}}{\underbrace{\text{a}\mathrm{•}\text{a}\dots \text{a}}}$记为aⁿ ． 如2×2×2=2³=8，此时，3叫做以2为底8的对数，记为log₂8（即log₂8=3）．一般地，若aⁿ=b（a＞0且a≠1，b＞0），则n叫做以a为底b的对数，记为log_ab（即log_ab=n）．如3⁴=81，则4叫做以3为底81的对数，记为log₃81（即log₃81=4）．

例如：分解因式：$x^2+2x\text{﹣}3$ ．

解：原式$=\left(x^2+2x+l\right)\text{﹣}4={\left(x+1\right)}^2\text{﹣}4=\left(x+1+2\right)\mathrm{(}x+1\text{﹣}2\mathrm{)}=\left(x+3\right)\mathrm{(}x\text{﹣}1\mathrm{)}$ 

再如：求代数式$2x^2+4x\text{﹣}6$ 的最小值．

解：$2x^2+4x\text{﹣}6=2\mathrm{(}{x}^2+2x\text{﹣}3\mathrm{)}=2{\left(x+1\right)}^2\text{﹣}8$ ，可知当$x=\text{﹣}1$ 时，$2x^2+4x\text{﹣}6$有最小值，最小值是－8．

根据阅读材料，用配方法解决下列问题：

结合上述素材，完成以下问题：

【模型理解】

问题提出：某兴趣小组开展综合实践活动：在$\text{R}\text{t}\text{△}ABC$中，$\angle C=90°$ ， D为$AC$上一点，$CD=\sqrt{2}$ ， 动点P以每秒1个单位的速度从C点出发，在三角形边上沿$C\to B\to A$匀速运动，到达点A时停止，以$DP$为边作正方形$DPEF$设点P的运动时间为$t\text{s}$ ， 正方形$DPEF$的面积为S ， 探究S与t的关系.

1▽3=1×3+3=6， 3▽1=3×1+1=4， 5▽4=5×4+4=24，请你想一想：

[材料阅读]平面内两点M(x₁ ， y₁)，N(x₂ ， y₂)，则由勾股定理可得，这两点间的距离MN=$\sqrt{\mathrm{(}{x}_1-x_2{\mathrm{)}}^2+\mathrm{(}{y}_1-y_2{\mathrm{)}}^2}$ ．

例如，如图1，M(3，1)，N(，-2)，则MN=$\sqrt{\mathrm{(}3-1{\mathrm{)}}^2+\mathrm{(}1+2{\mathrm{)}}^2}=\sqrt{13}$ ．

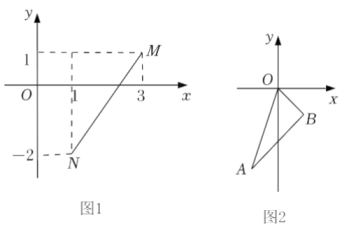
[直接应用]

定义：如果一个数的平方等于-1，记为$i_{}^2$=-1，这个数i叫做虚数单位。那么和我们所学的实数对应起来就叫做复数，表示为$a+bi$（a，b为实数），a叫这个复数的实部，b叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似。

例如计算：$\mathrm{(}5+i\mathrm{)}\times \mathrm{(}3-4i\mathrm{)}=19-17i$.

符号$\left|\begin{array}{cc}\mathrm{a}& \mathrm{c}\\ \mathrm{b}& \mathrm{d}\end{array}\right|，$称为二阶行列式，规定它的运算法则为$\left|\begin{array}{cc}\mathrm{a}& \mathrm{c}\\ \mathrm{b}& \mathrm{d}\end{array}\right|=\mathrm{a}\mathrm{d}-\mathrm{b}\mathrm{c}.$例如$\left|\begin{array}{cc}3& 5\\ 2& 4\end{array}\right|=3$×4-2×5=2.

请根据以上材料，化简下面的二阶行列式：

$\left|\begin{array}{cc}\frac{\mathrm{a}}{\mathrm{a}-1}& \mathrm{a}+1\\ \frac{1}{1-\mathrm{a}}& 1\end{array}\right|.$

例如：$4x-2x+x=\left(4-2+1\right)x=3x$ ， 类似地，我们把$\left(a-b\right)$看成一个整体，则$4\left(a-b\right)-2\left(a-b\right)+\left(a-b\right)=\left(4-2+1\right)\left(a-b\right)=3\left(a-b\right)$ ．

【尝试应用】根据阅读内容，运用“整体思想”，解答下列问题：

解；设32-x=a．x-12= b，则（32-x）（x-12）= ab= 100，a+b= （32-x） +（x-12） = 20，（32-x）²+（x-12）²=a²+b²= （a+b）²- 2ab = 20²-2×100=200．

我们把这种方法叫做换元法，利用换元法达到简化方程的目的，体现了转化的数学思想．

[解决问题]

如$2÷2÷2$ ， $\mathrm{(}-3\mathrm{)}÷\mathrm{(}-3\mathrm{)}÷\mathrm{(}-3\mathrm{)}÷\mathrm{(}-3\mathrm{)}$等．类比有理数的乘方，我们把2÷2÷2记作，读作“2的圈3次方”；$\mathrm{(}-3\mathrm{)}÷\mathrm{(}-3\mathrm{)}÷\mathrm{(}-3\mathrm{)}÷\mathrm{(}-3\mathrm{)}$记作，读作“-3的圈4次方”．对于a^ⓝ（a≠0），读作“a的圈 n次方”．

我们规定一种新的运算法则：$\left[\begin{array}{ll}a\hfill & c\hfill \\ b\hfill & d\hfill \end{array}\right]=a+b-c-d$ ， $\left(\begin{array}{ll}a\hfill & c\hfill \\ b\hfill & d\hfill \end{array}\right)=a-b+c-d$ ， 其中每个运算法则的右边都是我们学过的有理数的加减法.

请阅读下列材料，并完成相应的任务：

阿尔·花拉子米(约780~约850)，著名阿拉伯数学家、天文学家、地理学家，是代数与算术的整理者，被誉为“代数之父”．他利用正方形图形巧妙解出了一元二次方程$x^2+2x-35=0$的一个解．将边长为x的正方形和边长为1的正方形，外加两个长方形，长为x，宽为1，拼合在一起面积就是$x^2+2x\times 1+1^2$ ，即$x^2+2x+1$ ， 而由原方程$x^2+2x-35=0$变形得$x^2+2x+1=35+1$ ， 即边长为x+1的正方形面积为36．所以${\left(x+1\right)}^2=36$ ， 则x=5．

任务：

阿尔·花拉子米（约780 $\sim$ 约850），著名阿拉伯数学家、天文学家、地理学家，是代数与算术的整理者，被誉为“代数之父”．他利用正方形图形巧妙解出了一元二次方程 $x^2+2x-35=0$ 的一个解．

将边长为x的正方形和边长为1的正方形，外加两个长方形，长为x ， 宽为1，拼合在一起面积就是 $x^2+2\cdot x\cdot 1+1^2$ ，即 $x^2+2x+1$ ，而由原方程 $x^2+2x-35=0$ 变形得 $x^2+2x+1=35+1$ ，即边长为 $x+1$ 的正方形面积为36．所以 ${(x+1)}^2=36$ ，则 $x=5$ ．

将以上三个等式两边分别相加得：

$\frac{1}{1\times 2}\text{+}\frac{1}{2\times 3}\text{+}\frac{1}{3\times 4}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}=1-\frac{1}{4}=\frac{3}{4}$ ．

[推理能力、运算能力]在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论思想解决问题的过程，请仔细阅读，并解答问题．

[提出问题]三个有理数$a\mathrm{，}b\mathrm{，}c$满足$abc>0$ ， 求$\frac{\left|a\right|}{a}+\frac{\left|b\right|}{b}+\frac{\left|c\right|}{c}$的值．

[解决问题]由题意可知$a\mathrm{，}b\mathrm{，}c$三个有理数都为正数或其中一个为正数，另外两个为负数．

①当$a\mathrm{，}b\mathrm{，}c$都为正数，即$a>0\mathrm{，}b>0\mathrm{，}c>0$时，$\frac{\left|a\right|}{a}+\frac{\left|b\right|}{b}+\frac{\left|c\right|}{c}=\frac{a}{a}+\frac{b}{b}+\frac{c}{c}=1+1+1=3$；

②当$a\mathrm{，}b\mathrm{，}c$中有一个为正数，另外两个为负数时，不妨设$a>0\mathrm{，}b<0\mathrm{，}c<0$ ， 则$\frac{\left|a\right|}{a}+\frac{\left|b\right|}{b}+\frac{\left|c\right|}{c}=\frac{a}{a}+\frac{-b}{b}+\frac{-c}{c}=1+\left(-1\right)+\left(-1\right)=-1$ ．

综上所述，$\frac{\left|a\right|}{a}+\frac{\left|b\right|}{b}+\frac{\left|c\right|}{c}$的值为3或$-1$ ．

[探究拓展]请根据上面的解题思路解答下面的问题：

证明如下：过E点作EF∥AB．

  $\therefore$ ∠B=∠1(两直线平行，内错角相等．）

又 $\because$ AB∥CD(已知）

  $\therefore$ CD∥EF(如果两条直线都与第三条直线平行，那么这两条直线也互相平行．） 

  $\therefore$ ∠2=∠D(两直线平行，内错角相等．）

  $\therefore$ ∠1+∠2=∠B+∠D(等式的性质1．）

 即：∠E=∠B+∠D

配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值、最小值等问题．

例如：分解因式：$x^2+2x-3$

解：原式$=\left(x^2+2x+1\right)-1-3={\left(x+1\right)}^2-4=\left(x+1+2\right)\left(x+1-2\right)=\left(x+3\right)\left(x-1\right)$

再如：求代数式$x^2+2x-3$的最小值．

解：原式$=\left(x^2+2x+1\right)-1-3={\left(x+1\right)}^2-4$

又$\text{∵}{\left(x+1\right)}^2$是一个非负数，

$\therefore {\left(x+1\right)}^2\ge 0$ ．

$\therefore {\left(x+1\right)}^2-4\ge -4$ ．

可知当$x=-1$时，$x^2+2x-3$有最小值，最小值是$-4$ ．

根据阅读材料，用配方法解决下列问题：