人教版初中数学九年级下学期 第二十七章 相似 单元测试 B卷
试卷更新日期:2024-03-15 类型:单元试卷
一、选择题
-
1. 若= , 则的值为( )A、 B、 C、1 D、2. 如图,和△是以点为位似中心的位似三角形,若为的中点, , 则的面积为
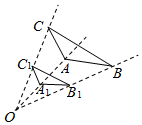 A、15 B、12 C、9 D、63. 如图,将△ABC的AB边与刻度尺的边缘重合,点A,D,B分别对应刻度尺上的整数刻度.已知 , , , 下列结论不正确的是( )
A、15 B、12 C、9 D、63. 如图,将△ABC的AB边与刻度尺的边缘重合,点A,D,B分别对应刻度尺上的整数刻度.已知 , , , 下列结论不正确的是( ) A、 B、 C、 D、4. 如图,安装路灯AB的路面CD比种植树木的地面PQ高CP=1.2 m,在路灯的照射下,路基CP留在地面上的影长EP为0.4 m,通过测量知道BC的距离为1.5 m,则路灯AB的高度是( )
A、 B、 C、 D、4. 如图,安装路灯AB的路面CD比种植树木的地面PQ高CP=1.2 m,在路灯的照射下,路基CP留在地面上的影长EP为0.4 m,通过测量知道BC的距离为1.5 m,则路灯AB的高度是( ) A、3 m B、3.6 m C、4.5 m D、6 m5. 如图, 已知 , 则 CE的长为 ( )
A、3 m B、3.6 m C、4.5 m D、6 m5. 如图, 已知 , 则 CE的长为 ( ) A、 B、 C、6 D、6. 下列说法中正确的是( )A、两个面积相等的三角形是全等三角形 B、三个对应角都相等的三角形是全等三角形 C、两个周长相等的三角形是全等三角形 D、两个完全重合的三角形是全等三角形7. 如图,在正方形ABCD中,AB=4,AC与 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交 于点N′,则PN-MN′的值为( )
A、 B、 C、6 D、6. 下列说法中正确的是( )A、两个面积相等的三角形是全等三角形 B、三个对应角都相等的三角形是全等三角形 C、两个周长相等的三角形是全等三角形 D、两个完全重合的三角形是全等三角形7. 如图,在正方形ABCD中,AB=4,AC与 相交于点O,N是AO的中点,点M在BC边上,P是OD的中点,过点P作PM⊥BC于点M,交 于点N′,则PN-MN′的值为( )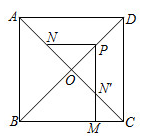 A、 B、 C、 D、8. 如图,正方形的边长为12,E是中点,F是对角线上一点,且 , 在上取点G,使得 , 交于H,则的长为( )
A、 B、 C、 D、8. 如图,正方形的边长为12,E是中点,F是对角线上一点,且 , 在上取点G,使得 , 交于H,则的长为( ) A、4 B、 C、 D、9. 如图,在正方形ABCD中,M是边CD上一点,满足 , 连接BM交AC于点N,延长BN到点P使得 , 则( )
A、4 B、 C、 D、9. 如图,在正方形ABCD中,M是边CD上一点,满足 , 连接BM交AC于点N,延长BN到点P使得 , 则( ) A、 B、 C、 D、10. 如图,是等边三角形,D , E分别是 , 边上的点,且 , 连接 , 相交于点F , 则下列说法正确的是( )
A、 B、 C、 D、10. 如图,是等边三角形,D , E分别是 , 边上的点,且 , 连接 , 相交于点F , 则下列说法正确的是( )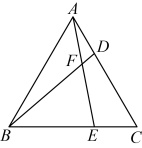
①; ②;③;④若 , 则
A、①②③ B、①②④ C、②③④ D、①③④二、填空题
-
11. 若均不为0),那么.12. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.
 13. 如图,△ABC与△DEF是位似图形,点O是位似中心,OB:BE=1,若S△ABC=2,则S△DOF= .
13. 如图,△ABC与△DEF是位似图形,点O是位似中心,OB:BE=1,若S△ABC=2,则S△DOF= .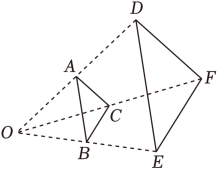 14. 如图,点在反比例函数的图象上,点在轴负半轴上,交轴于点 , 若:: , , 则的值为 .
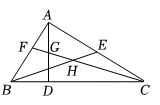
14. 如图,点在反比例函数的图象上,点在轴负半轴上,交轴于点 , 若:: , , 则的值为 . 15. 如图,在中, , , 是边上的高,是边的中线,是的角平分线,交于点 , 交于点.
15. 如图,在中, , , 是边上的高,是边的中线,是的角平分线,交于点 , 交于点.①;②;③;④.
其中一定正确的是.(写出所有正确结论的序号)
三、解答题
-
16. 已知:如图,四边形ABCD中,为对角线BD的中点,点在边AD上,CF交BD于点.
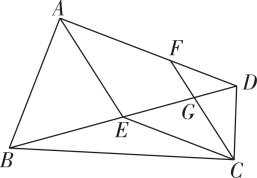 (1)、求证:四边形AECF为菱形;(2)、 , 求证:.17. 如图,点分别在三边上,且 , .
(1)、求证:四边形AECF为菱形;(2)、 , 求证:.17. 如图,点分别在三边上,且 , . (1)、求的长;(2)、若的面积为4,求四边形的面积.18. 如图,在平行四边形中,为边上一点, .
(1)、求的长;(2)、若的面积为4,求四边形的面积.18. 如图,在平行四边形中,为边上一点, . (1)、求证:∽;
(1)、求证:∽;
(2)、若 , , 求的长.四、实践探究题
-
19. 如图

【问题原型】华师版教材八年级下册第121页有这样一道题:
如图1,在正方形ABCD中,CE⊥DF.求证:CE=DF.
请你完成这一问题的证明过程.
【问题应用】如图,在正方形ABCD中,AB=4,E、F分别是边AB、BC上的点,且AE=BF.
(1)、如图2,连接CE、DF交于点G,H为GE的中点,连接DH,FH.当E为AB的中点时,四边形CDHF的面积为 ;(2)、如图3,连接DE、DF,当点E在边AB上运动时,DE+DF的最小值为 .20. 【阅读】如图1,若△ABD∽△ACE , 且点B , D , C在同一直线上,则我们把△ABD与△ACE称为旋转相似三角形.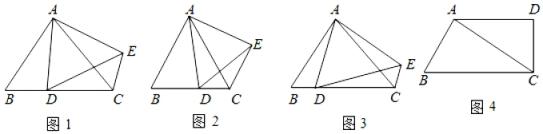 (1)、【理解】如图2,△ABC和△ADE是等边三角形,点D在边BC上,连接CE . 求证:△ABD与△ACE是旋转相似三角形.(2)、【应用】如图3,△ABD与△ACE是旋转相似三角形,AD∥CE , 求证:AC=DE .(3)、【拓展】如图4,AC是四边形ABCD的对角线,∠D=90°,∠B=∠ACD , BC=25,AC=20,AD=16,试在边BC上确定一点E , 使得四边形AECD是矩形,并说明理由.21. 某校项目式学习小组开展项目活动,过程如下:
(1)、【理解】如图2,△ABC和△ADE是等边三角形,点D在边BC上,连接CE . 求证:△ABD与△ACE是旋转相似三角形.(2)、【应用】如图3,△ABD与△ACE是旋转相似三角形,AD∥CE , 求证:AC=DE .(3)、【拓展】如图4,AC是四边形ABCD的对角线,∠D=90°,∠B=∠ACD , BC=25,AC=20,AD=16,试在边BC上确定一点E , 使得四边形AECD是矩形,并说明理由.21. 某校项目式学习小组开展项目活动,过程如下:项目主题:测量旗杆高度

问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,比如自制的直角三角形硬纸板,标杆,镜子,甚至还可以利用无人机…确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的部分测量方案:
方案一
方案二
…
测量工具
标杆,皮尺
自制直角三角板硬纸板,皮尺
…
测量示意图

说明:线段AB表示学校旗杆,小明的眼睛到地面的距离CD=1.7m,测点F与B,D在同一水平直线上,D,F,B之间的距离都可以直接测得,且A,B,C,D,E,F都在同一竖直平面内,点A,C,E三点在同一直线上.

说明:线段AB表示旗杆,小明的身高CD=1.7m,测点D与B在同一水平直线上,D,B之间的距离可以直接测得,且A,B,C,D,E,F,G都在同一竖直平面内,点A,C,E三点在同一直线上,点C,F,G三点在同一直线上.
测量数据
B,D之间的距离
16.8m
B,D之间的距离
16.8m
…
D,F之间的距离
1.35m
EF的长度
0.50m
…
EF的长度
2.60m
CE的长度
0.75m
…
…
…
根据上述方案及数据,请你选择一个方案,求出学校旗杆AB的高度.(结果精确到0.1m);
五、综合题

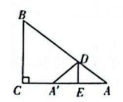 图2
图2  图3
图3