人教版初中数学九年级下学期 第二十七章 相似 单元测试 A卷
试卷更新日期:2024-03-15 类型:单元试卷
一、选择题
-
1. 如果 , 那么( )A、 B、 C、 D、2. 以下列长度(同一单位)为长的四条线段中,成比例的是( )A、1,2,3,4 B、2,4,8,16 C、2,12,12,4 D、2,10,15,53. 如图,已知 , , 若的长度为6,则的长度为( )
 A、4 B、9 C、12 D、4. 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=2,BC=4,EF=3,则DE的长为 ( )
A、4 B、9 C、12 D、4. 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=2,BC=4,EF=3,则DE的长为 ( )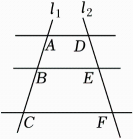 A、1 B、1.5 C、2 D、2.55. 下列各组图形中,一定相似的是( )A、两个平行四边形 B、两个正方形 C、两个菱形 D、两个矩形6. 如图,把△AOB缩小后得到△COD , 则△COD与△AOB的相似比为( )
A、1 B、1.5 C、2 D、2.55. 下列各组图形中,一定相似的是( )A、两个平行四边形 B、两个正方形 C、两个菱形 D、两个矩形6. 如图,把△AOB缩小后得到△COD , 则△COD与△AOB的相似比为( ) A、 B、 C、 D、7. 如图,是某商店售卖的花架简图,其中 , , , , 则长为( ) .
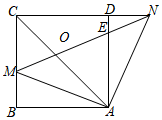
A、 B、 C、 D、7. 如图,是某商店售卖的花架简图,其中 , , , , 则长为( ) . A、 B、 C、50 D、308. 如图,在中,点D在BC边上,连接AD , 点C在线段AD上, , 且交AD于点E , , 且交CD于点F , 则下列结论一定正确的是( )
A、 B、 C、50 D、308. 如图,在中,点D在BC边上,连接AD , 点C在线段AD上, , 且交AD于点E , , 且交CD于点F , 则下列结论一定正确的是( ) A、 B、 C、 D、9. 如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC= , 则△ABC移动的距离是( )
A、 B、 C、 D、9. 如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC= , 则△ABC移动的距离是( ) A、 B、 C、 D、﹣10. 如图,在中,平分 , 按如下步骤作图:
A、 B、 C、 D、﹣10. 如图,在中,平分 , 按如下步骤作图: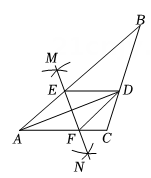
第一步,分别以点、为圆心,以大于的长为半径在两侧作弧,交于两点、;
第二步,连接分别交、于点、;
第三步,连接、 .
若 , , , 则的长是
A、3 B、4 C、5 D、6二、填空题
-
11. 已知 ,若b+d≠0,则 = .12. 如图,乐器上的一根弦的长度为 , 两个端点、固定在乐器板面上,支撑点是弦靠近点的黄金分割点,则线段的长度为.(结果保留根号,参考数据:黄金分割数:).
 13. 如图,原点是和的位似中心,点与点是对应点,的面积是3,则的面积是 .
13. 如图,原点是和的位似中心,点与点是对应点,的面积是3,则的面积是 . 14. 如图, 4 个小正方形拼成 “ ” 型模具, 其中三个顶点在正坐标轴上, 顶点 在反比例函数 的图象上, 若 , 则 .
14. 如图, 4 个小正方形拼成 “ ” 型模具, 其中三个顶点在正坐标轴上, 顶点 在反比例函数 的图象上, 若 , 则 .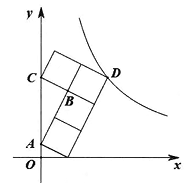 15. 如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .
15. 如图,在 中, , , , ,垂足为 , 为 的中点, 与 交于点 ,则 的长为 .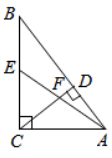
三、解答题
-
16. 如图,在中,点D、E分别在边AC、AB上,.
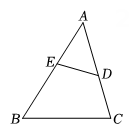
求证:.
17. 如图,在△ABC中,BM平分∠ABC , MB=MC . (1)、求证:△AMB∽△ABC;(2)、若AM=3,MB=6,求AB的长.18. 如图1,滹沱河是山西地区一条途经了舟山和太行山的知名河流,这条河流的流域面积达到了2.73万平方公里,其发源地处于山西省繁峙县泰戏山桥儿沟村,这条河流早在《山海经》中就有出现过,被叫做为虔池.为了估算河流的宽度,我们在河的对岸选定一个目标P , 在近岸取点A和C , 使点P、A、C共线且与河垂直,接着在过点C且与直线PC垂直的直线上选择适当的点D , 确定PD与过点A且与PC垂直的直线交点B , 测得AC=50m , CD=120m , AB=80m , 请根据这些数据求河的宽度PA .
(1)、求证:△AMB∽△ABC;(2)、若AM=3,MB=6,求AB的长.18. 如图1,滹沱河是山西地区一条途经了舟山和太行山的知名河流,这条河流的流域面积达到了2.73万平方公里,其发源地处于山西省繁峙县泰戏山桥儿沟村,这条河流早在《山海经》中就有出现过,被叫做为虔池.为了估算河流的宽度,我们在河的对岸选定一个目标P , 在近岸取点A和C , 使点P、A、C共线且与河垂直,接着在过点C且与直线PC垂直的直线上选择适当的点D , 确定PD与过点A且与PC垂直的直线交点B , 测得AC=50m , CD=120m , AB=80m , 请根据这些数据求河的宽度PA .
四、实践探究题
-
19. 【教材呈现】华师版九年级上册63页例1.
如图,在△ABC中,点D是边AB的三等分点,DE∥BC,DE=5,求BC的长.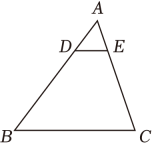
【应用拓展】
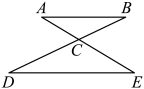
(1)、如图①,在△ABC中,点D是边AB的中点,点F为BC延长线上一点,连接DF交AC于点E,若DE:EF=3:1,DG∥AC,EC=2,则AC的长为 . (2)、如图②,在△ABC中,点D为边BA延长线上一点,点E为BC上一点,连接DE交AC于点F,若点A为DB的中点,CE:EB=1:2,△DBE的面积为4,则△CFE(阴影部分)面积为 .
(2)、如图②,在△ABC中,点D为边BA延长线上一点,点E为BC上一点,连接DE交AC于点F,若点A为DB的中点,CE:EB=1:2,△DBE的面积为4,则△CFE(阴影部分)面积为 . 20. 根据以下素材,探索解决问题.
20. 根据以下素材,探索解决问题.测量旗杆的高度

素材1 可以利用影子测量旗杆的高度.如图1,光线 , DN,BM分别是旗杆和小陈同学在同一时刻的影子.
素材2 可以利用镜子测量旗杆的高度.如图2,小陈同学从镜子E中刚好可以看见旗杆的顶端C,测得.
素材3 可以利用标杆测量旗杆的高度.如图3,点G,P,C在同一直线上,标杆 , 测得 , . (说明:小陈同学、旗杆CD与标杆PQ均垂直于地面,小陈同学的眼睛G离地面的距离)
(1)、任务1 利用素材1证明△ABM△CDN;(2)、任务2 在素材2中,小陈同学还要测量图中哪条线段的长度(旗杆无法直接测量),才能求出旗杆的高度?若把该线段的长度记为a,请你用含a的式子表示出旗杆的高度;(3)、任务3 利用素材3求出旗杆的高度.五、综合题
-
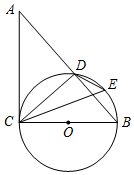
21. 已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GE•GD.
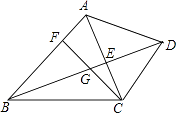 (1)、求证:∠ACF=∠ABD;(2)、连接EF,求证:EF•CG=EG•CB.
(1)、求证:∠ACF=∠ABD;(2)、连接EF,求证:EF•CG=EG•CB.