人教版初中数学九年级下学期 第二十六章 反比例函数 单元测试 B卷
试卷更新日期:2024-03-15 类型:单元试卷
一、选择题
-
1. 下列说法正确的是A、对角线垂直的平行四边形是矩形 B、方程有两个相等的实数根 C、抛物线的顶点为 D、函数 , 随的增大而增大2. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、3. 某综合实践活动小组设计了简易电子体重秤: 制作一个装有踏板(踏板质量忽略不计)的可变电阻 (如图 1), 当人站上踏板时, 通过电压表显示的读数 换算为人的质量 ), 已知 随着 的变化而变化 (如图 2), 与踏板上人的质量 的关系见图3. 则下列说法不正确的是 ( )
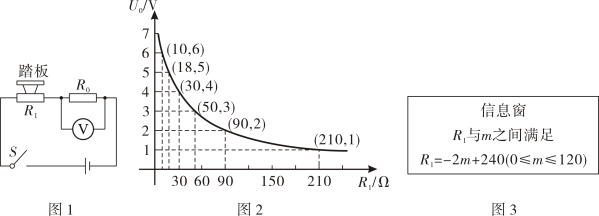 A、在一定范围内, 越大, 越小 B、当 时, 的阻值为 C、当踏板上人的质量为 时, D、若电压表量程为 , 为保护电压表, 该电子体重科可称的最大质量是4. 如图,一次函数的图象与反比例函数的图象交于点 , 则不等式的解是( )
A、在一定范围内, 越大, 越小 B、当 时, 的阻值为 C、当踏板上人的质量为 时, D、若电压表量程为 , 为保护电压表, 该电子体重科可称的最大质量是4. 如图,一次函数的图象与反比例函数的图象交于点 , 则不等式的解是( ) A、或 B、或 C、或 D、或5. 若点在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、6. 反比例函数的图象如图所示,轴,若的面积为 , 则的值为( )
A、或 B、或 C、或 D、或5. 若点在反比例函数的图象上,则的大小关系是( )A、 B、 C、 D、6. 反比例函数的图象如图所示,轴,若的面积为 , 则的值为( ) A、 B、 C、 D、7. 在同一直角坐标系中,函数与的图象可能是( )A、
A、 B、 C、 D、7. 在同一直角坐标系中,函数与的图象可能是( )A、 B、
B、 C、
C、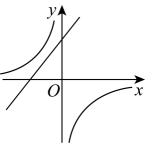 D、
D、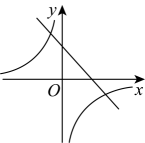 8.
8.如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, . ∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=的图象过点C.当以CD为边的正方形的面积为时,k的值是( )
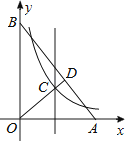 A、2 B、3 C、5 D、79. 已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t , p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠-2),点C(t , m)和点D(t+2,n)在函数的图象上.当p-m与q-n的积为负数时,t的取值范围是( )A、或 B、或 C、-3<t<-2或-1<t<0 D、-3<t<-2或0<t<110. 如图,直线与双曲线交于两点,轴于点 , 连接交轴于点。下列结论:①;②的面积为定值;③是的中点;④ . 其中正确的结论有( )
A、2 B、3 C、5 D、79. 已知在平面直角坐标系中,正比例函数y=k1x(k1>0)的图象与反比例函数(k2>0)的图象的两个交点中,有一个交点的横坐标为1,点A(t , p)和点B(t+2,q)在函数y=k1x的图象上(t≠0且t≠-2),点C(t , m)和点D(t+2,n)在函数的图象上.当p-m与q-n的积为负数时,t的取值范围是( )A、或 B、或 C、-3<t<-2或-1<t<0 D、-3<t<-2或0<t<110. 如图,直线与双曲线交于两点,轴于点 , 连接交轴于点。下列结论:①;②的面积为定值;③是的中点;④ . 其中正确的结论有( )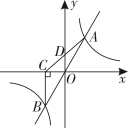 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若点和点都在反比例函数的图象上,则 . (用“”“”或“”填空)12. 近视眼镜的度数y度与镜片焦距x米呈反比例,其函数关系式为 如果近似眼镜镜片的焦距 米,那么近视眼镜的度数y为 .
13. 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y= (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .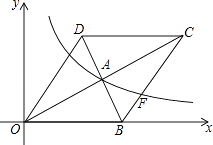 14. 如图,在平面直角坐标系中,□CODE的顶点C 在x轴的负半轴上,点D,E在第二象限,点E的纵坐标为2,反比例函数 的图象与OD 相交于点A(a,b).若点 B的坐标为 且点B 在∠ODE的边上,则 OB 的长.为.
14. 如图,在平面直角坐标系中,□CODE的顶点C 在x轴的负半轴上,点D,E在第二象限,点E的纵坐标为2,反比例函数 的图象与OD 相交于点A(a,b).若点 B的坐标为 且点B 在∠ODE的边上,则 OB 的长.为.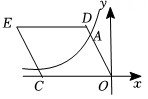 15. 如图, ▱ OABC的顶点O 是坐标原点,点 A 在x 轴的正半轴上,点 B,C在第一象限,反比例函数 , y=kx(k≠0)的图象分别经过点 C,B.若 OC=AC,则k的值为.
15. 如图, ▱ OABC的顶点O 是坐标原点,点 A 在x 轴的正半轴上,点 B,C在第一象限,反比例函数 , y=kx(k≠0)的图象分别经过点 C,B.若 OC=AC,则k的值为.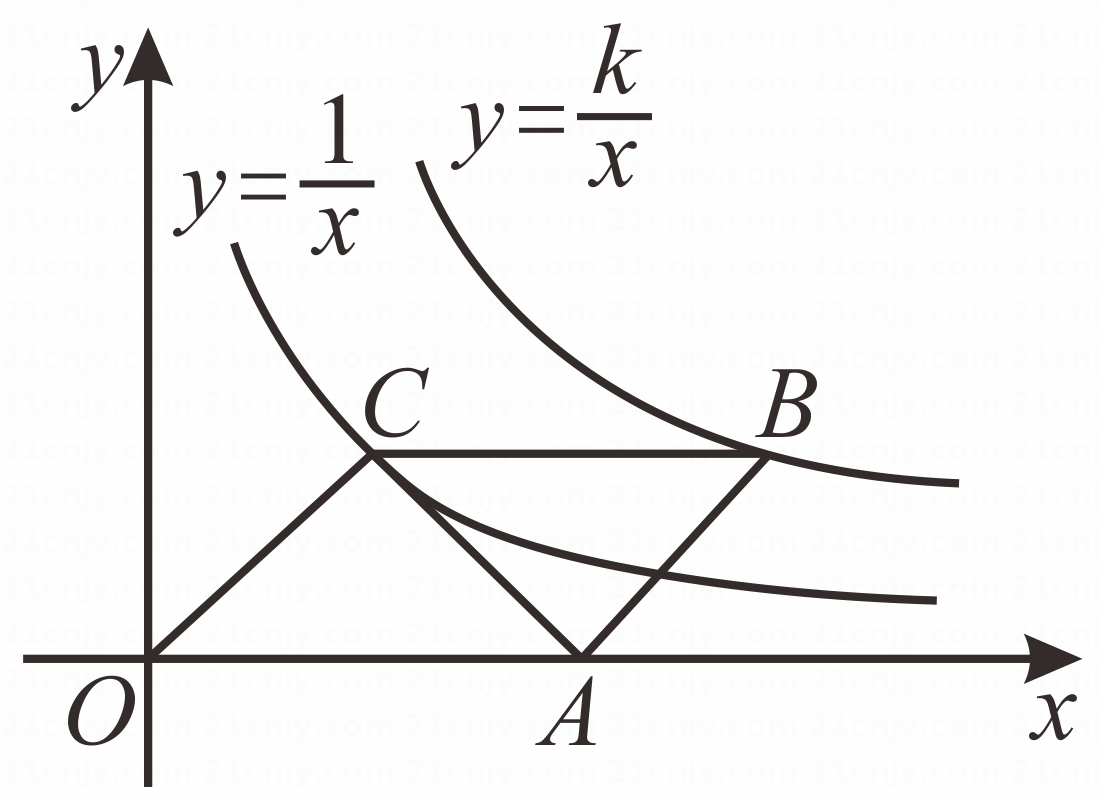
三、解答题
-
16. 已知反比例函数的图象位于第二、四象限.(1)、求k的取值范围;(2)、若点是该反比例函数图象上的两点,试比较函数值的大小.17. 已知反比例函数(为常数).(1)、若函数图象经过点 , 求的值;(2)、若时,随的增大而减小,求的取值范围.18. 如图,直线与双曲线(k为常数,交于 , 两点,与轴、轴分别交于 , 两点,点的坐标为 .
 (1)、求反比例函数的解析式.(2)、结合图象直接写出当时,的取值范围.
(1)、求反比例函数的解析式.(2)、结合图象直接写出当时,的取值范围.四、实践探究题
-
19. 背景:点A在反比例函数y=(k>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形.如图1,点A在第一象限内,当AC=4时,小李测得CD=3.
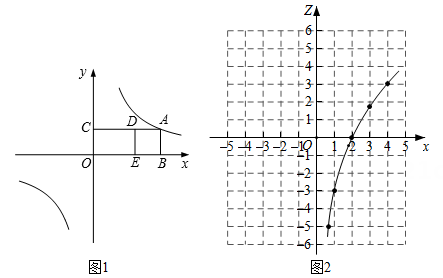
探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在函数关系.请帮助小李解决下列问题.
(1)、求k的值.(2)、设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”.如图2,小李画出了x>0时“Z函数”的图象.①求这个“Z函数”的表达式.
②补画x<0时“Z函数”的图象,并写出这个函数的性质(两条即可).
③过点(3,2)作一直线,与这个“Z函数”图象仅有一个交点,求该交点的横坐标.
20.【综合实践】
如图所示,是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境(杠杆原理:阻力×阻力臂=动力×动力臂,如图,即FA×L1=FB×L2),受桔槔的启发,小杰组装了如图所示的装置.其中,杠杆可绕支点O在竖直平面内转动,支点O距左端L1=1m , 距右端L2=0.4m , 在杠杆左端悬挂重力为80N的物体A .
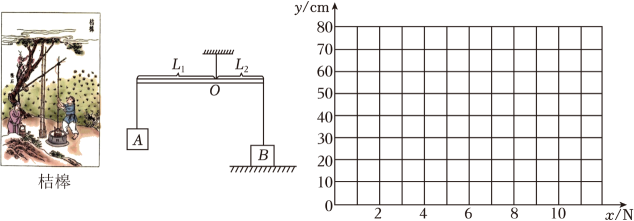 (1)、若在杠杆右端挂重物B , 杠杆在水平位置平衡时,重物B所受拉力为N .(2)、为了让装置有更多的使用空间,小杰准备调整装置,当重物B的质量变化时,L2的长度随之变化.设重物B的质量为xN , L2的长度为ycm . 则:
(1)、若在杠杆右端挂重物B , 杠杆在水平位置平衡时,重物B所受拉力为N .(2)、为了让装置有更多的使用空间,小杰准备调整装置,当重物B的质量变化时,L2的长度随之变化.设重物B的质量为xN , L2的长度为ycm . 则:①y关于x的函数解析式是 ▲ .
②完成下表:
x/N
…
10
20
30
40
50
…
y/cm
…
8
a
2
b
…
③在直角坐标系中画出该函数的图象.
(3)、在(2)的条件下,将函数图象向右平移4个单位长度,与原来的图象组成一个新的函数图象,记为L . 若点A的坐标为(2,0),在L上存在点Q , 使得S△OAQ=9.请直接写出所有满足条件的点Q的坐标.五、综合题
-
21. 已知:如图,在平面直角坐标系中,一次函数 与反比例函数 的图象交于点 和点 ,与 轴交于点 ,
 (1)、求 的值及点 的坐标;(2)、写出 时 的取值范围;(3)、 是 轴上一点,且满足 的面积等于 .求点 坐标.22. 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数(k<0)的图象交于第二、四象限内的A , B两点,与x轴交于C点,过点A作AD⊥y轴,垂足为点D , OD=3, , 点B的坐标为(c , ﹣2).
(1)、求 的值及点 的坐标;(2)、写出 时 的取值范围;(3)、 是 轴上一点,且满足 的面积等于 .求点 坐标.22. 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数(k<0)的图象交于第二、四象限内的A , B两点,与x轴交于C点,过点A作AD⊥y轴,垂足为点D , OD=3, , 点B的坐标为(c , ﹣2). (1)、求该反比例函数和一次函数的表达式;(2)、根据图象直接写出使ax+b<成立的x的取值范围;(3)、形如x2﹣a>0(a为常数,a>0)的解集为:x>或x<﹣ , 过点M(6,0)作垂直于x轴的直线MN , 直线y=x+n与双曲线y=(k<0)交于点P(x1 , y1),Q(x2 , y2),与直线MN交于点R(x3 , y3),若y1<y2<y3时,求n的取值范围.23. 如图,抛物线与双曲线相交于点A、B.已知点B的坐标为 , 点A在第一象限内,且点A的横坐标为1.过点A作直线轴,交抛物线于另一点C.
(1)、求该反比例函数和一次函数的表达式;(2)、根据图象直接写出使ax+b<成立的x的取值范围;(3)、形如x2﹣a>0(a为常数,a>0)的解集为:x>或x<﹣ , 过点M(6,0)作垂直于x轴的直线MN , 直线y=x+n与双曲线y=(k<0)交于点P(x1 , y1),Q(x2 , y2),与直线MN交于点R(x3 , y3),若y1<y2<y3时,求n的取值范围.23. 如图,抛物线与双曲线相交于点A、B.已知点B的坐标为 , 点A在第一象限内,且点A的横坐标为1.过点A作直线轴,交抛物线于另一点C. (1)、求双曲线和抛物线的解析式;(2)、计算的面积;(3)、在抛物线上是否存在点D , 使的面积等于的面积,若存在,请你写出点D的坐标;若不存在,请你说明理由.
(1)、求双曲线和抛物线的解析式;(2)、计算的面积;(3)、在抛物线上是否存在点D , 使的面积等于的面积,若存在,请你写出点D的坐标;若不存在,请你说明理由.