人教版初中数学八年级下学期 第十七章 勾股定理 单元测试 B卷
试卷更新日期:2024-03-15 类型:单元试卷
一、选择题
-
1. 下列各组数中能作为直角三角形三边长度的是( )A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,82. 如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内,若知道图中阴影部分的面积,则一定能求出( )
 A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和3. 如图,长方形中, , , 在数轴上,若以点为圆心,的长为半径作弧交数轴于点 , 则点表示的数为
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和3. 如图,长方形中, , , 在数轴上,若以点为圆心,的长为半径作弧交数轴于点 , 则点表示的数为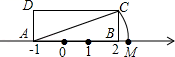 A、 B、 C、2 D、4. 如图,由六个边长为的小正方形构成一个大长方形,连接小正方形的三个顶点,可得到 , 则中边上的高是( )
A、 B、 C、2 D、4. 如图,由六个边长为的小正方形构成一个大长方形,连接小正方形的三个顶点,可得到 , 则中边上的高是( )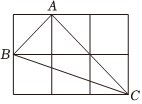 A、 B、 C、 D、5. 小华新买了一条跳绳,如图1,他按照体育老师教的方法确定适合自己的绳长:一脚踩住绳子的中央,手肘靠近身体,两肘弯屈 , 小臂水平转向两侧,两手将绳拉直,绳长即合适长度。将图1抽象成如图2,若两手握住的绳柄两端距离约为1米,小臂到地面的距离约1. 2米,则适合小华的绳长为( )
A、 B、 C、 D、5. 小华新买了一条跳绳,如图1,他按照体育老师教的方法确定适合自己的绳长:一脚踩住绳子的中央,手肘靠近身体,两肘弯屈 , 小臂水平转向两侧,两手将绳拉直,绳长即合适长度。将图1抽象成如图2,若两手握住的绳柄两端距离约为1米,小臂到地面的距离约1. 2米,则适合小华的绳长为( ) A、2. 2米 B、2. 4米 C、2. 6米 D、2. 8米6. 如图,一个长方体形盒子的长、宽、高分别为厘米、厘米、厘米,在长方体一底面的顶点有一只蚂蚁,它想吃点处的食物,沿长方体侧面爬行的最短路程是( )
A、2. 2米 B、2. 4米 C、2. 6米 D、2. 8米6. 如图,一个长方体形盒子的长、宽、高分别为厘米、厘米、厘米,在长方体一底面的顶点有一只蚂蚁,它想吃点处的食物,沿长方体侧面爬行的最短路程是( ) A、厘米 B、厘米 C、厘米 D、厘米7. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为时,顶部边缘处离桌面的高度为 , 此时底部边缘处与处间的距离为 , 小组成员调整张角的大小继续探究,最后发现当张角为时(是的对应点),顶部边缘处到桌面的距离为 , 则底部边缘处与之间的距离为( )
A、厘米 B、厘米 C、厘米 D、厘米7. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动.如图,当张角为时,顶部边缘处离桌面的高度为 , 此时底部边缘处与处间的距离为 , 小组成员调整张角的大小继续探究,最后发现当张角为时(是的对应点),顶部边缘处到桌面的距离为 , 则底部边缘处与之间的距离为( ) A、 B、 C、 D、8. 如图,在中,平分交于点 , 则点到的距离是( )
A、 B、 C、 D、8. 如图,在中,平分交于点 , 则点到的距离是( )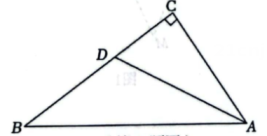 A、3 B、4 C、5 D、69. 如图,∠AOB=60°,点P是∠AOB内的定点且OP=4,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是( )
A、3 B、4 C、5 D、69. 如图,∠AOB=60°,点P是∠AOB内的定点且OP=4,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是( )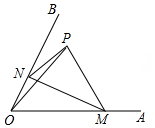 A、 B、 C、6 D、310. 如图, , D,E为BC边上的两点,且 , 连结EF,BF有下列结论:①;②△ABD等腰三角形;③∠ADC=120°;④.其中正确的个数是( )
A、 B、 C、6 D、310. 如图, , D,E为BC边上的两点,且 , 连结EF,BF有下列结论:①;②△ABD等腰三角形;③∠ADC=120°;④.其中正确的个数是( )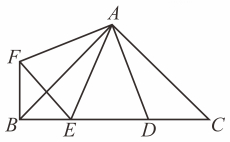 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 如图,在数轴上点 A 表示的实数是 .
 12. 如图, 中, . 以点为圆心,长为半径作弧,交于点 , 以点为圆心,长为半径作弧,交于点 . 若 , 则 .
12. 如图, 中, . 以点为圆心,长为半径作弧,交于点 , 以点为圆心,长为半径作弧,交于点 . 若 , 则 . 13. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .
13. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .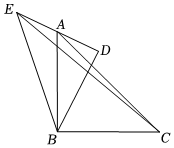 14. 如图,一架15m长的梯子AB斜靠在一竖直的墙OA上,这时梯子的顶端A离地面距离OA为12m,如果梯子顶端A沿墙下滑3m至C点,那么梯子底端B向外移至D点,则BD的长为m.
14. 如图,一架15m长的梯子AB斜靠在一竖直的墙OA上,这时梯子的顶端A离地面距离OA为12m,如果梯子顶端A沿墙下滑3m至C点,那么梯子底端B向外移至D点,则BD的长为m.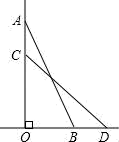 15. 如图,在平面直角坐标系xOy中,点A的坐标为(0,12),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC . 若点P为OA的中点,连接PC , 则PC的长的最小值为 .
15. 如图,在平面直角坐标系xOy中,点A的坐标为(0,12),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC . 若点P为OA的中点,连接PC , 则PC的长的最小值为 .
三、解答题
-
16. 荡秋千(图1)是中国古代北方少数民族创造的一种运动. 有一天,赵彬在公园里游玩,如图2,他发现秋千静止时,踏板离地的垂直高度 , 将它往前推送 (水平距离 )时,秋千的踏板离地的垂直高度 , 秋千的绳索始终拉得很直,求绳索的长度.
 17. 如图,△ABC中,D是BC边上的一点,若AB=10,BD=6,AD=8,AC=17.
17. 如图,△ABC中,D是BC边上的一点,若AB=10,BD=6,AD=8,AC=17. (1)、求证:AD⊥BC;(2)、求△ABC的面积,18. 如图,有一张四边形纸片 , °.经测得 , , , .
(1)、求证:AD⊥BC;(2)、求△ABC的面积,18. 如图,有一张四边形纸片 , °.经测得 , , , . (1)、求、两点之间的距离.(2)、求这张纸片的面积.
(1)、求、两点之间的距离.(2)、求这张纸片的面积.四、实践探究题
-
19. 如图
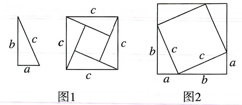 (1)、我国著名的数学家赵爽,早在公元3世纪,就把一个长方形分成四个全等的直角三角形,用四个全等的直角三角形拼成了一个大的正方形(如图1),这个图形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中两条直角边a,b与斜边满足关系式 , 称为勾股定理.
(1)、我国著名的数学家赵爽,早在公元3世纪,就把一个长方形分成四个全等的直角三角形,用四个全等的直角三角形拼成了一个大的正方形(如图1),这个图形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中两条直角边a,b与斜边满足关系式 , 称为勾股定理.证明:大正方形的面积可表示为 , 又可表示为 ,
,
.
即直角三角形两条直角边的平方和等于斜边的平方.
(2)、爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图2),也能验证这个结论,请你帮助小明完成验证的过程.20. 综合与实践:测雕塑 (1)、 如图,雕塑底座正面是四边形ABCD , 现提供一足够长的卷尺,请你设计一个方法检测雕塑底座正面的边AB是否垂直于底边BC?并说明理由.(2)、 若雕塑底座是个长方体,量得边BC长50cm,边CD长40cm,边DE长30cm,一只蚂蚁从底部点B沿雕塑的表面爬到顶部的点E , 蚂蚁爬行的最短路程是多少?
(1)、 如图,雕塑底座正面是四边形ABCD , 现提供一足够长的卷尺,请你设计一个方法检测雕塑底座正面的边AB是否垂直于底边BC?并说明理由.(2)、 若雕塑底座是个长方体,量得边BC长50cm,边CD长40cm,边DE长30cm,一只蚂蚁从底部点B沿雕塑的表面爬到顶部的点E , 蚂蚁爬行的最短路程是多少?五、综合题
-
21. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=8,BC=6,E,F分别是直线AC,AB上的动点,连结EF.
 (1)、求CD的长.(2)、若点E在边AC上,且3AE=2CE,EF⊥AC,求证:CF平分∠ACD.(3)、是否存在点E,F,使得以C,E,F为顶点的三角形与△CDF全等?若不存在,请说明理由;若存在,求出所有符合条件的DF的长.22. 若一个四边形有一组邻边相等,且这组邻边夹角所对的对角线平分一个内角,则称这样的四边形为“半对称四边形”,这条角平分线称为四边形的“分割对角线”.例如:
(1)、求CD的长.(2)、若点E在边AC上,且3AE=2CE,EF⊥AC,求证:CF平分∠ACD.(3)、是否存在点E,F,使得以C,E,F为顶点的三角形与△CDF全等?若不存在,请说明理由;若存在,求出所有符合条件的DF的长.22. 若一个四边形有一组邻边相等,且这组邻边夹角所对的对角线平分一个内角,则称这样的四边形为“半对称四边形”,这条角平分线称为四边形的“分割对角线”.例如:如图1,在四边形中, , 平分 , 则称四边形是半对称四边形,称为四边形的分割对角线.
 (1)、如图1,求证: .(2)、如图2,在四边形中, , , . 求证:四边形是半对称四边形.(3)、如图3,在中, , , , 是所在平面内一点,当四边形是半对称四边形且为分割对角线时,求四边形的面积.23. 在中, , 点为直线BC上一动点, , .
(1)、如图1,求证: .(2)、如图2,在四边形中, , , . 求证:四边形是半对称四边形.(3)、如图3,在中, , , , 是所在平面内一点,当四边形是半对称四边形且为分割对角线时,求四边形的面积.23. 在中, , 点为直线BC上一动点, , .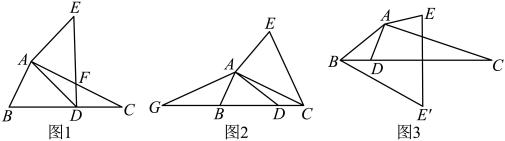 (1)、如图1,连接交于 , , 为中点,若 , , 求的长;(2)、如图2,延长至点使得 , 连接 , 求证:;(3)、如图3, , , 作点关于直线的对称点 , 连接 , , 当最小时,直接写出线段的长.
(1)、如图1,连接交于 , , 为中点,若 , , 求的长;(2)、如图2,延长至点使得 , 连接 , 求证:;(3)、如图3, , , 作点关于直线的对称点 , 连接 , , 当最小时,直接写出线段的长.