2023-2024学年初中数学人教版八年级下学期第十七章勾股定理单元测试 A卷

试卷更新日期：2024-03-15 类型：单元试卷

进入出卷网下载

一、选择题

1. 我国是最早了解勾股定理的国家之一，它被记载于我国古代著名的数学著作《周髀算经》中．下列各组数中，是“勾股数”的是（）

A、 $2 ， 3 ， 4$ B、 $4 ， 5 ， 6$ C、 $7 ， 8 ， 9$ D、 $6 ， 8 ， 10$

查看试题解析
2. 如图，两个较大的正方形的面积分别为225和289，则字母 $A$ 所代表的正方形的面积为（）

A、64 B、16 C、8 D、4

查看试题解析
3. 以下列长度的线段不能围成直角三角形的是（）

A、5，12， 13 B、 $\sqrt{2} ， \sqrt{3} ， \sqrt{5}$ C、 $\sqrt{7}$ ，3，4 D、2，3，4

查看试题解析
4. 如图，在数轴上，过表示数2的点A作数轴的垂线，以点A为圆心，1长为半径画弧，交垂线于点B，再以原点O为圆心，OB长为半径画弧，交数轴于点C，则点C表示的数为（）

A、2.1 B、2.2 C、 $\sqrt{5}$ D、 $\sqrt{7}$

查看试题解析
5. 小华用火柴棒摆直角三角形，已知他摆两条直角边分别用了6根和8根火柴棒，那么他摆完这个直角三角形共用火柴棒（）

A、10根 B、14根 C、24根 D、30根

查看试题解析
6. 如图，在 $R t △ A B C$ 中， $B C = 6$ ， $A B = 10 .$ 分别以 $B$ 、 $C$ 为圆心，以大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧分别交于 $E$ 、 $F$ 两点，连接直线 $E F$ ，分别交 $B C$ 、 $A B$ 于点 $M$ 、 $N$ ，连接 $C N$ ，则 $△ C M N$ 的面积为（）

A、 $12$ B、 $6$ C、 $7.5$ D、 $15$

查看试题解析
7. 点 $(3 ， - 1)$ 到原点的距离为（）

A、 $2 \sqrt{2}$ B、 $3$ C、 $1$ D、 $\sqrt{10}$

查看试题解析
8. 如图，一棵大树被大风刮断后，折断处离地面8m，树的顶端离树根6m，则这棵树在折断之前的高度是（）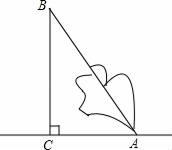

A、18m B、10m C、14m D、24m

查看试题解析
9. 已知 $△ A B C$ 的三边长分别为 $a ， b ， c$ ，且 $\sqrt{a - 6} +$ $| b - 8 | + (c - 10)^{2} = 0$ ，则 $△ A B C$ 是（）

A、以 $a$ 为斜边的直角三角形 B、以 $b$ 为斜边的直角三角形 C、以 $c$ 为斜边的直角三角形 D、等边三角形

查看试题解析
10. 如图，在 $R t △ A B O$ 中，已知 $∠ A = 90 ° ， A O = 2 ， A B = 1$ ．以 $B C = 1 ， O B$ 为直角边，构造 $R t △ O B C$ ；再以 $C D = 1 ， O C$ 为直角边，构造 $R t △ O C D$ ；…，按照这个规律，在 $R t △ O H I$ 中，点 $H$ 到 $O I$ 的距离是（）

A、 $\frac{2 \sqrt{2}}{3}$ B、 $\frac{\sqrt{33}}{6}$ C、 $\frac{3 \sqrt{10}}{10}$ D、 $\frac{\sqrt{110}}{11}$

查看试题解析

二、填空题

11. 已知Rt△ABC中，∠C=90°，a+b=14cm，c=10cm，则Rt△ABC的面积等于 cm² ．

查看试题解析
12. 如图，圆柱的底面周长是 $24 c m$ ，高是 $5 c m$ ，一只蚂蚁在 $A$ 点想吃到 $B$ 点的食物，需要爬行的最短路径是 $c m$ ．

查看试题解析
13. 如图，一个梯子斜靠在一竖直的墙 $A O$ 上，测得 $A O = 4 m$ ，若梯子的顶端沿墙下滑 $1 m$ ，这时梯子的底端也向右滑 $1 m$ ，则梯子 $A B$ 的长度为.

查看试题解析
14. 如图， $A P$ 平分 $∠ M A N$ ， $P B ⊥ A M$ 于点 $B$ ，点 $C$ 在射线 $A N$ 上，且 $A C < A B$ ．若 $P B = 3$ ， $P C = 5$ ， $A C = 2$ ，则 $A B$ 的长为．

查看试题解析
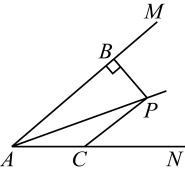15. “赵爽弦图”是我国古代数学的骄傲，它巧妙利用面积关系证明了勾股定理，如图所示的“弦图”，是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较短直角边长为a ，较长直角边长为b ，若大正方形的面积为17，每个直角三角形面积为4，那么 ${(a - b)}^{2}$ 为．

查看试题解析

三、解答题

16. 如图，在平面直角坐标系中，A(1，1)，B(3，1)，C(1，5)是三角形的三个顶点，求BC的长.

查看试题解析
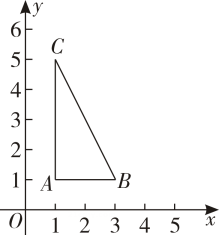17. 如图，在一次课外活动中，同学们要测量某公园人工湖两侧A，B两个凉亭之间的距离，已知CD⊥BD，现测得AC= $20 \sqrt{3} m$ ，BC= $60 m$ ，CD= $30 m$ ，请计算A，B两个凉亭之间的距离.

查看试题解析
18. 如图，扶梯 $A B$ 的坡比为 $4 ： 3$ ，滑梯 $C D$ 的坡比为 $1 ： 2 ， B C$ 平行于地面， $B E ⊥ A D$ 于点 $E ， C F ⊥ A D$ 于点 $F$ . 若 $A E = 30 d m ， B C =$ $40 d m$ ，一男孩从扶梯走到滑梯的顶部，然后从滑梯滑下，他所经过的总路程是多少(结果保留根号)?

查看试题解析

四、实践探究题

19. 阅读：在平面直角坐标系中，已知两点的坐标，可构造直角三角形，运用勾股定理，求这两点间的距离；在平面直角坐标系中有两点 $A (- 3 ， 5)$ ， $B (1 ， 2)$ ，求 $A$ ， $B$ 两点间的距离 $.$ 过点 $A$ 作 $x$ 轴的垂线，过点 $B$ 作 $y$ 轴的垂线，相交于点 $C$ ，连接 $A B . ∴ A C = | 5 - 2 | = 3$ ， $B C = | 1 - (- 3) | = 4$ ，在 $R t △ A B C$ 中，由勾股定理得： $A B = \sqrt{A C^{2} + B C^{2}} = \sqrt{3^{2} + 4^{2}} = 5$ ，若 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ ，从而得到两点间的距离公式 $M N = \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}} .$ 解决下列问题：

(1)、若 $P (2 ， 4)$ ， $Q (- 3 ， - 8)$ ，则 $P Q$ 两点间的距离 $P Q =$ ；

(2)、如图 $2$ ：点 $D (3 ， 3)$ ，点 $E (5 ， - 1)$ ，则 $D E =$ ，若 $O H ⊥ D E$ ，则 $O H =$ ．

查看试题解析
20. 勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，它不但因证明方法层出不穷吸引着人们，更因为应用广泛而使人着迷．

(1)、应用场景1——在数轴上画出表示无理数的点．如图1，在数轴上找出表示2的点A ，过点A作直线l垂直于OA ，在l上取点B ，使 $A B = 1$ ，以原点O为圆心， $O B$ 为半径作弧，则弧与数轴负半轴的交点C表示的数是；

(2)、应用场景2——解决实际问题．如图2，有一个小朋友拿着一根竹竿要通过一个长方形的门，如果把竹竿竖放就比门高出2尺，斜放就恰好等于门的对角线（ $B D$ ），已知门宽6尺，求竹竿长．

查看试题解析
21. 先阅读材料，然后回答问题：
形如 $\sqrt{a \pm 2 \sqrt{b}}$ 的化简，只要找到两个正数 $x$ 、 $y$ ，使 $x + y = a$ ， $x y = b$ ，

使得 ${(\sqrt{x})}^{2} + {(\sqrt{y})}^{2} = a$ ， $\sqrt{x} \cdot \sqrt{y} = b$ ，

那么则有 $\sqrt{a \pm 2 \sqrt{b}} = \sqrt{{(\sqrt{x} \pm \sqrt{y})}^{2}} = \sqrt{x} \pm \sqrt{y} (x > y)$ ，例如：化简 $\sqrt{6 - 2 \sqrt{5}}$ ， $\sqrt{6 - 2 \sqrt{5}} = \sqrt{5 - 2 \sqrt{5 \times 1} + 1} = \sqrt{{(\sqrt{5})}^{2} - 2 \sqrt{5} \times \sqrt{1} + {(\sqrt{1})}^{2}} = \sqrt{{(\sqrt{5} - \sqrt{1})}^{2}} = \sqrt{5} - 1$ ．

(1)、请根据你从上述材料中得到的启发，化简： $\sqrt{5 - 2 \sqrt{6}} =$ ； $\sqrt{7 + 4 \sqrt{3}} =$ ；

(2)、在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 15 °$ ，其中 $A B$ 边的垂直平分线分别交 $A B$ 、 $B C$ 于点 $D$ 、 $E$ ，当 $A C = 1$ 时，求 $A B$ 的长．（结果要化为最简形式）

查看试题解析

五、综合题

22. 如图，在Rt△ABC中，∠C=90°，

(1)、求作∠BAC的平分线，与BC交于点D（用尺规作图，保留作图痕迹，不写作法）．

(2)、若CD=4，AB=15，求△ABD的面积．

查看试题解析
23. 在Rt△ABC中，∠C=90°，AC=20cm，BC=15cm．现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿线段CB也向点B方向运动．如果点P的速度是4cm/秒，点Q的速度是2cm/秒，它们同时出发，当有一点到达所在线段的端点时，就停止运动，设运动的时间为t秒．求：

(1)、用含t的代数式表示Rt△CPQ的面积S；

(2)、当t=3秒时，P、Q两点之间的距离是多少？

查看试题解析

2023-2024学年初中数学人教版八年级下学期 第十七章 勾股定理 单元测试 A卷

一、选择题

二、填空题

三、解答题

四、实践探究题

五、综合题

2023-2024学年初中数学人教版八年级下学期第十七章勾股定理单元测试 A卷