2023-2024学年初中数学人教版八年级下学期第十六章二次根式单元测试 A卷

试卷更新日期：2024-03-15 类型：单元试卷

进入出卷网下载

一、选择题

1. 下列计算正确的是（）

A、 $\sqrt{16}$ =±4 B、± $\sqrt{9}$ =3 C、 $\sqrt{(- 3)^{2}}$ =-3 D、( $\sqrt{3}$ )²=3

查看试题解析
2. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{30}$ B、 $\sqrt{12}$ C、 $\sqrt{8}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
3. 代数式 $\frac{\sqrt{x + 4}}{x - 2}$ 中x的取值范围是（）

A、x≥-4 B、x>2 C、x≥-4且x≠2 D、x>-4且x≠2

查看试题解析
4. 已知x，y为实数，且 $y = \frac{1}{2} + \sqrt{6 x - 1}$ $+ \sqrt{1 - 6 x} ，$ 则 $\frac{x}{y}$ 的值为（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、2

查看试题解析
5. 下列二次根式中，字母a的取值范围是全体实数的为（）

A、 $\sqrt{a}$ B、 $\sqrt{a - 1}$ C、 $\sqrt{\frac{1}{a + 1}}$ D、 $\sqrt{{(a - 1)}^{2}}$

查看试题解析
6. 下列计算正确的是（）

A、 $4 \sqrt{2} - 2 \sqrt{2} = 2$ B、 $3 \sqrt{3} + 5 \sqrt{2} = 8 \sqrt{5}$ C、 $3 \sqrt{3} \times 2 \sqrt{2} = 6 \sqrt{6}$ D、 $4 \sqrt{2} \div 2 \sqrt{2} = 2 \sqrt{2}$

查看试题解析
7. 下列二次根式中，与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、 $\sqrt{20}$

查看试题解析
8. 下列各式中正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt{x^{2}} = x$ C、 $\sqrt[3]{(- x)^{3}} = - x$ D、 $\sqrt{(- x)^{2}} = - x$

查看试题解析
9. 若 $3 - \sqrt{2}$ 的整数部分为a，小数部分为b，则代数式 $(2 + \sqrt{2} a) \cdot b$ 的值为（）

A、-2 B、0 C、1 D、2

查看试题解析
10. 下列式子：①( $\sqrt{19}$ )²=19；②( $\sqrt{- 19}$ )²=-19；③( $\sqrt{a - b}$ )²=a-b；④a=-( $\sqrt{- a}$ )²(a≤0)．其中一定正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 计算： $\sqrt{3}$ × $\sqrt{5}$ ＝.

查看试题解析
12. 若代数式 $\sqrt{x + 3} + {(x - 2)}^{0}$ 在实数范围内有意义，则x的取值范围是.

查看试题解析
13. 已知 $a ， b$ 为实数，且满足 $\sqrt{a - 8} + \sqrt{8 - a} = b -$ 2 ，则 $\sqrt{a b}$ 的值是.

查看试题解析
14. 实数a，b在数轴上的位置如图所示，化简|a+1|- $\sqrt{(b - 1)^{2}} + \sqrt{(a - b)^{2}}$ = ．

查看试题解析
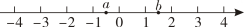15. 将一组数 $\sqrt{3} ， \sqrt{6} ， 3，2 \sqrt{3} ， \sqrt{15} ， \dots ， 3 \sqrt{10}$ 按下面的方式进行排列：
$\sqrt{3 ，} \sqrt{6} ， 3，2 \sqrt{3} ， \sqrt{15} ；$
$3 \sqrt{2} ， \sqrt{2} 1，2 \sqrt{6} ， 3 \sqrt{3 ，} \sqrt{30} ；$
$\dots$
若2 $\sqrt{3}$ 的位置记为(1，4)，2 $\sqrt{6}$ 的位置记为(2，3)，则这组数中最大的数的位置记为.

查看试题解析

三、计算题

16. 计算：

(1)、 $\sqrt{27} + \sqrt{\frac{1}{3}} - \sqrt{12} ，$

(2)、 $(\sqrt{19} + 1) (\sqrt{19} - 1) .$

(3)、 ${(\sqrt{2} + 1)}^{2} + 2 \sqrt{2} (\sqrt{2} - 1) .$

查看试题解析
17. 化简：

(1)、 $\sqrt{1 - 2 x + x^{2}} + \sqrt{x^{2} - 8 x + 16} (1 \leq x < 4)$

(2)、 ${(\sqrt{2 - x})}^{2} - \sqrt{x^{2} - 6 x + 9}$

查看试题解析
18.

(1)、已知x=2+ $\sqrt{3}$ ， y=2- $\sqrt{3}$ ，求 $\frac{x}{y} - \frac{y}{x}$ 的值；

(2)、已知a= $\frac{1}{\sqrt{2} - 1}$ ， b= $\frac{1}{\sqrt{2} + 1}$ ，求a²-3ab+b²的值

查看试题解析

四、解答题

19. 在解决数学问题时，有时信息不太明显，需要结合图形特殊式子成立的条件、实际问题等发现，我们把这样的条件称为隐含条件，所以我们在做题时，要注意发现题目中的隐含条件．
例如：化简( $\sqrt{1 - 3 x}$ )²-|1-x|．
解：由1-3x≥0，得x≤ $\frac{1}{3}$ ， ∴1-x>0，∴原式=(1-3x)-(1-x)=1-3x- 1+x=-2x．
按照上面的解法，试化简： $\sqrt{(x - 3)^{2}} - (\sqrt{2 - x})^{2}$ ．

查看试题解析
20. 某居民小区有一块形状为长方形的绿地ABCD，长方形绿地的长BC为 $\sqrt{243}$ m，宽AB为 $\sqrt{128}$ m，现要在长方形绿地中修建一个长方形花坛(即图中阴影部分)，长方形花坛的长为( $\sqrt{14}$ +1)m，宽为( $\sqrt{14}$ -1)m．

(1)、长方形ABCD的周长是多少？

(2)、除去修建花坛的地方，其他地方全修建成通道，通道上要铺上造价为5元/m²的地砖，要铺完整个通道，则购买地砖需要花费多少元？(结果化为最简二次根式)

查看试题解析

五、实践探究题

21. 先阅读，再解答问题．
恒等变形，是代数式求值的一个很重要的方法，利用恒等变形，可以把无理数运算转化为有理数运算，可以把次数较高的代数式转化为次数较低的代数式．如：当x= $\sqrt{3}$ +1时，求 $\frac{1}{2}$ x³-x²-x+2的值，为解答这题，若直接把x= $\sqrt{3}$ +1代人所求的式中进行计算，显然很麻烦．我们可以通过恒等变形，对本题进行解答．
方法一：将条件变形．由x= $\sqrt{3}$ +1，得x-1= $\sqrt{3}$ ．再把所求的代数式变形为关于(x-1)的表达式．
原式= $\frac{1}{2}$ [x²(x-1)-x(x-1)-3x]+2= $\frac{1}{2}$ [x(x-1)²-3x]+2= $\frac{1}{2}$ (3x-3x)+2=2．
方法二：先将条件化成合适的等式，再把等式两边同时平方，把无理数运算转化为有理数运算．由x-1= $\sqrt{3}$ ，可得x²-2x-2=0，即x²-2x=2，x²=2x+2．
原式= $\frac{1}{2}$ x(2x+2)-x²-x+2=x²+x-x²-x+2=2．
请参照以上解决问题的思路和方法，解决以下问题：

(1)、已知a= $\sqrt{11}$ -1，求a²+2a+2的值；

(2)、已知x=2+ $\sqrt{5}$ ，求x²-4x+200的值；

(3)、已知x=2+ $\sqrt{3}$ ，求 $\frac{x^{4} - x^{3} - 9 x^{2} - 5 x + 5}{x^{2} - 4 x + 2}$ 的值．

查看试题解析
22. 观察下列各式并解答问题：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{2} = 1 \frac{1}{2}$ ；
$\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2} - \frac{1}{3} = 1 \frac{1}{6}$ ；
$\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3} - \frac{1}{4} = 1 \frac{1}{12}$ .

(1)、请你按照上面每个等式反映的规律，写出用n(n为正整数)表示的等式：。

(2)、利用上述规律计算 $\sqrt{\frac{50}{49} + \frac{1}{64}}$

(3)、已知 $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \dots + \sqrt{1 + \frac{1}{(n - 2)^{2}} + \frac{1}{(n - 1)^{2}}} + \sqrt{1 + \frac{1}{(n - 1)^{2}} + \frac{1}{n^{2}}} = n - \frac{1}{2023}$ ，求n的值.

查看试题解析

六、综合题

23. 某同学在解决问题：已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $2 a^{2} - 8 a + 1$ 的值．
他是这样分析与求解的：
先将 $a$ 进行分母有理化，过程如下，
$a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ，
∴ $a = 2 - \sqrt{3}$ ，
∴ $(a - 2)^{2} = 3$ ， $a^{2} - 4 a + 4 = 3$ ，
∴ $a^{2} - 4 a = - 1$ ，
∴ $2 a^{2} - 8 a + 1 = 2 (a^{2} - 4 a) + 1 = 2 \times (- 1) + 1 = - 1$ ．
请你根据上述分析过程，解决如下问题：

(1)、若 $a = \frac{1}{\sqrt{2} - 1}$ ，请将 $a$ 进行分母有理化；

(2)、在（1）的条件下，求 $a^{2} - 2 a$ 的值；

(3)、在（1）的条件下，求 $2 a^{3} - 4 a^{2} - 1$ 的值

查看试题解析

2023-2024学年初中数学人教版八年级下学期 第十六章 二次根式 单元测试 A卷

一、选择题

二、填空题

三、计算题

四、解答题

五、实践探究题

六、综合题

2023-2024学年初中数学人教版八年级下学期第十六章二次根式单元测试 A卷